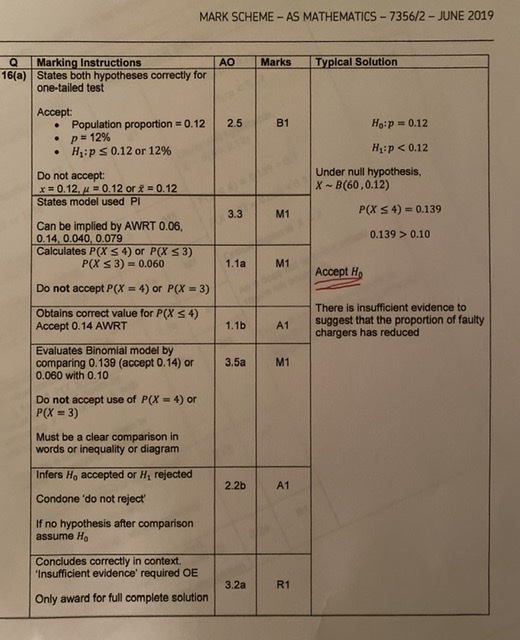
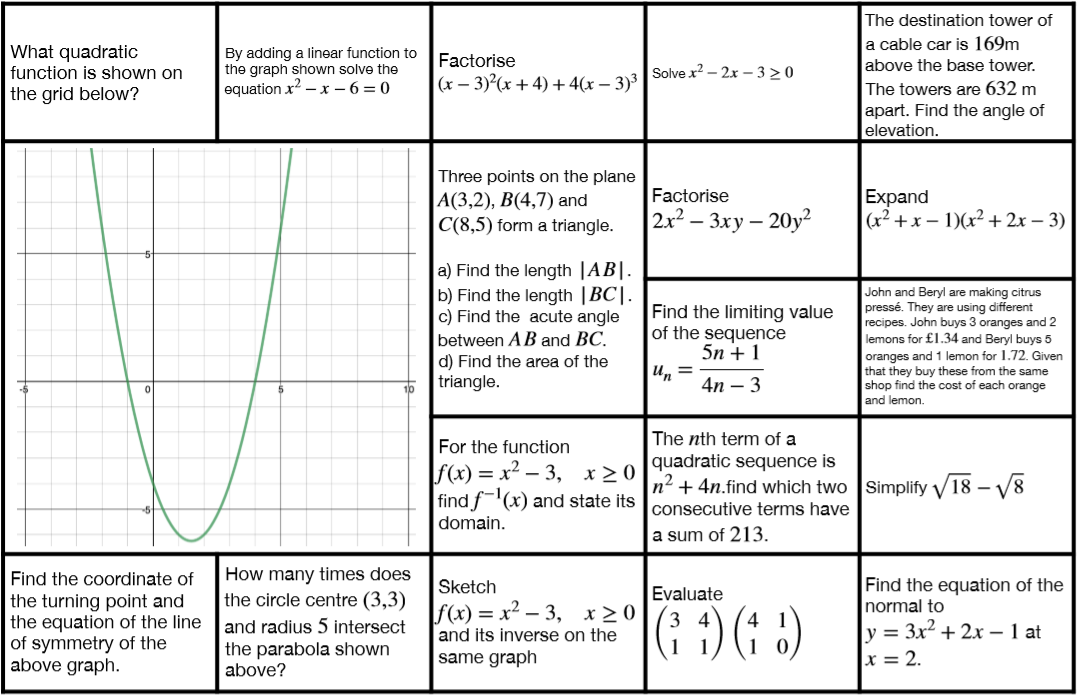
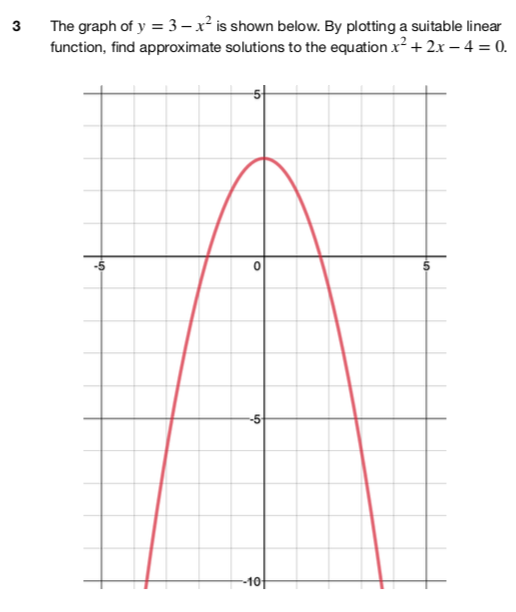
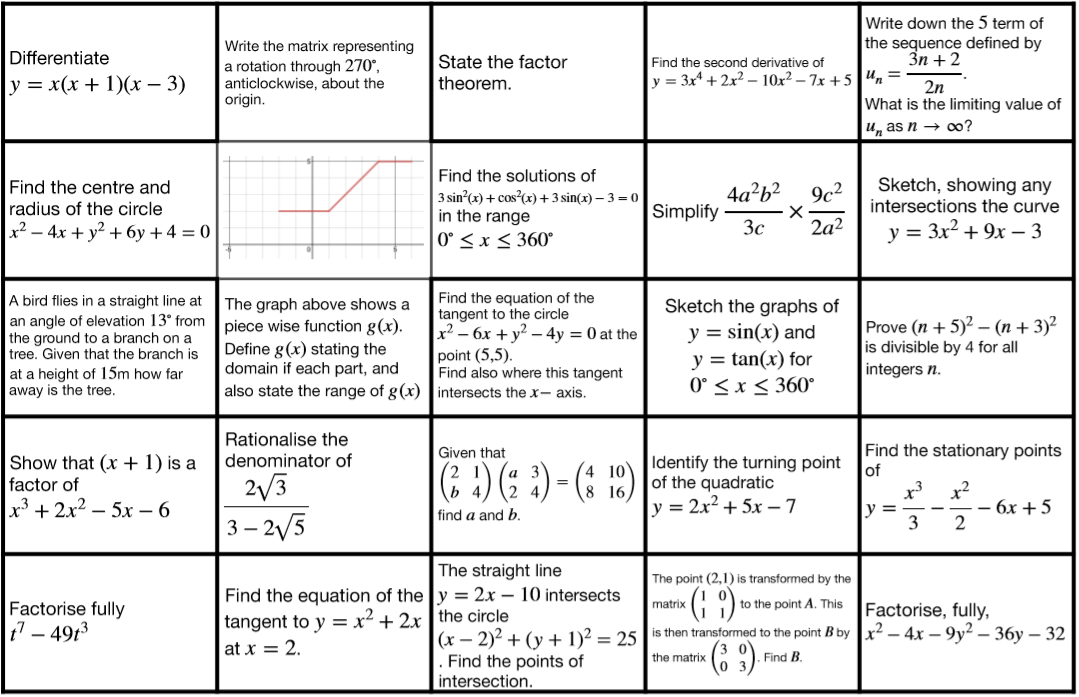
Tonight (7pm UK time, Tuesday 21st January) I am hosting the NCETM #mathscpdchat on the subject of “Using Technology to Enhance A-Level Maths Learning”.
As a prelude to this I am sharing a desmos creation that was heavily inspired by something posted by Steve Phelps (@giohio ) over the Christmas break.
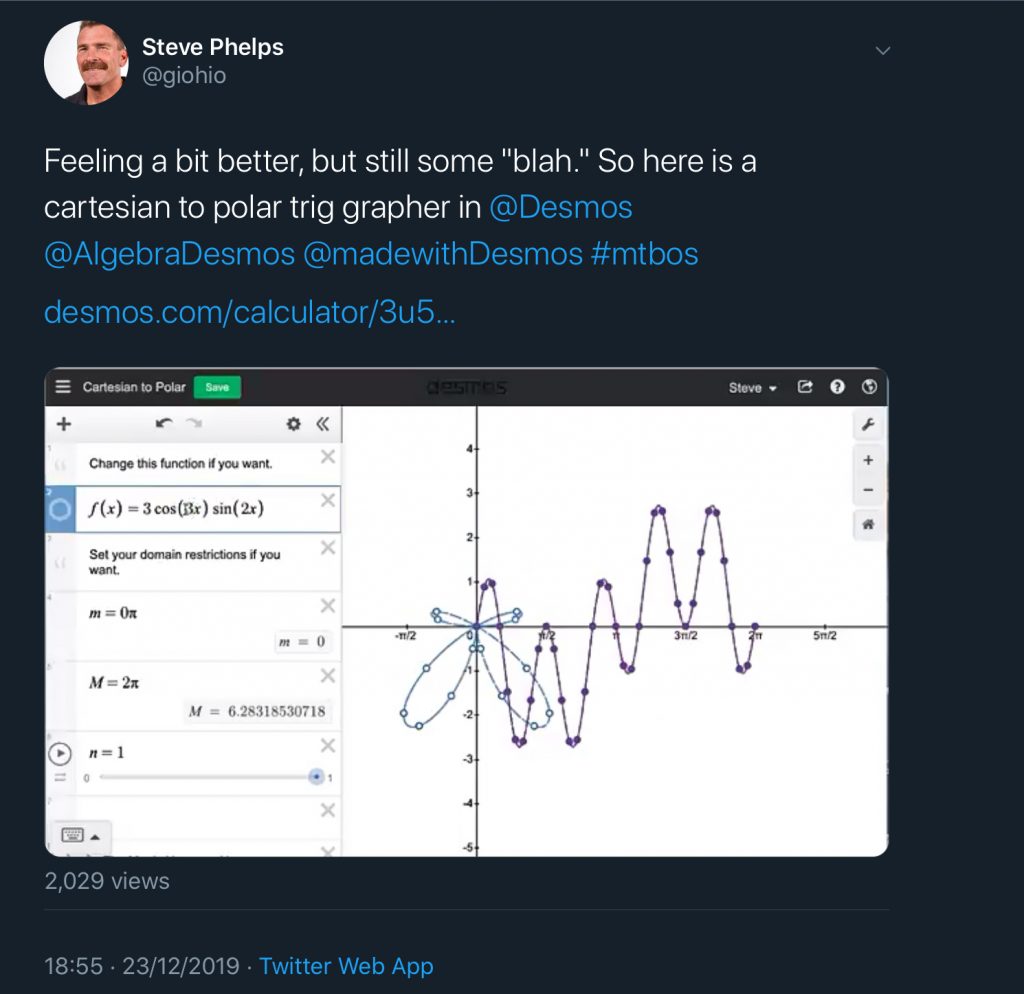
Here is my version that does something slightly different, with a couple of options. It can be found here.
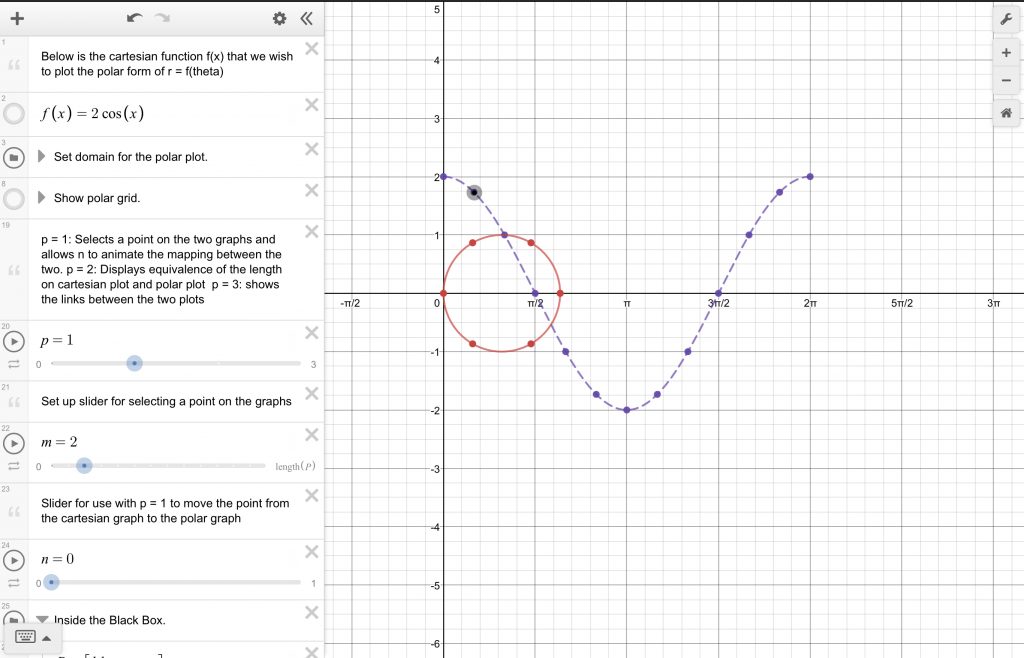
As I’m also pretty passionate about empowering other teachers to create their own versions of things using technology I produced some step-by-step instructions for creating this.
These can be downloaded here.
For discussion tonight I’m interested in starting to look at the following questions:
- Would you use this kind of “interactive” when teaching the sketching of polar curves?
- Could it lead to any misconceptions?
- Do you think this would have a positive impact on student understanding?
- As a teacher would you want to be able to create this kind of interactive?
- Would the skills needed to create this be useful for students to learn?
Please try and join in the discussion tonight….