This post is an expanded version of a review I wrote for the IMA’s (Institute of Mathematics and it’s Applications) magazine Mathematics Today which was published in the December 2015 issue. If you are in the UK ad aren’t already a member of the IMA I really would encourage you to join, the magazine is great and there are some great regional talks etc.
SUMAZE! is an app available for both Apple and Android devices and is a completely free download (and free of adverts).
I first became aware of MEI’s new mathematics game, SUMAZE!, at the beginning of half term after seeing it mentioned on Twitter. It is available for both iOS and Android devices and “awesome puzzle game” is typical of the reviews in these stores. Indeed, SUMAZE has already entered the top 10 educational apps chart in the Google play store despite only being released on the 20th October 2015. Sumaze is based on an idea of Richard Lissaman of MEI and was then developed into the apps we have today.
Soon after downloading, it became obvious that it was going to be very addictive and consume quite a bit of my holiday.
When you start the app you are presented with the following screen:
 At first the differing levels are locked and are opened as you complete more of them.
At first the differing levels are locked and are opened as you complete more of them.
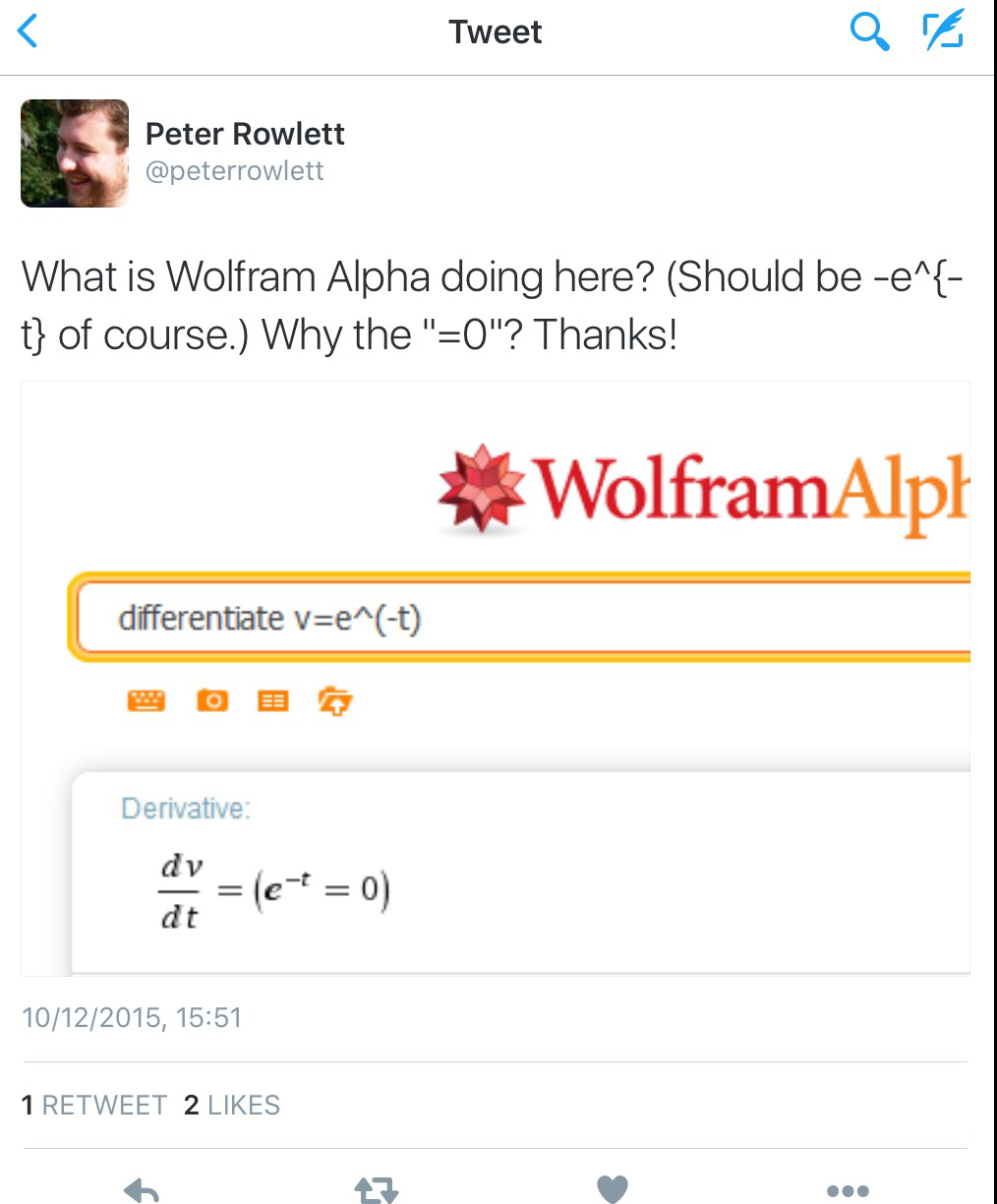
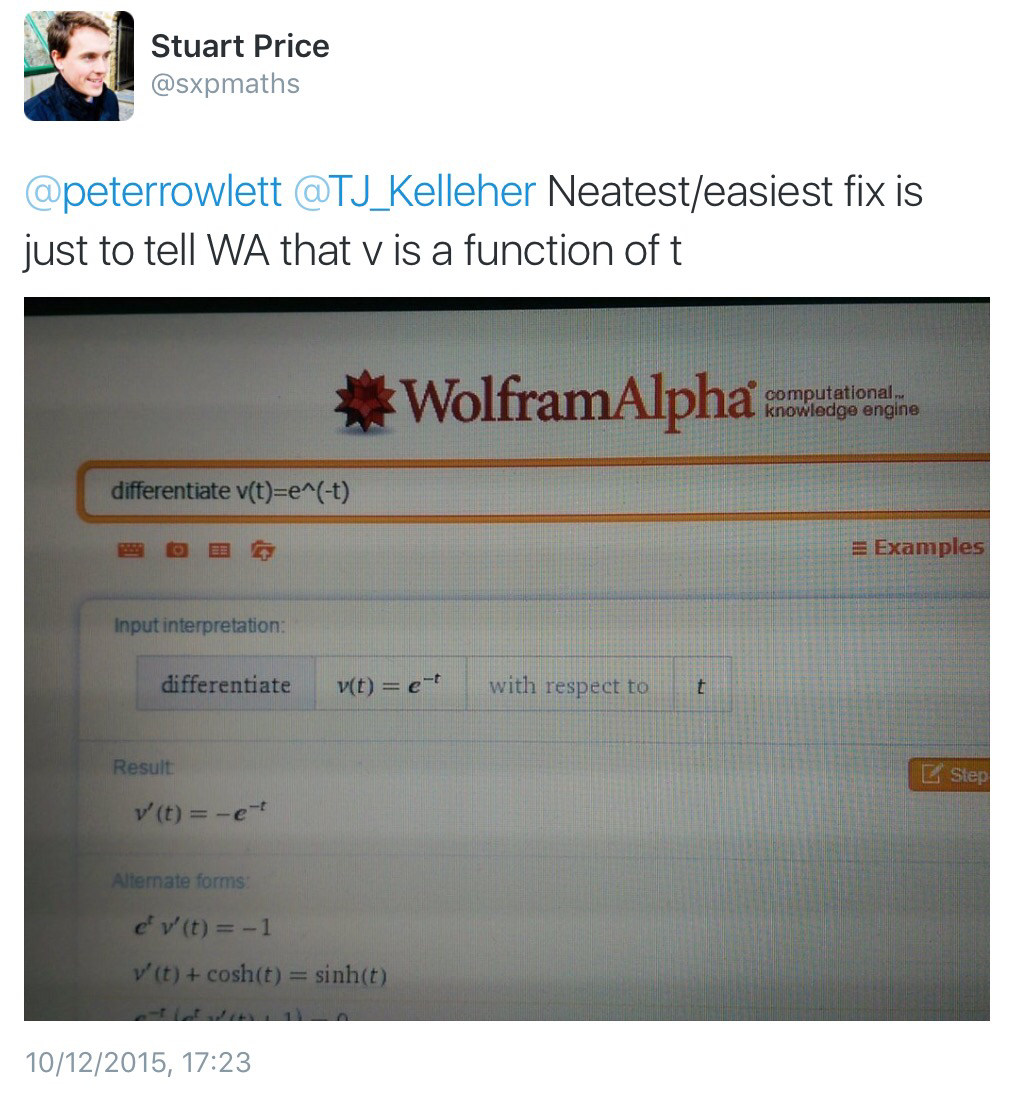
The game is simple in concept; you, as the player, just need to move a numbered block to an exit point. In working your way to the exit however, operator blocks modify the number on your block and green blocks only let you pass if your number satisfies the condition shown. The choice of operators and conditions can make all the difference in how quickly you can complete a level. The app is very well designed, with a slick look and an intuitive interface. Six core topics are covered by the currently available levels (arithmetic, negatives, powers, inequalities and modulus, logarithms and properties of number) and these are unlocked as you complete the levels. Whilst you may think that arithmetic is a simple mathematical concept, in fact some of the levels for each section can be surprisingly (and frustratingly) difficult! I was stuck on a particular level in the Numbers section for what felt like hours and one level in the final “Fermat’s Rooms” seemed very challenging. I like to think that there is a bug in this level concerning modular arithmetic.
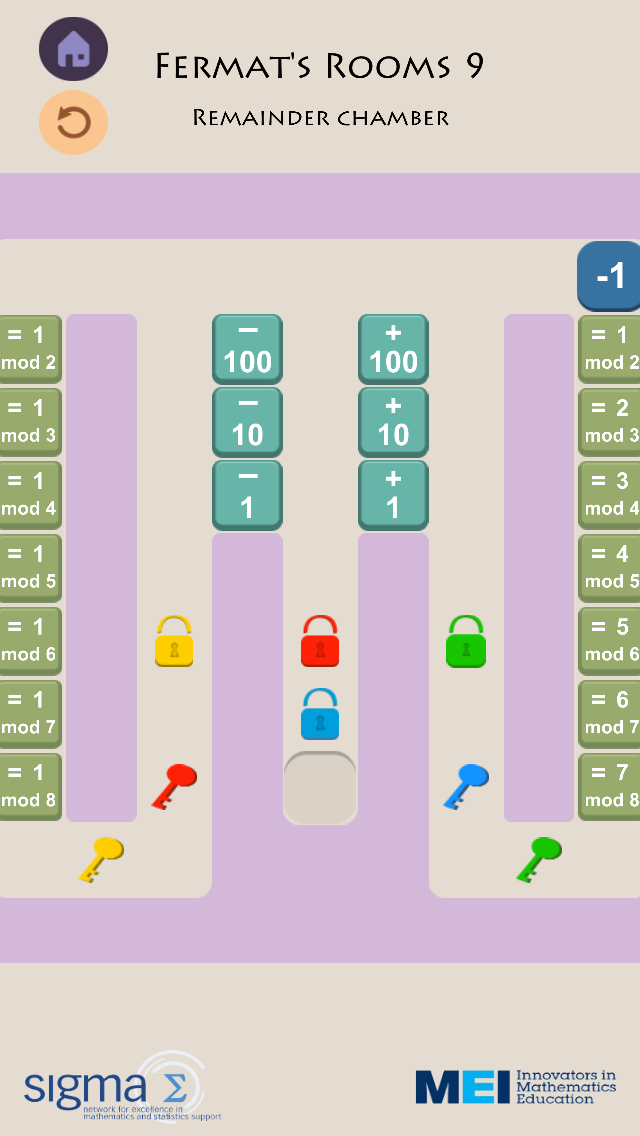
To me -1 should pass through the green condition block labelled “=1 mod 2” and then all the others down the right hand side. However this isn’t allowed and after forming some equations you can obtain a value in the 800s.
These mazes could be a great way for a teacher to introduce the concept of logarithms for example. Students working through the levels will develop a deeper conceptual understanding of what a logarithm “actually is” than they may have achieved through just the definition and some questions. It would be a help if there was a “teacher unlock” code to unlock levels on school devices so that particular levels could be used by the students.
The SUMAZE! puzzles also appear as resources on MEI’s integralmaths.org website for use in class. In addition, since writing the review for the IMA a web version has been made publicly available.\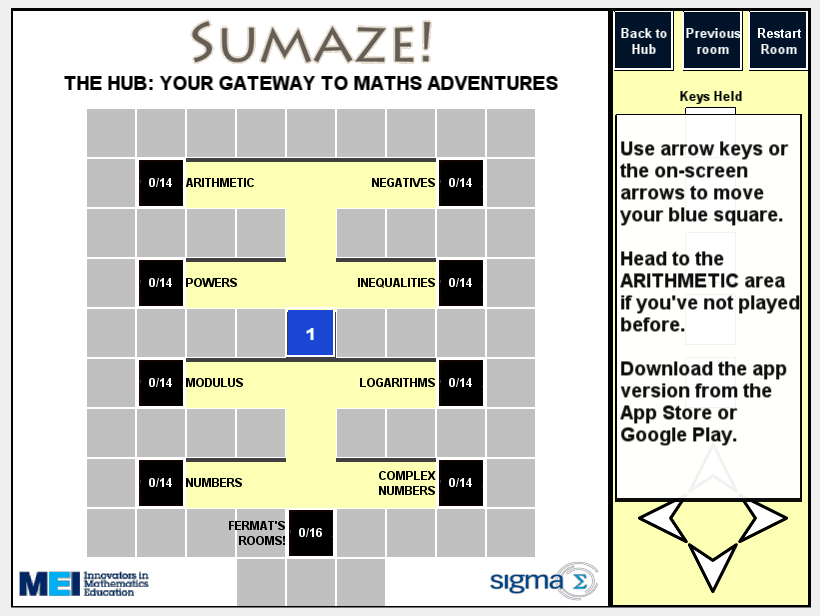
In the web version all levels are unlocked and so can be used to introduce students to logarithms for example. I used this web app with a Year 7 class towards the end of the year, instructing them to do the arithmetic levels first and then allowed them to select between negatives, powers or modulus. A lot of them chose to try the modulus levels as this was something unfamiliar to them. It was really nice to watch them learn about the modulus function (a topic that they definitely wouldn’t normally come across at such an age) and be self motivated to do so.
I really hope that MEI produce some add-on levels for this game as I am now left wanting more! Similar apps for other topics would also be great, I can think of similar ideas that would be good for both younger and older target audiences.
As an aside, does anyone know who the “Dr H” some of the levels refer to is? I think I am missing some popular culture reference…..
I’ll end the review with a quote sent to me from Richard Lissaman that he had received from a user of the app
“It happened that I was visiting with my 15-year-old grand-daughter this afternoon and mentioned the Sumaze! app. This girl is something of a mathophobe, but no sooner had I mentioned the app than she downloaded it to her iPad. Then it was all that I could do to pry it away from her to talk about adding rational functions. Thanks so much for telling me about this”
If you haven’t already succumbed to this game, download it now, I promise that you will enjoy it.