Month: July 2015

Yesterday’s post was a bit mammoth, so today’s post is much shorter! I’m sure you are all releived by this. 

Back in April I posted on my Mathematical Journey and in that post I mentioned how I felt lucky to have a granny who was a maths teacher. 

Ever since I can remember she would talk about maths with me, set me problems to do and send me coded messages in the post. As she taught at the Royal College for the blind this included teaching me Braille which sadly I can no longer remember. Whilst sorting through some stuff last night I found some old letters etc so thought I would share a photo here 

 
My handwriting hasn’t really improved much since then to be honest. 

So, here is issue 88 of the Math(s) Teachers at Play blog carnival. This acts as a round up of some cool blog posts that have been published since issue 87 over at cavmaths. As usual people have submitted entries, which I will supplement with some posts that I have really enjoyed reading in the last few weeks.

It is tradition for the post to start with something about the issue number so here goes!

Firstly, here are a few calculations that result in 88 (taken from Zoo of Numbers

\( \begin{align} 88 &= 23^2 – 21^2 \\ &= 13^2 – 9^2 \\ &= 4^2+6^2+6^2 \\ &= 2^3+2^3+2^3+4^3 \\ &= 3+4+5+6+7+8+9+10+11+12+13 \\ &= 17+ 19 + 23+29 \end{align} \)

88 is also an Erdos-Woods number. An Erdos-Woods number, \(k\) is defined to be the length of a chain of numbers \(n,(n+1),(n+2), \cdots + (n+k)\) such that each integer \(n+i\) for \(0<i<k\) shares at least one prime factor with either \(n\) or \(n+k\).16 is an Erdos-Woods number because for each number in the chain

\(2184,2185, \cdots, 2199,2200\)

shares at least one factor with either \(2184\) or \(2200\). TheErdos-Woods numbers are sequence A059756 in the Online Encyclopedia of Integer Sequences, the first few are as follows

\(16,22,34,36,46,56,64,66,70,76,78,86,88,92,94,96,100 \)

I am now wondering if there is a nice way to compute Erdos-Woods numbers, yet another thing to look at when I get the chance…

Right, I had some really interesting submissions this month.

Jo Morgan (@mathsjem) shared this great post about Teaching Foundation GCSE (Grades 9 and 10 in the States) classes. This is one of her most popular posts of all time, and it contains some great tips for engaging those students who really struggle at maths – I know I will be returning to it when I am teaching Foundation GCSE.

Lisa (I can’t find her on Twitter unfortunately) shared an article she has written for the Huffington Post titled “Reconsidering Math as an Art Form”. It was inspired by Paul Lockhart’s essay a “Mathematician’s Lament”. I agree with Lisa and think this should be essential reading for mathematics educators. I particularly liked his comparison of the teaching of Mathematics to the teaching of music – I fundamentally believe mathematics is as creative as any of the creative arts and it is a massive shame that a lot of school children don’t see this side of maths.

Stephen Cavadino (@srcav) shared this amusing post linking a “Quirk of Probability” to a mobile game. I really enjoyed reading this before I received the submissions, and it was nice to be reminded of it.

April Freeman (who blogs here) has a post about using bundles of popsicle (or ice lolly sticks) to help with the understanding of place value for her daughter. I think this could be a useful technique to help with the visualisation of place value.

This nice review of a year of running a maths club for 4th and 5th graders by Benjamin Leis is well worth a read, there are some great tips that are applicable to general teachers as well as those running extra-curricular clubs. The Yearly Topics Map on his blog also contains links to some really nice resources.

Mrs E (@MrsETeachesMath) has shared this fairly short post on introducing proof. Proof is always a topic that is relatively challenging to teach. The ordering a story idea is a nice analogy to emphasise the importance of logical thinking when completing a mathematical proof.

Christy (@housefulofchaos) is a homeschooler based in Ontario and she submitted this on “Minecraft Multiplication Practice”. I confess I’ve never played Minecraft, but I am now very intrigued by this detailed post on a way to make multiplication more interesting. I’m also very curious about the online course she is running on Minecraft Maths, I wonder if I would be allowed to join?!?

Pea has shared a post on using concrete manipulative to teach the addition of fractions. Too often addition of fractions seems to be based on rote learning and I like how the understanding is at the fore-front of this approach, and I like the fraction discs.

Denise Gaskins (@letsplaymath), the organiser of this carnival has shared this fantastic post on introducing infinite series to children  with a puzzle courtesy of Don Cohen and an additional puzzle for older children from James Tanton. The infinite series approach to the solution of James Tanton’s puzzle is amazing, and I certainly don’t think I would have come up with it – I used similar triangles! I hadn’t seen Don Cohen’s “Map of Calculus for Young People” before, or looked at Don Cohen’s site; I’ll be spending more time here!

The final submission comes from Manan (@shahlock) who has shared his comic for Pi approximation day. I love Manan’s comics, make sure you check out the others.

I came across this site examining the maths of banknote patterns, it is a really interesting read. I had n’t really considered the mathematics behind these patterns and I will certainly be exploring them more in the future. I came across this article thanks to Colin Beveridge (@icecolbeveridge) who tweeted it alongside this Desmos sheet . Colin has also recently shared his Mathematical Journey (in response to this post of mine), it is a really interesting read, and contains some useful advice for any budding mathematician.

Danny Brown (@dannytybrown) has, in the last couple of days shared this long post about mathematical teaching styles. I promise it is worth spending time to read to the end!!! Get involved in the conversation about it on Twitter to.

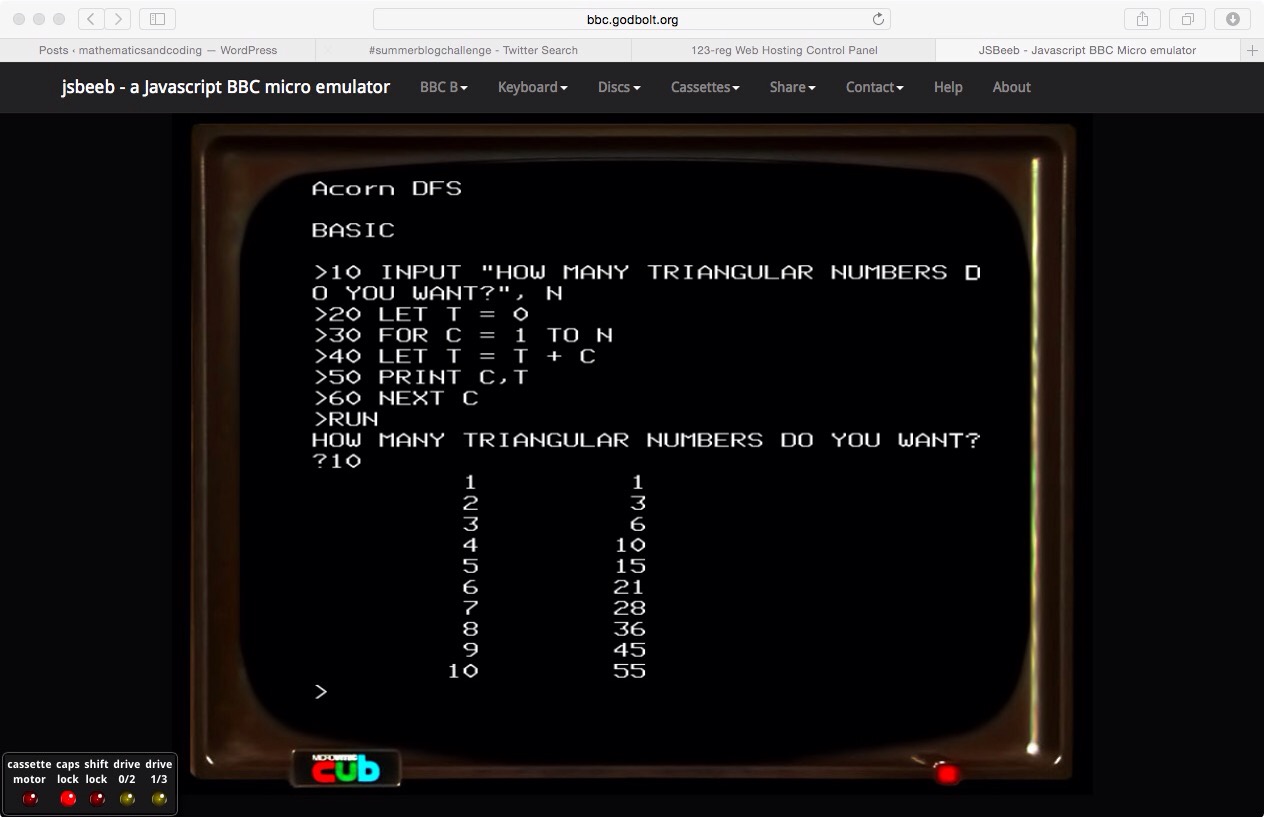
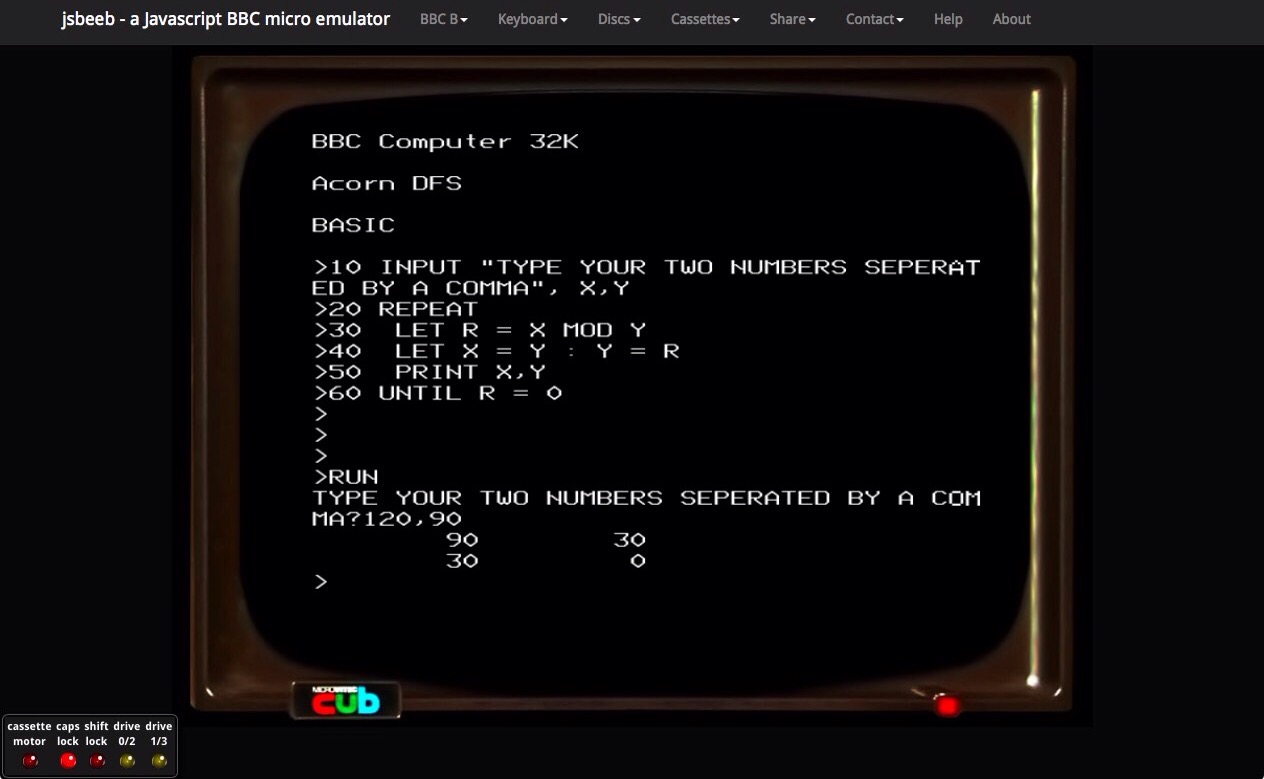
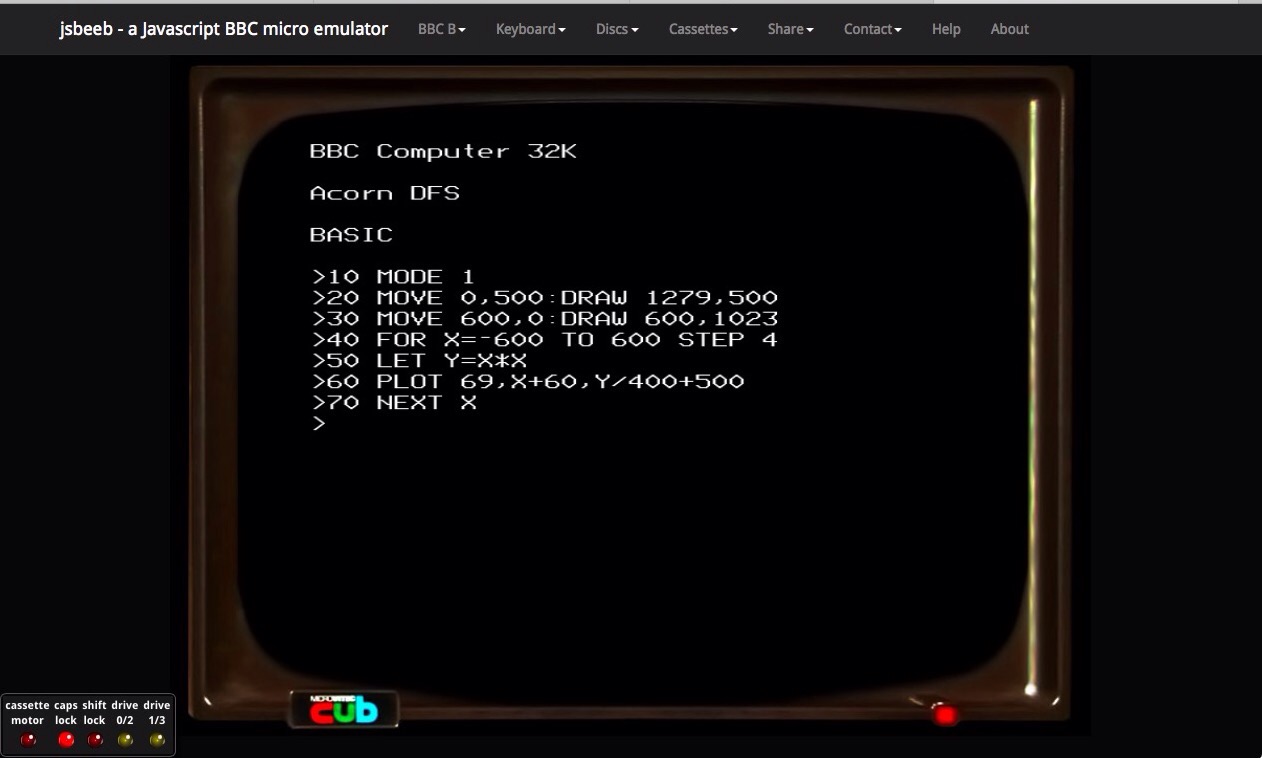
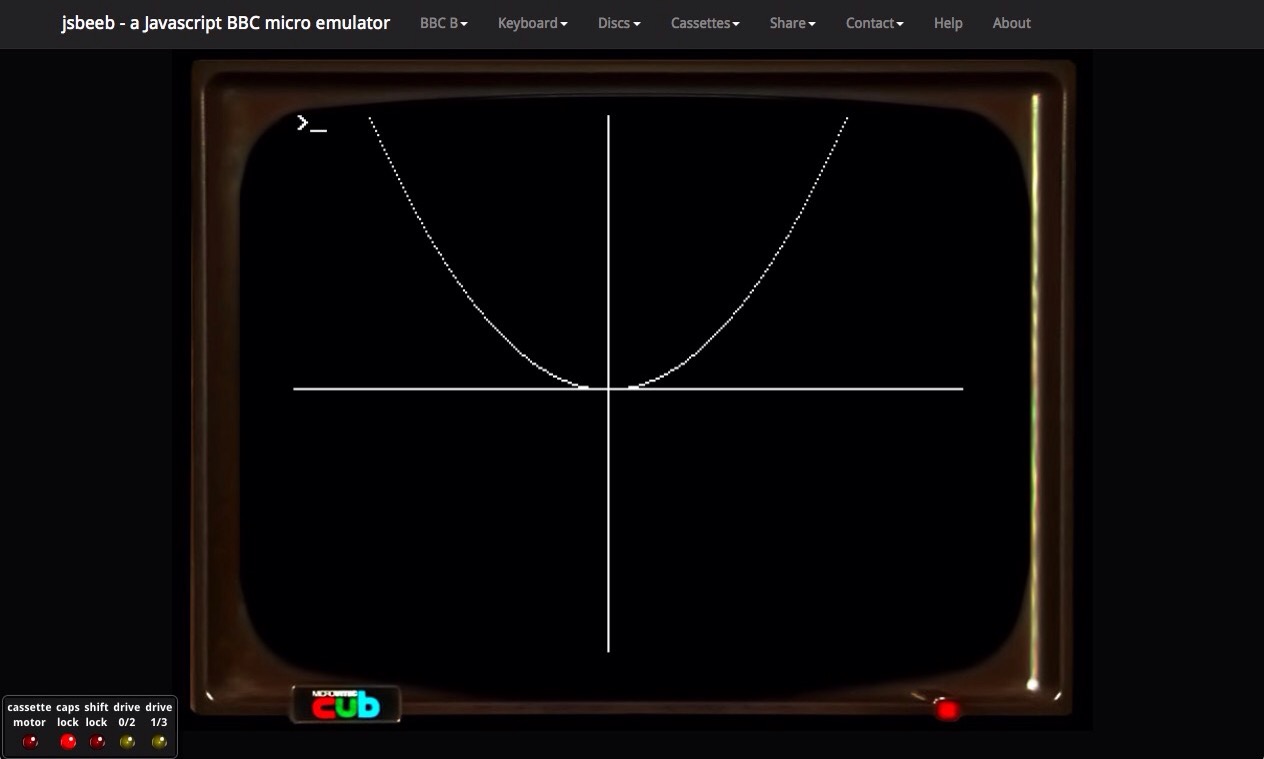
Because of my background I am very interested in computer programming and the benefits this can bring to mathematics education. I have been looking at some early programs designed to be used in the maths classroom for the BBC Micro and have discovered an emulator by Matt Godbolt (@mattgodbolt), he has a video describing the coding of this available here.

Finally a few of us our taking part in a challenge to write a blog post every day of the summer holiday, the index is available here. At the moment it is me, Christine Norledge (@MissNorledge), Kim Thomas-Lee (@kimThomasLee), Mark Wilson (@mwimaths), Archbishop Sancroft High School maths department (@ASHS_Maths), @funASDteacher and Jennifer Stice (@mathchick5) taking part. We would love you to take a look t our posts and maybe join us in the challenge?

The next edition of this blog carnival will be at Mrs E Teaches Math.

At the beginning of July Stuart Price (@sxpmaths) blogged this post looking at A Level textbooks through the ages.  I really enjoyed reading this, and was particularly drawn to a picture of a book that described computer programs written in Basic for use in the maths classroom. I was so keen to look at this that I straight away ordered a copy from Amazon and here it is:

  
This book is fantastic, and it’s a shame that I don’t know of anything similar today (does anyone reading this?) – cue for me to write one, yet another project….

The BBC Micro holds a special place in my heart as it is the first computer that I can remember using at Grove Primary School. I remember sitting at one in the BBC room and doing various things, including my first bit of programming in BASIC (I later had a fairly long hiatus before coming back to coding).

Having become used to modern computers you forget the limitations of older computers such as the BBC Micro. For example, at the beginning of the book some of these limitations are mentioned, such as the fact that the BBC Micro’s filing system can only cope with 31 filenames. I particularly like this quote from the introduction to the book

“The lack of ‘idiot-proofing’ means that they [the programs] may sometimes ‘crash’, but in these circumstances a consideration of why it went wrong may itself be very illuminating, This will usually be due to inaccuracies in computer floating-point arithmetic, the non-existence of solutions, or the singularities of functions, all of which children should be aware of.

I don’t know of many ‘children’ who have an understanding of floating-point arithmetic or the failure of certain numerical methods in the presence of singularities – it is even possible to get through some undergraduate numerics courses without really tackling these issues!

I am going to write a few posts over the summer looking at some of the programs in this book, with the odd modification (I’ve quite enjoyed doing a bit of Basic for the first time in over 20 years).

Of course, to run some BBC Basic programs I either need access to  BBC Micro (If anyone has a working one that they don’t want anymore please let me know!!) or a decent emulator. As a mac user there aren’t many BBC emulators available, and those that are don’t seem to have been maintained since 2012. But then I found this excellent Javascript emulator by Matt Godbolt (@mattgodbolt). On his blog there is a lot more detail about the implementation of the emulator, as well as some other cool posts – I urge you to check them out if you are interested in coding! The video about the BBC emulator is definitely worth a watch. It’s sad that the emulator doesn’t apper to work on an iPad though.

I first tried Program 1 from the book, which is a simple program to compute the first \(n\) triangke numbers, where \(n\) is an input from the user. This is shown on the screen shot below: 

 I then thought I would try the highest common factor program: 

 I then thought I would look at something a bit more complicated, and try plotting the graph of \( y = x^2 \). One thing that you don’t have to do with things like scaling the output explicitly to fit the graph onto the display when using Matlab or NumPy. Of course the BBC Micro and BBC Basic is not as sophisticated as this, and we are explicitly giving coordinates on the screen of where to colour a pixel – because of this osome scaling needs to be done. This explains the divide by a 400 on line 60 of the below code from the book.  

This code generates the following output which is recognisably the curve of \(y=x^2\) 

 I’m going to play a bit more with the graphics commands and will post next week with some further programs from this book, and maybe one that I have written myself too.

Firstly, put the evening of Monday 24th August into your calendars!!

Thank you to everyone who voted for our first journal article. Around 50 people made a selection and the overwhelming winner was the article “A Glimpse into Secondary Student’s Understanding of Functions” from the journal International Journal for Mathematics Teaching and Learning published online by the Center for Innovation in Mathematics Teaching of the University of Plymouth. 

We will be discussing this at 8pm on the 24th August 2015 – you can follow the conversation using the hashtag #mathsjournalclub. If you can’t make the actual conversation but have read the paper it would be great if you could still contribute some thoughts under the hashtag #mathsjournalclub and they can be used to guide the discussion.

To remind you of the topic of the paper I have included a shot of the first page below. Please click on the link to download the full paper. I will publish some discussion themes about a week before the 24th.

  
I’m really looking forward to discussing this with you all on the 24th.

Math’s seems to be quite popular in the media at the moment, with three great articles printed in the last week or so! I thought I would share them here and provide a short commentary.

The Singular Mind of Terry Tao

The New York Times has published this great (long) article on the life of Field’s Medalist Terence Tao by Gareth Cook (GarethIdeas) The New York Times often seems to publish these kind of long articles, and luckily they have a policy of letting you read 10 articles a month from their website for free! 

I think this article nicely describes the life of a research mathematician, and I particularly like this quote

“The steady state of mathematical research is to be completely stuck. It is a process that Charles Fefferman of Princeton, himself a onetime math prodigy turned Fields medalist, likens to ‘‘playing chess with the devil.’’…”

The article is a very readable account of what it is to be a modern research mathematician, and in it Steven Strogatz sums up maths as a “… conversation with each other over the millennia”, emphasising the connections with mathematical discoveries across the generations.

The New York Times also has a puzzle from Terence Tao here.

John Horton Conway: The Worlds Most Charismatic Mathematician

This article by Siobhan Roberts appeared in the Guardian on Thursday 23rd July is an interesting portrait of the mathematician that Sir Michael Attiyah describes as the “most magical mathematician in the world”. John Conway is famous for his work in the 1970s on symmetry groups. I didn’t realise his commitment to maths education and how much time he spends at maths camps in the university holidays – not many academics would be willing to give up this precious research time. Conway is of course famou for inventing The Game of Life – I will write about this in the future I think, once I have coded it in Python.

This article is fascinating and well worth a read – I will definitely be buying the full book hen it comes out in September.

20 Mathematicians Who Changed the World

Walter Hickey has written this article for Business Insider. It is considerably shorter than the previous two and provides brief (a few lines) information on twenty famous mathematicians. I don’t completely agree with his choices – for instance what about George Boole?!? Who do you think is missing from this list? I’d be interested to know…

The Arithmetic Mean – Geometric Mean (AM-GM) inequality is possibly one of my favourite inequalities (another is the Cauchy-Schwarz inequality, see a later #summerblogchallenge post for more details on this).

Earlier this week I was honoured to have received an envelope of goodies from Ed (@solvemymaths). Alongside the very cool mathematical Mr Men stickers, there was a note from Ed with a lovely geometric illustration of the AM-GM for two lengths \(a,b\).

  In words, the AM-GM inequality states that the arithmetic mean of a set of (non-negative) numbers is always greater than or equal to the geometric mean of the set of numbers. More formally, the AM-GM inequality can be stated as follows: For a set of non-negative real numbers \(a_1,a_2,a_3,…,a_n\) the following inequality holds

 \(\frac{a_{1}+a_{2}+a_{3}+ \cdots  + a_{n}}{n} \geq \sqrt[n]{a_{1}a_{2}a_{3} \cdots a_{n}} \)

Example: For the set \(1,6,9,15\) the arithmetic mean is \(\frac{31}{4} = 7.75\) and the geometric mean is \(\sqrt[4]{810} \approx 5.3348 [\latex].

Proof: There are many different proofs of the AM-GM inequality. The excellent Art of Problem Solving website lists a few here . I particularly like the one using the rearrangement inequality as it is so concise.

The AM-GM inequality is often useful for questions on STEP and Maths Challenge papers, here is a typical question and a solution.

Question: Given that [latex]a,b,c\) are non-negative integers, show that

\((a+b)(b+c)(a+c) \geq 8abc\)

Solution: Given that \(a,b\) then applying the AM-GM inequality we have that

\(\begin{align} \frac{a+b}{2} &\geq \sqrt{ab} \\ a+b &\geq 2\sqrt{ab} \end{align} \)

Performing similar calculations with the other pairings we can obtain

\( \begin{align} b + c &\geq 2\sqrt{bc} \\ a+c &\geq \sqrt{ac} \end{align} \)

So, since the numbers involved are all positive we can multiply the inequalities to obtain

\( \begin{align} (a+b)(b+c)(a+c) &\geq 2\sqrt{ab}2\sqrt{bc}2\sqrt{ac} \\ &= 8\sqrt{abbcac} \\ &= 8\sqrt{a^2b^2c^2} \\ &=8abc \end{align} \)

as desired.

Can you come up with a nicer solution? Can you come up with similar questions?

The AM-GM inequality comes up in higher level maths too, a friend, Edward Hall of the University of Leicester has reminded me that it is used in a modified form when proving the continuous stability of the solutions to parabolic PDEs. He also mentioned that he has recently seen it used in a paper concerning Discontinuous Galerkin (more on these in the future) methods for quasilinear PDEs.

So here is the first of my 47 (if I can count….) blog posts as part of #summerblogchallenge – not quite as many as @MissNorledge!

I thought I would briefly write about rational functions which often come up in A Level and STEP papers. A rational function is any function \(y = f(x) = \frac{P(x)}{Q(x)} \) with \(P(x), Q(x) \) polynomials. Quite often you are asked to sketch such a function. To do this, the normal steps are to find the roots, i.e. where the function crosses the \(x-\)axis which is easily done by solving \(P(x) = 0 \). Then we can think about asymototes: For the horizontal asymptote consider the ratio of the leading coefficients of \(P(x)\) and \(Q(x)\), for the vertical asymptotes try to factorise \(Q(x)\) and find what values make \(Q(x)\) zero. It is the normal to mark on any local maxima and minima. Of course the usual way is to use calculus and differentiate, setting to zero and solving. However, sometimes we just need to know the approximate location of the maxima and minima  and the associated y values. This is due to the fact that we can often sketch the graph using this knowledge and examining what happens near the asymptotes.

I was shown this by another teacher who recently retired and had never considered it before, always using calculus. But with practise, this could be done mentally, pretty quickly I think.

The picture below shows the method for an example. Essentially you imagine a fixed horizontal line across the graph of your rational function, so \(y\) takes on a fixed value. We can then form a quadratic whose coefficients depend on \(y\). A maximum (or minimum) of our rational function will occur when the discriminant of our resulting quadratic is zero. Using this fact we can find the local maximum and minimum values of the rational function.

   

This post will be updated daily to reflect the latest posts that have been published. Anyone who is taking part in the #summerblogchallenge will have their posts listed here – as long as you use the hashtag #summerblogchallenge they will be picked up by me and @MissNorledge and indexed so everyone’s posts can be easily found.

My Posts (@DrBennison)

1. What is #sumerblogchallenge
2. Day 1 – Rational Functions
3. Day 2 – Restaurant Menus
4. Day 3 – AM-GM Inequality
5. Day 4 – Maths in the Media
6. Day 5 – The First #mathsjournalclub Article and Discussion Date
7. Day 7 – The Magic of the Micro: Part 1
8. Day 8 – Math(s) Teachers at Play 88
9. Day 9 – A Bit of Nostalgia
10. Day 10 – The Importance of Having a Break
11. Day 11 – My Twitter History
12. Bonus Post – My WordPress Anniversary
13. Day 12 – One of my Favourite Resources
14. Day 13 – An FMSP Extension Resource
15.  Day 14 – Barnsley’s Fern
16. Day 15 – Summer Further Mathematics Taster Questions
17. Day 16 – A Little Rant about Flash
18. Day 17 – A Few Thoughts on Negative Numbers
19. Day 18 – An Interesting Question from OCR
20. Day 19 – Calculators
21. Day 20 – Further Maths Taster Session for Year 10
22. Day 21 – FMSP Favourite Problems Number 3
23. Day 22 – A Picture of Tea
24. Day 23 – The Damn Quotient Rule
25. Day 24 – Very Short Introductions: Book Review 1
26. Day 25 – Whitstable Maths
27. Day 26 – One Week Till #mathsjournalclub
28. Day 27 – Parental Anxiety with Mathematics
29. Day 28 – For the Love of Books
30. Day 29 – A MathsJam Puzzle
31. Day 30 – Engaging with Academia
32. Day 31 – An Awful MyMaths Homework Question
33. Day 32 – A Bit More on Barnsley’s Fern
34. Day 33 – #mathsjournalcub TONIGHT!!
35. Day 34 – The First #mathsjournalclub Discussion
36. Day 35 – Anscombe’s Quartet
37. Day 36 – Timetable2calendar
38. Day 37 – Making an M1 Paper Harder
39. Day 38 – ZSL London and its Architecture
40. Day 39 – Twitter Chats
41. Day 40 – #mathsjournalclub Second Poll
42. Day 41 – Mathematicians’ Quote Posters
43. Day 42 – Suko
44. Day 43 – No Plan Starters
45. Day 44 – Further Maths Specification Mapping
46. Day 45 – Proof School
47. Day 46 – A VideoScribe Video

Christine Norledge (@MissNorledge)

1. 2015 #summerblogchallenge
2. Day 1 – 51 Days of Summer, The Blogpost Challenge and a Bit of Self Assessment
3. Day 2 – Lessons Learned Writing a Scheme of Work
4. Day 3 – Logarithmic Thinking, Evolution and Dinosaurs
5. Day 4 – Planning for GCSE 2015
6. Day 5 – How Does Bob Marley Like His Maths?
7. Day 6 – Quantity not Quality
8. Day 7 – Looking Back,Looking Forward
9. Day 8 – Exponential Growth and the Chessboard Problem
10. Day 9 – Pick of Twitter 26/07/15
11. Day 10 – the Importance of Trust
12. Day 11 – And Your Starter for Ten
13. Day 12 -Something Old, Something New
14. Day 13 – How to Bend Space and Time – The Joys of Twuffer
15.  Day 14 – The New Sudoku
16. Day 15 – It’s Only a Model…
17. Day 16 – It’s Only a Model – Part 2
18. Day 17 – My #summer10
19. Day 18 – My Twitter History
20. Day 19 – It’s a Marathon not a Sprint
21. Day 20 – Top 5 for Starters
22. Day 21 – Chinese School and the Photo Challenge
23. Day 22 – Photo Challenge (1) Infinite Mirrors
24. Day 23 – Photo Challenge (3) – Arches
25. Day 24 – Photo Challenge (3) Set with Playing Cards
26. Day 25 – Photo Challenge (4) It’s all Greek to Me
27. Day 26 – Photo Challenge (5) – Tiling Patterns
28. Day 27 – Photo Challenge (6) Triangular Bridge
29. Day 28 – Photo Challenge (7) More Arches in Ancona
30. Day 29 – I’m Back
31. Day 30 – Pick of Twitter 16/08/15
32. Day 31 – If This, What Next?
33. Day 32 – I’m Going Again…. (And Facebook)
34. Day 33 – Top 5 for Rich Tasks and Problem Solving
35. Day 34 – Top 5 for Worksheets
36. Day 35 – My Journey into Teaching
37. Day 36 – To 5 Stationary Must Haves
38. Day 37 – Miss, Do You Enjoy Teaching?
39. Day 38 – Pick of Twitter 24/08/15
40. Day 39 – An IFTTT and Pocket Update
41. Day 40 – Three New Blogs
42. Day 41 – Six Good Comics and One Good Thing
43. Day 42 – An Intriguing Use of Primes
44. Day 43 – Google Trends
45. Day 44 – Pick of Twitter 30/08/15
46. Day 45 – My #summer 10 Revisited
47. Day 46 – My Classroom, Part 1
48. Day 47 – Display Goodies
49. Day 48 – Command Word Posters
50. Day 49 – Back to School Essentials
51. Day 50 – Useful Things for Website Developers
52. Day 51 – (Almost) Failing at the Final Hurdle

Mark Wilson (@mwimaths)

1. Day 1 – Psyching Myself Up
2. Day 2 – Circle Theorem Toolkit
3. Day 3 – In Praise of Teacher Led Inset
4. Day 4 – Google Keep as a Task Management Tool
5. Day 5 – Mix It Up: A Group Work Strategy
6. Day 6 – Transitioning to BYOD
7. Day 7 – Time Management Video
8. Day 8 – The Digital Native
9. Day 9 – Digital Card Sorts
10. Day 10 – Assignment Workflow
11. Day 11 – Revision Carousel
12. Day 12 – I Didn’t Want to do Maths
13. Day 13 – Google Search Takeaways
14. Day 14 – Fermi Questions
15. Day 15 – Stand Off
16. Day 16 – Set Theory Extension
17. Day 17 – Book Marking
18. Day 18 – Fermi Questions: A Worked Example
19. Day 19 – Taking Sabbaths
20. Day 20: Statistical Stories
21. Day 21 – BYOD: Some Tools
22. Day 22 – Subtracting From Questions
23. Day 23 – Who’s Studying Further Maths?
24. Day 24 – Teaching Google Sheets
25. Day 25 – Incognito Mode
26. Day 26 – Sunday Sabbatical: Podcasts
27. Day 27 – The 5 Minute Lecture
28. Day 28 – Homework, Feedback and Forms
29. Day 29 – docAppender and Keeping in the Loop
30. Day 30 – Don’t Watch the News Today
31. Day 31 – Multistep Chains
32. Day 32 – Set Zero: An Appeal
33. Day 33 – Sunday Sabbaticals: Mathematical Pilgrimages
34. Day 34 – Doctopus and Homework Feedback
35. Day 35 – Classroom and Calendars
36. Day 36 – Loop and the Introduction to Mechanics
37. Day 37 – Analysing the Answers
38. Day 38 – In Defense of Rote
39. Day 39 – Keeping Track Using VLOOKUP
40. Day 40 – Sunday Sabbaticals: xkcd
41. Day 41 – Farewell to the #summerblogchallenge

Archbishop Sancroft High School Maths Department (@ASHS_Maths)

1. Day 1 – Vertical Tutoring
2. Day 2 – Year 6s Starting in July
3. Day 3 – Down Time

Jennifer Stice (@mathchick5)

1. Day 1 – Activity Based Approach and the Success in “Doing Math“
2. Day 4 – Getting to Know You: Back to School Activities Using Technology

Kim Thomas Lee (@kimThomasLee)

1. Day 1 – Why I Love Teaching Fractions
2. Day 2 – I’m Still Thinking About Fractions
3. Day 3 – A Fraction of the Fractions Lessons, that I Still Love Teaching
4. Day 4 – Don’t Call me Average… That’s Mean, But at Least I Get to Eat the Smarties
5. Day 5 – Numeracy, do the Statistics Add Up? I Think They Are Scary
6. Day 6 – Numeracy Across the Curriculum, How do I Manage to Use Sport in my Lessons?
7. Day 7 – Why do we Need to be Numerate?
8. Day 8 -Numeracy Within MFL
9. Day 9 – Did I Use Numeracy Today? Of Course I Did, I Use It Everyday
10. Day 10 – Never Underestimate the Value of Tea
11. Day 11 – Design Technology:Numeracy in the Real World
12. Day 15 – A Quick Reference to Golf
13. Day 16 – Numeracy in English Lessons
14. Day 17 – Encouraging Literacy in Maths Lessons
15. Day 18 – Why Does a Maths Teacher Read the Core Texts?
16. Day 19 – Learning Styles, Starting With a Critique of My Learning Style
17. Day 20 – Seating Plans and Collaborative Learning Structures
18. Day 21 – Flipped Learning for Revision
19. Day 22 – Art and the Aesthetics of Mathematics
20. Day 23 – Starting Year 7, My Wishlist
21. Day 24 – Do Music and Maths Add Up
22. Day 25 – Students Say the Funniest Things
23. Day 26 – What About Those Who Don’t?
24. Day 27 – Will Your Job Use Maths? An Interesting Clip
25. Day 28 – Talk for Teaching
26. Day 29 – The Best Maths Quotes
27. Day 30 – The Pure Mathematical Beauty of Game Theory
28. Day 31 – The Maths and the Morals of BOGOF, BOGO and BOGOHP
29. Day 32 – The Economics, or is it Numeracy of Pocket Money
30. Day 33 – Numeracy Challenge Days
31. Day 34 – What About Those Times When Technology Fails
32. Day 35 – Rewards
33. Day 36 – If the World was a Village of a 100, One of my Favourite Resources
34. Day 37 – The New School Year, the Cost of Returning to School

@funASDteacher

1. Day 1 – I’m Here Because No-one Else Will Have Me
2. Day 2 – Match Your Books
3. Day 3 – Make Us Wait
4. Day 4 – Push Your Own Boundaries
5. Day 5 – Ode to the Envelope
6. Day 6 – Learn Like a Pirate
7. Day 7 – Where to Sit
8. Day 8 – Let’s Get Writing
9. Day 9 – M is for Autism
10. Day 10 – Notice the Small Things
11. Day 11 – Special Interests
12. Day 12 – Lose the Glare
13. Day 13 – Change the Objective
14. Day 14 – The Devil is in the Detail
15. Day 15 – Inclusion or Exclusion
16. Day 16 – The Obsession with Time
17. Day 17 – Braving The Technology
18. Day 18 – Rome Wasn’t Built in a Day
19. Day 19 – Support the Support Staff
20. Day 20 – Show Me How
21. Day 21 – If in Doubt, Make a List
22. Day 22 – Teaching Like a Pirate? Really?
23. Day 23 – Photocopier Traumas
24. Day 24 – Factor in the Anxiety
25. Day 25 – Routines: Friend or Foe?
26. Day 26 – Ask Questions
27. Day 27 – Making Mistakes
28. Day 28 – Time to Reboot
29. Day 29 – 5 Point Scale
30. Day 30 – The First Day
31. Day 31 – Group Work

It would be amazing to be able to add you to the above list……

Last week I made the (what I thought) throw-away comment that I was going to try and write a blog post every day of the holiday. I said this mainly because I want to try and get more regular in my posting, and this seems the perfect incentive! 

Christine (@MissNorledge) seemed keen to take part and has worked out that she has 51 posts to write!! This is a definite incentive for me to manage the whole summer as she has a much bigger summer of important events planned than I do!

A few others are joining in too, please feel free to join in!

Tomorrow afternoon I will create a post where I will continually link to all the posts everyone writes, so please remember to tweet your posts with the hashtag #summerblogchallenge so that me and Christine can link them 😉

I break up tomorrow so I will be officially starting my challenge on Friday…….