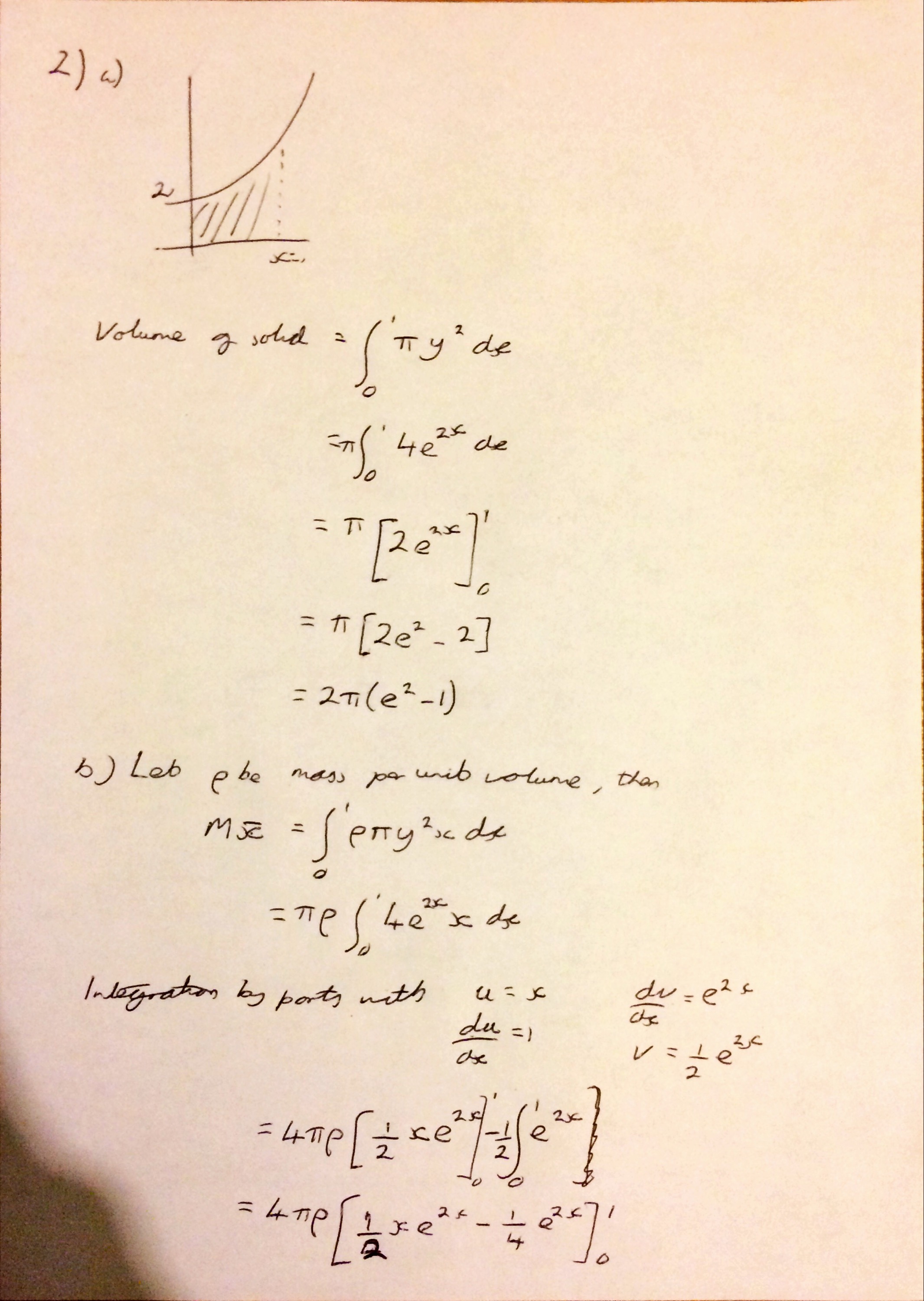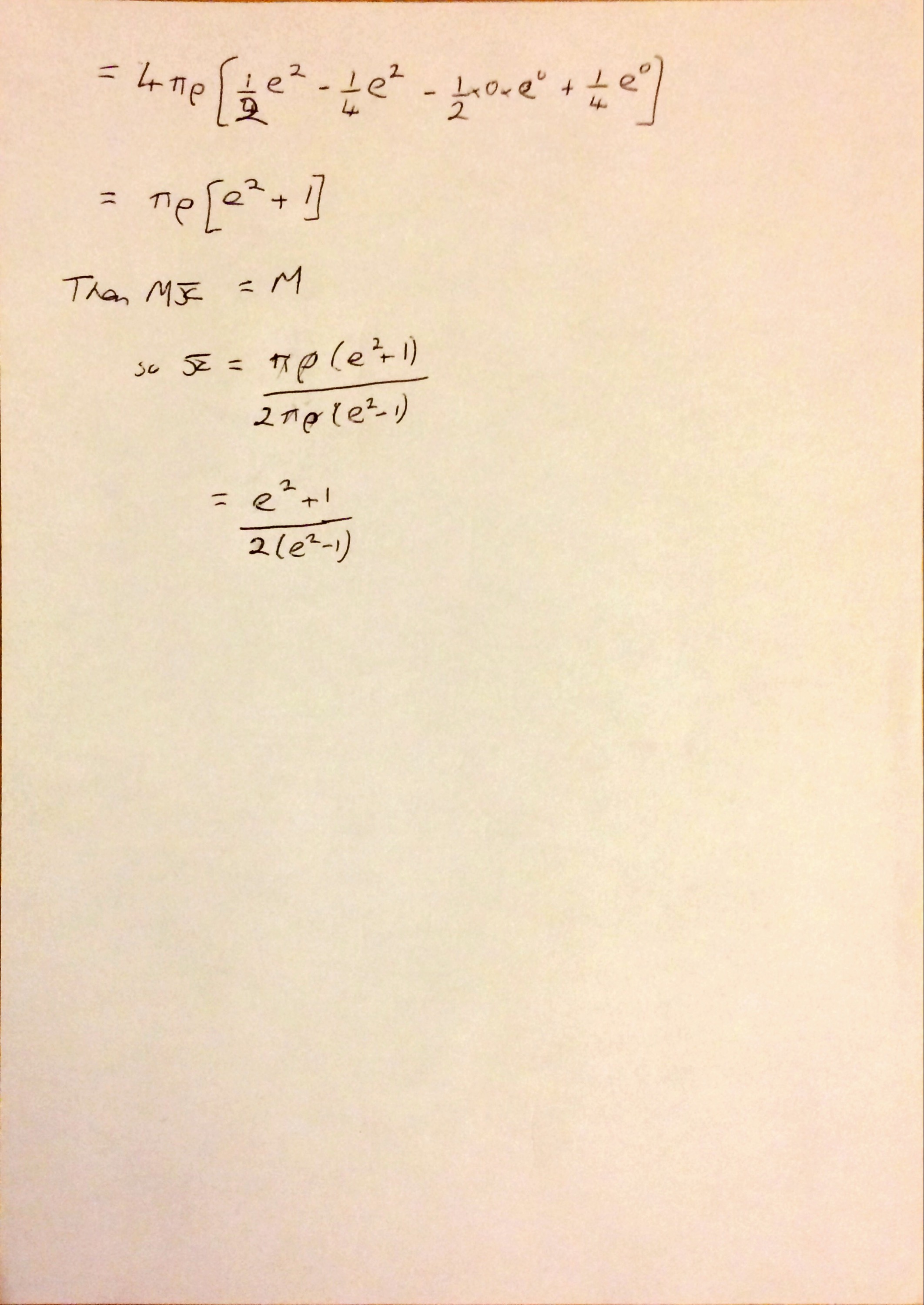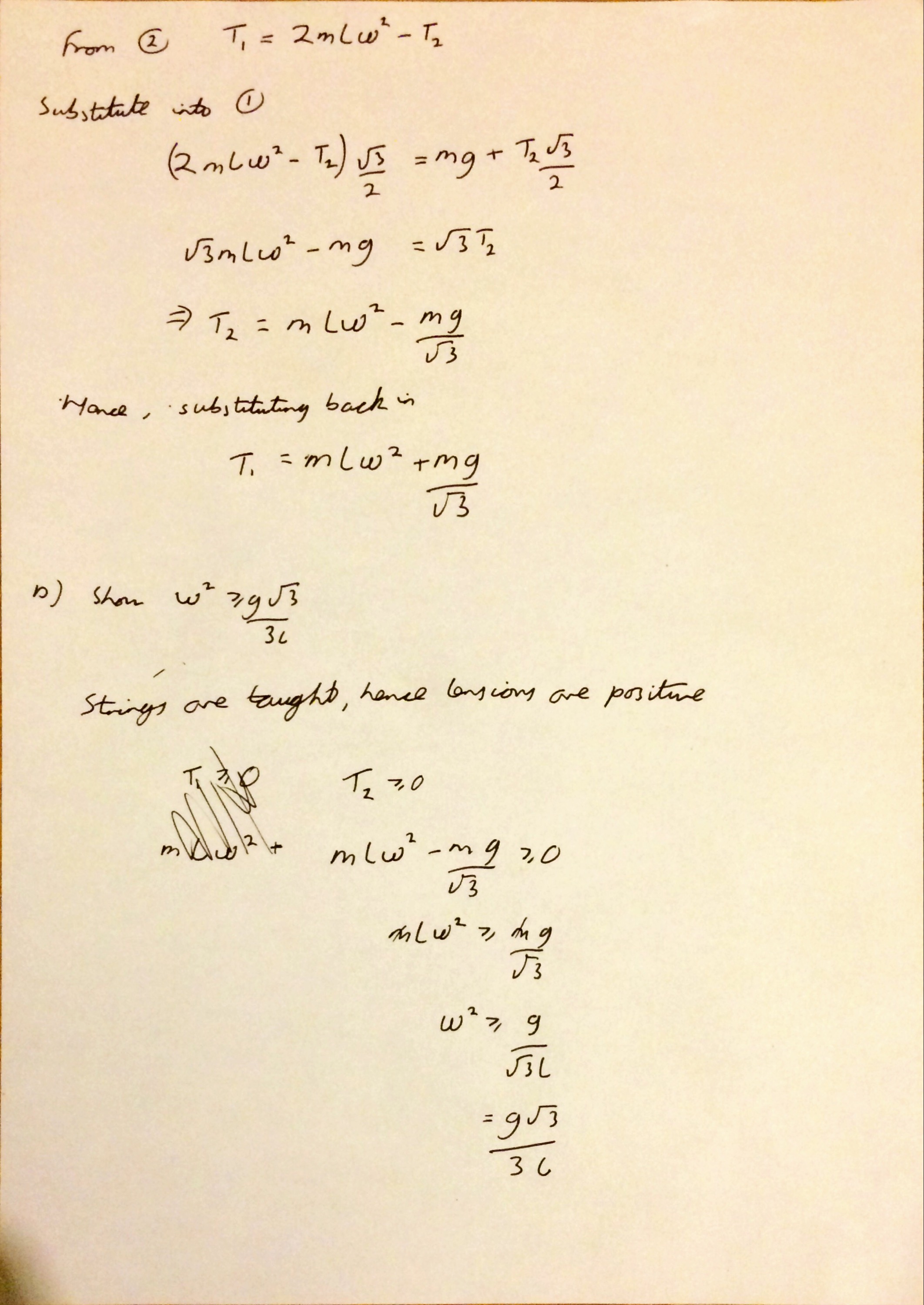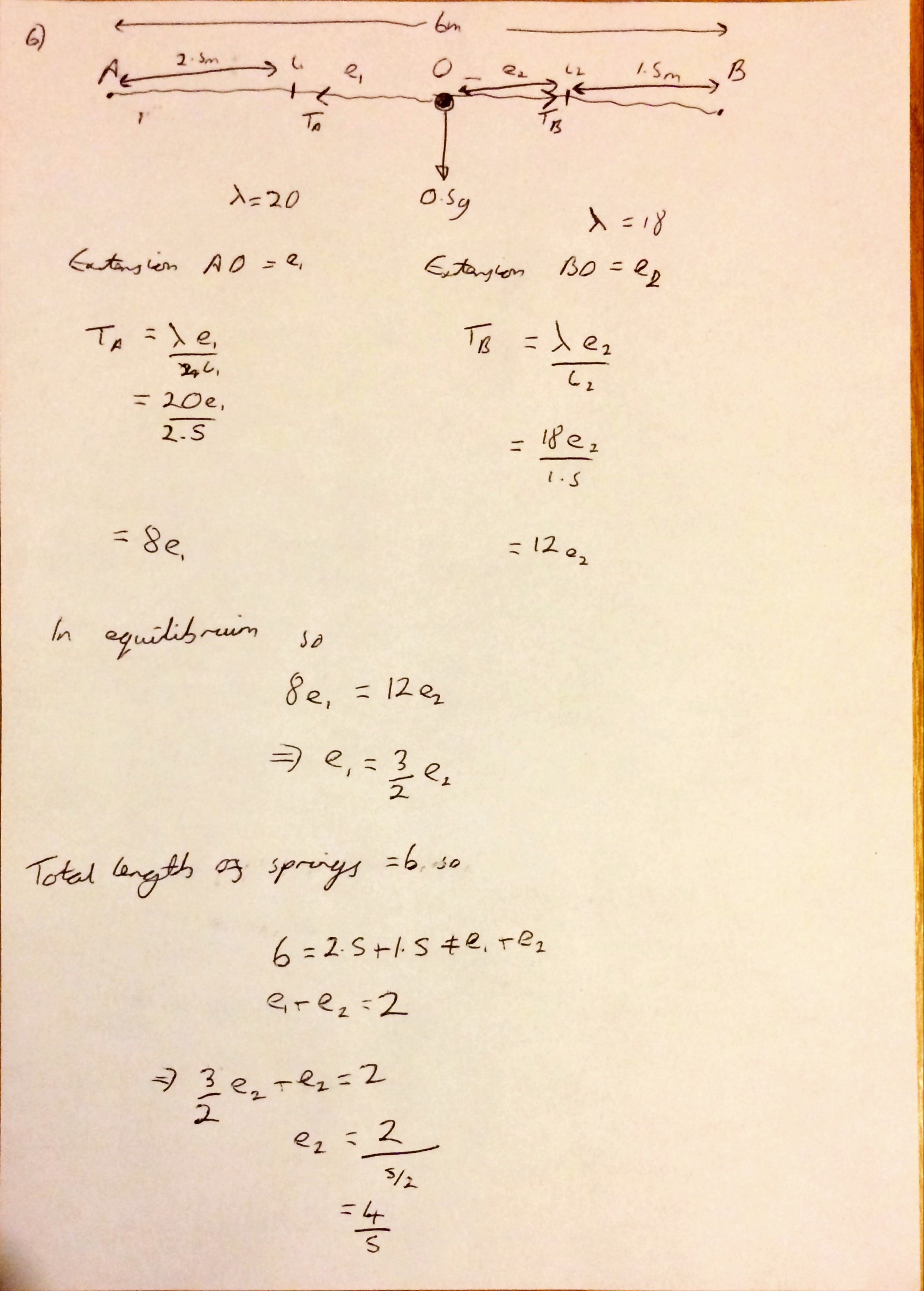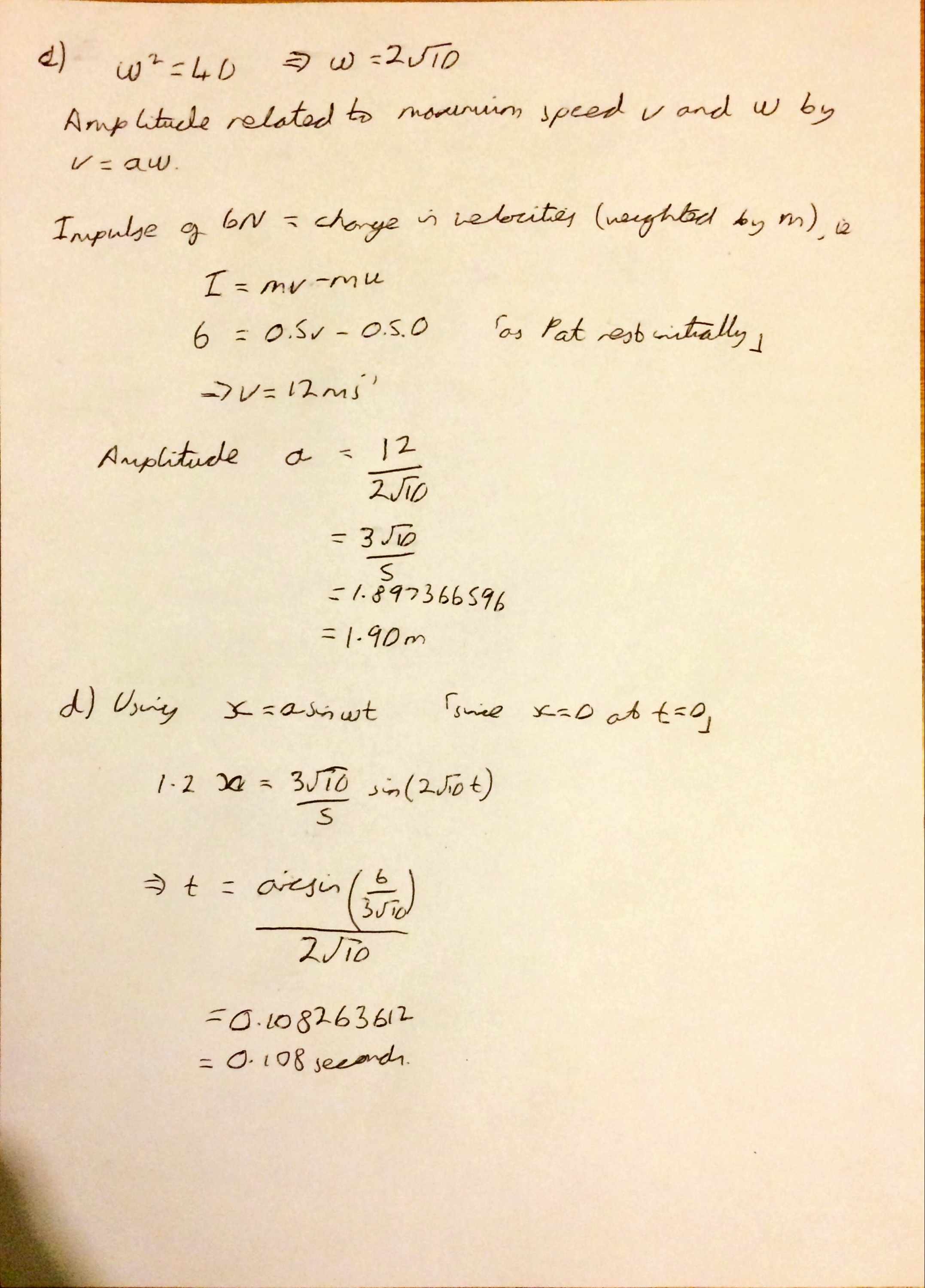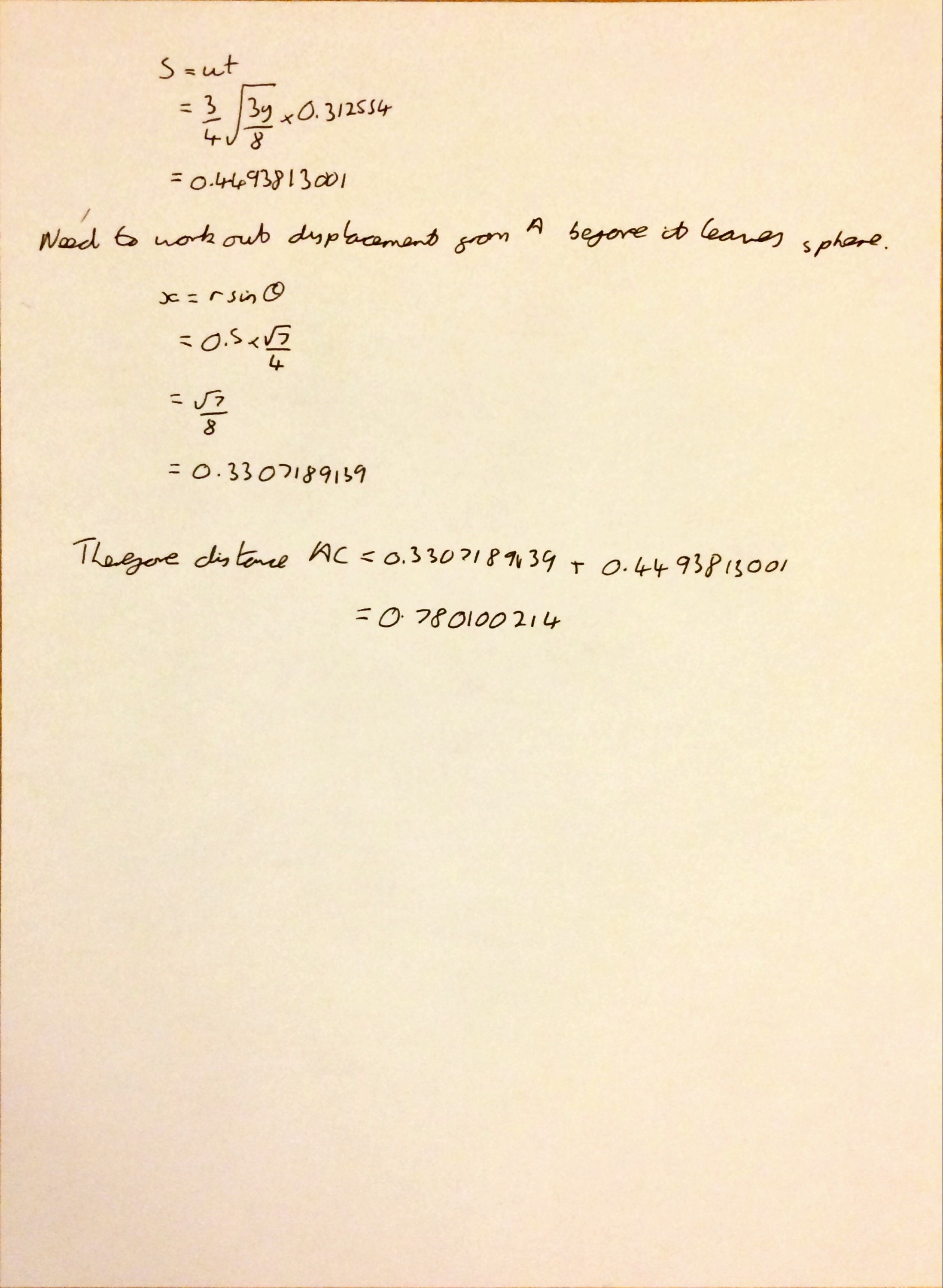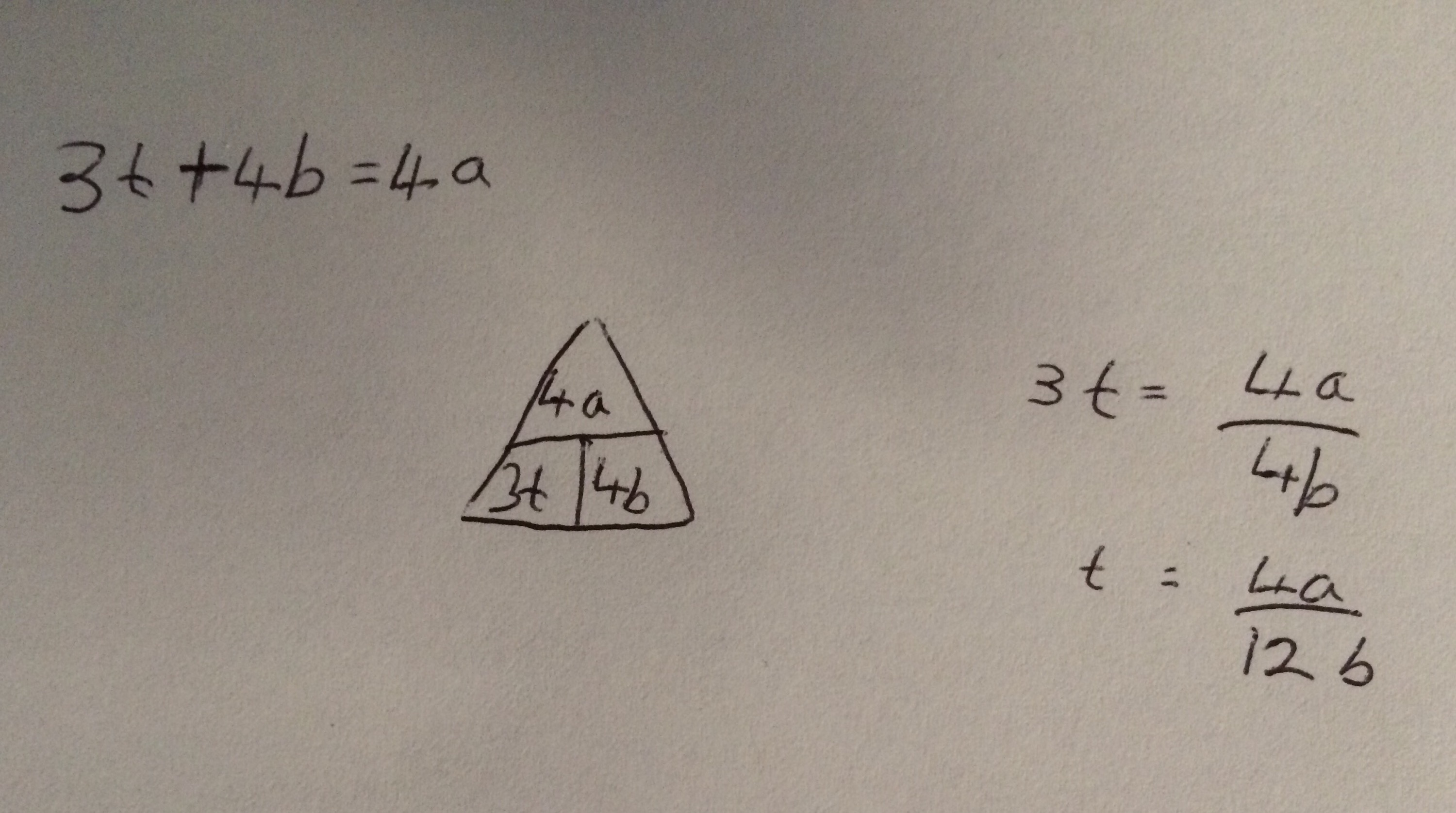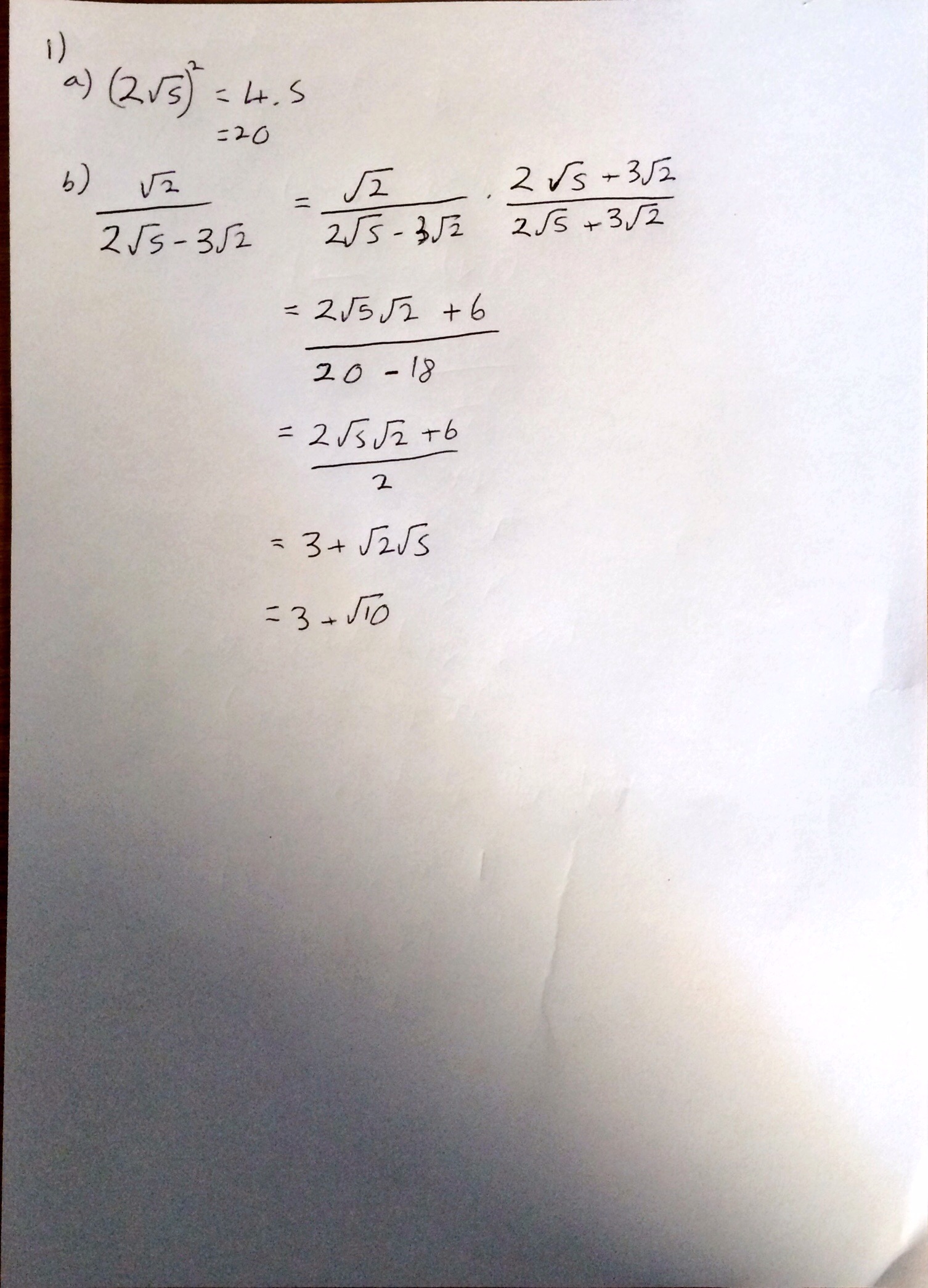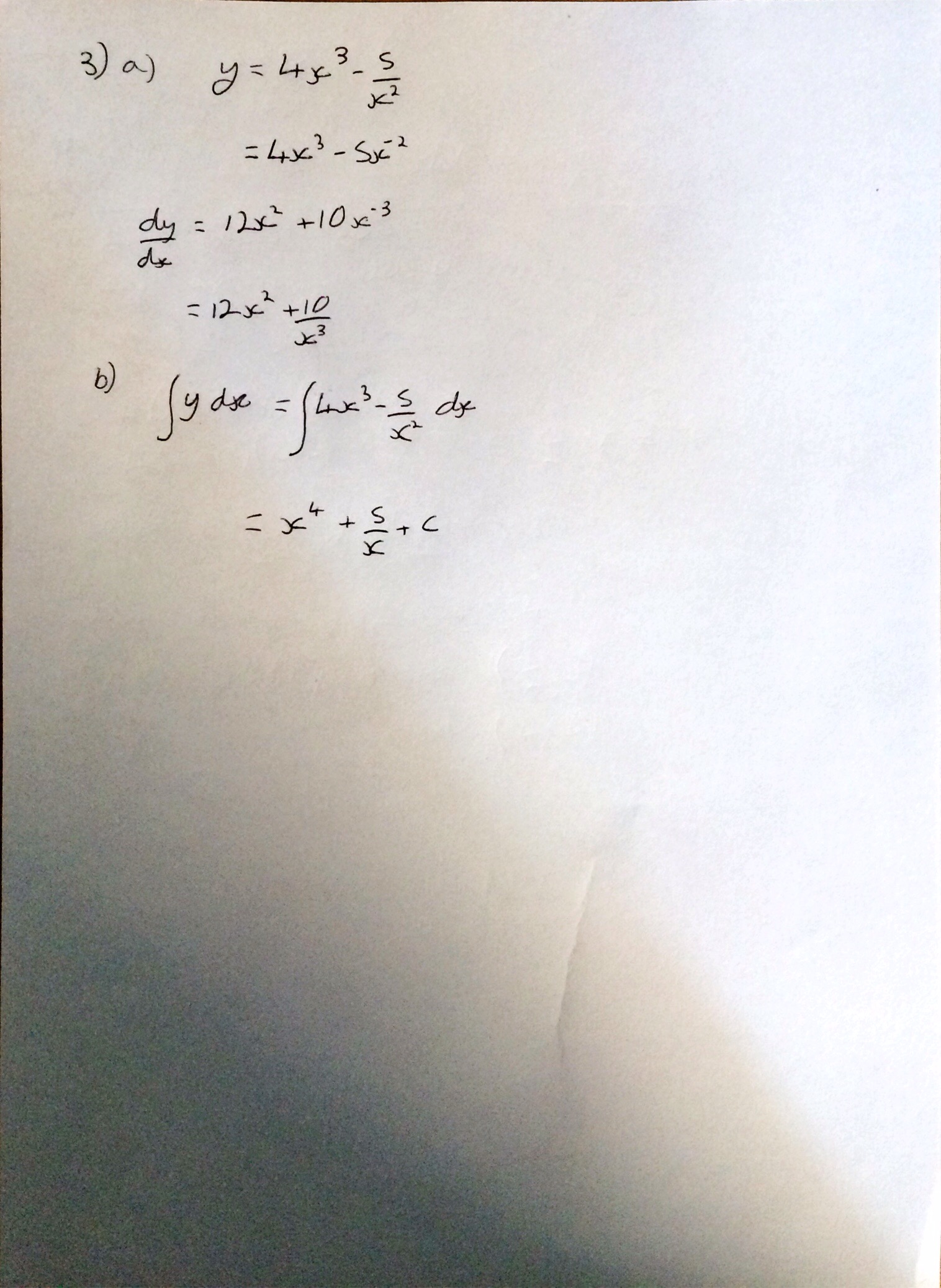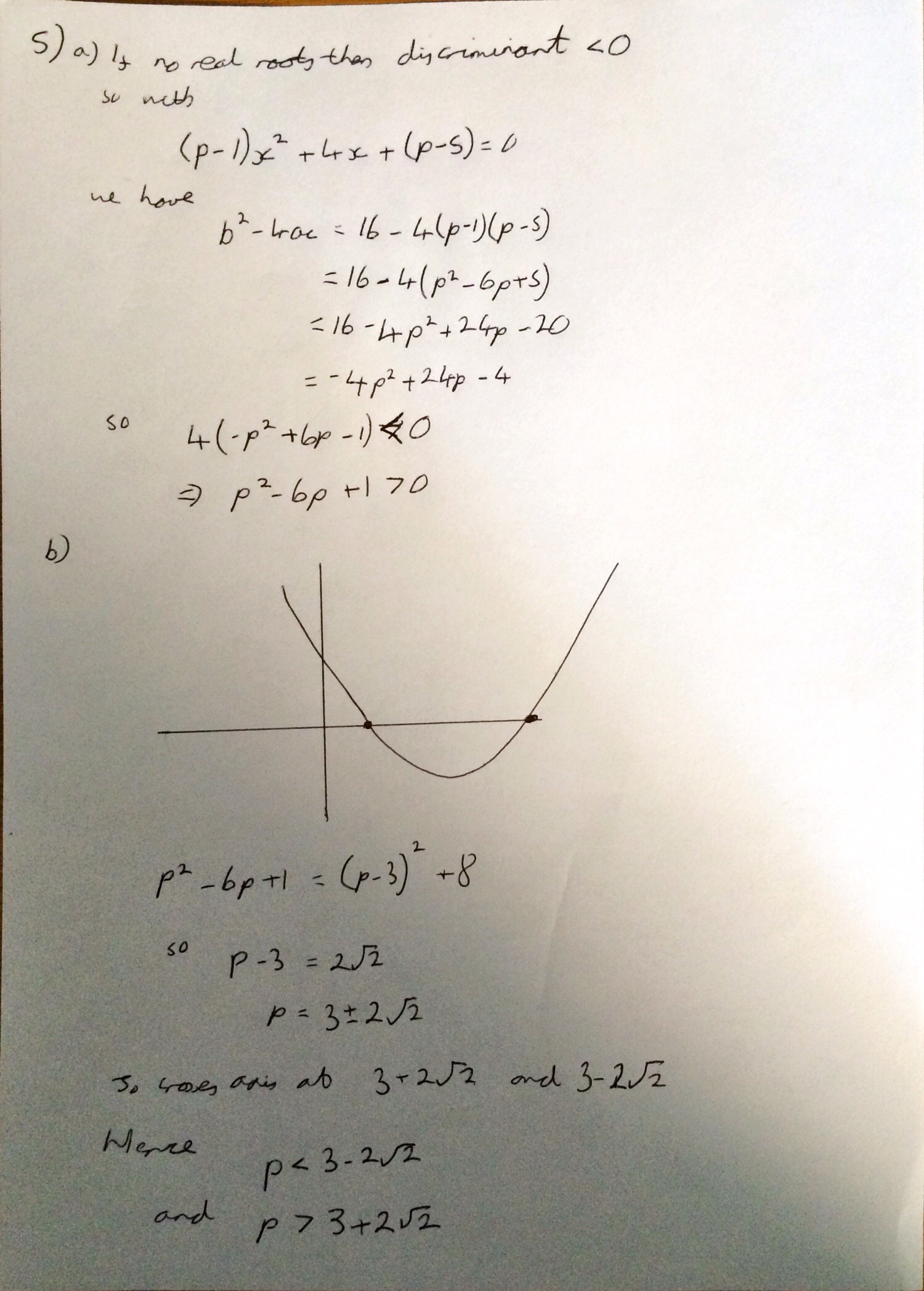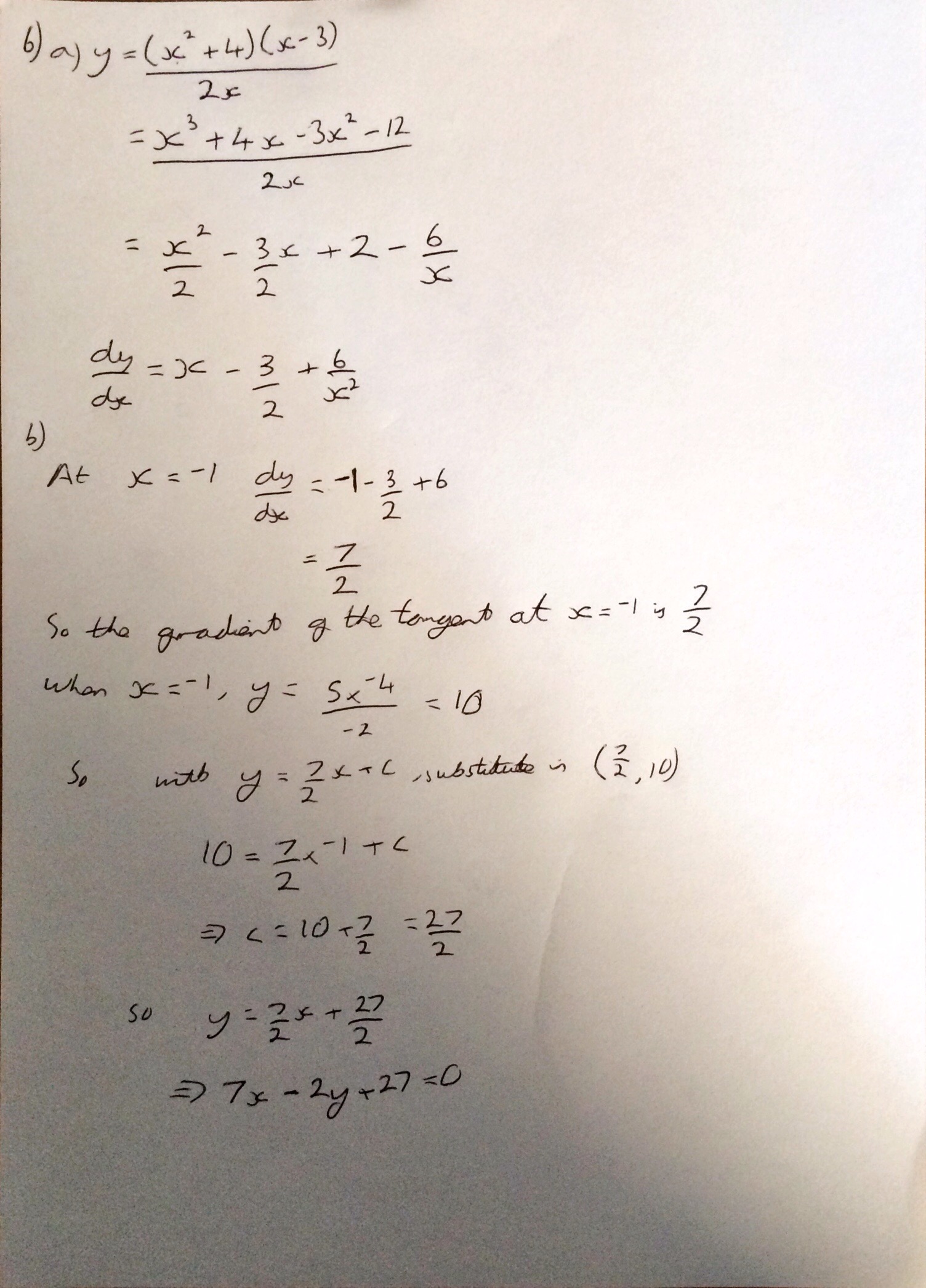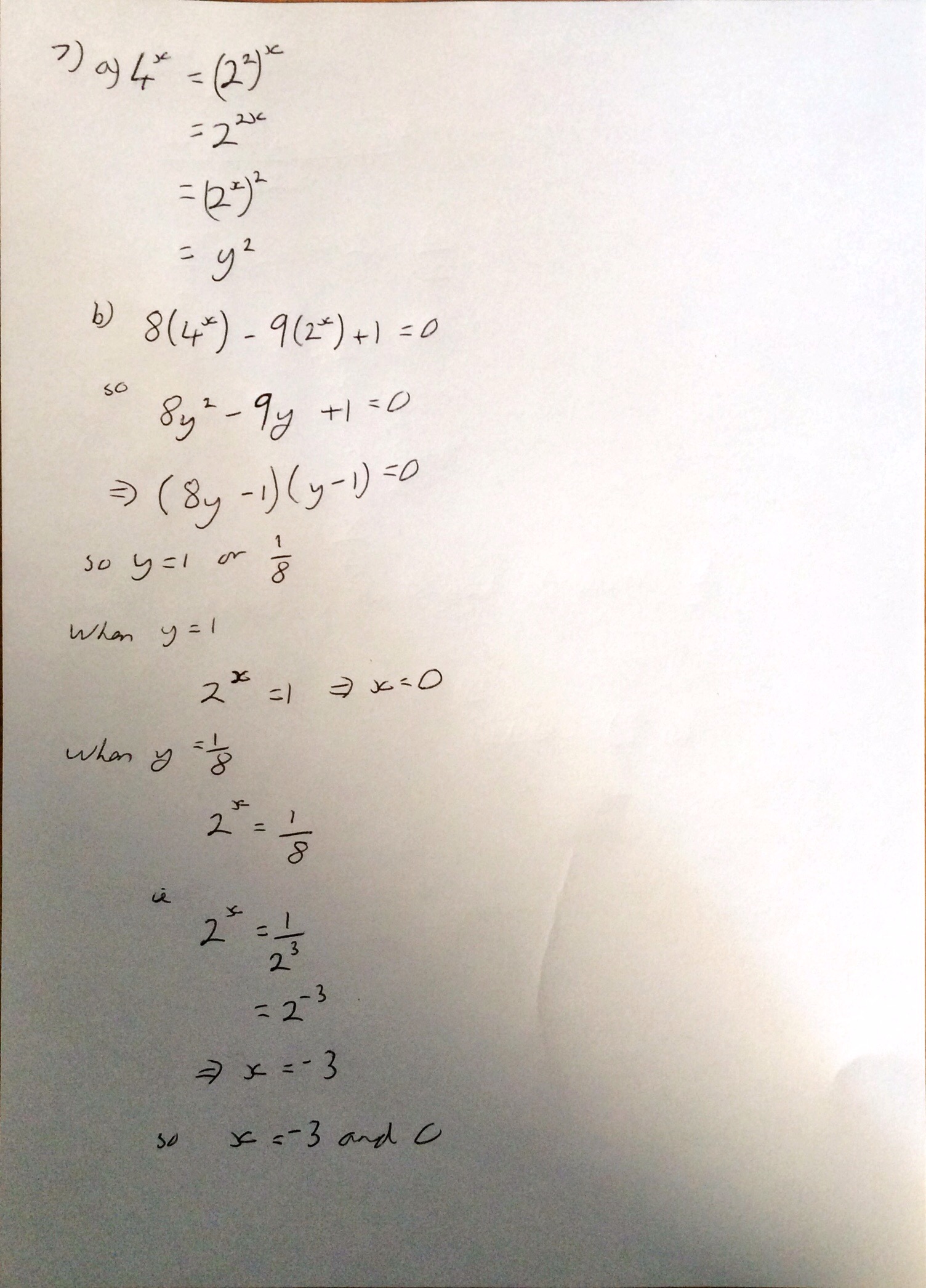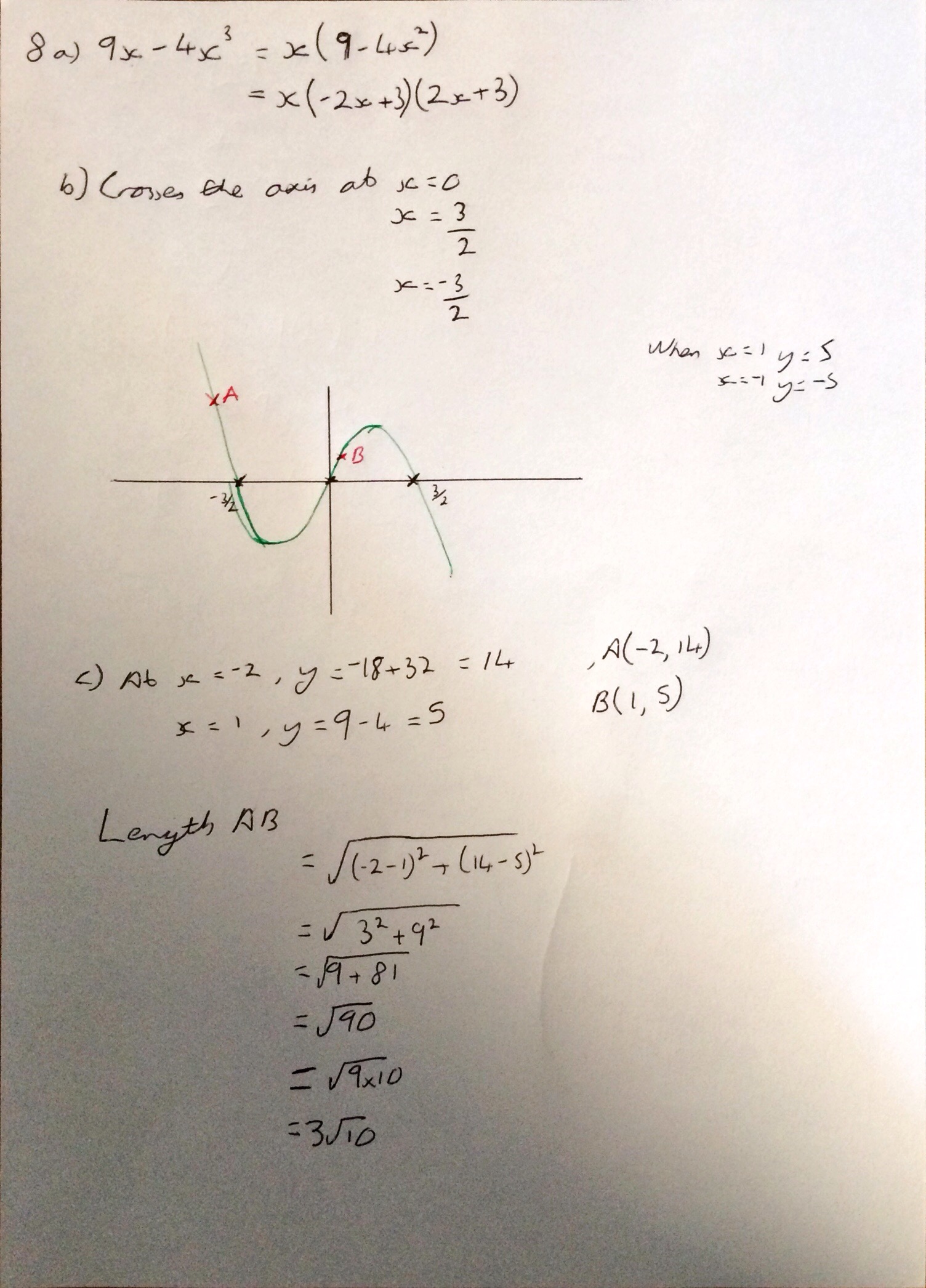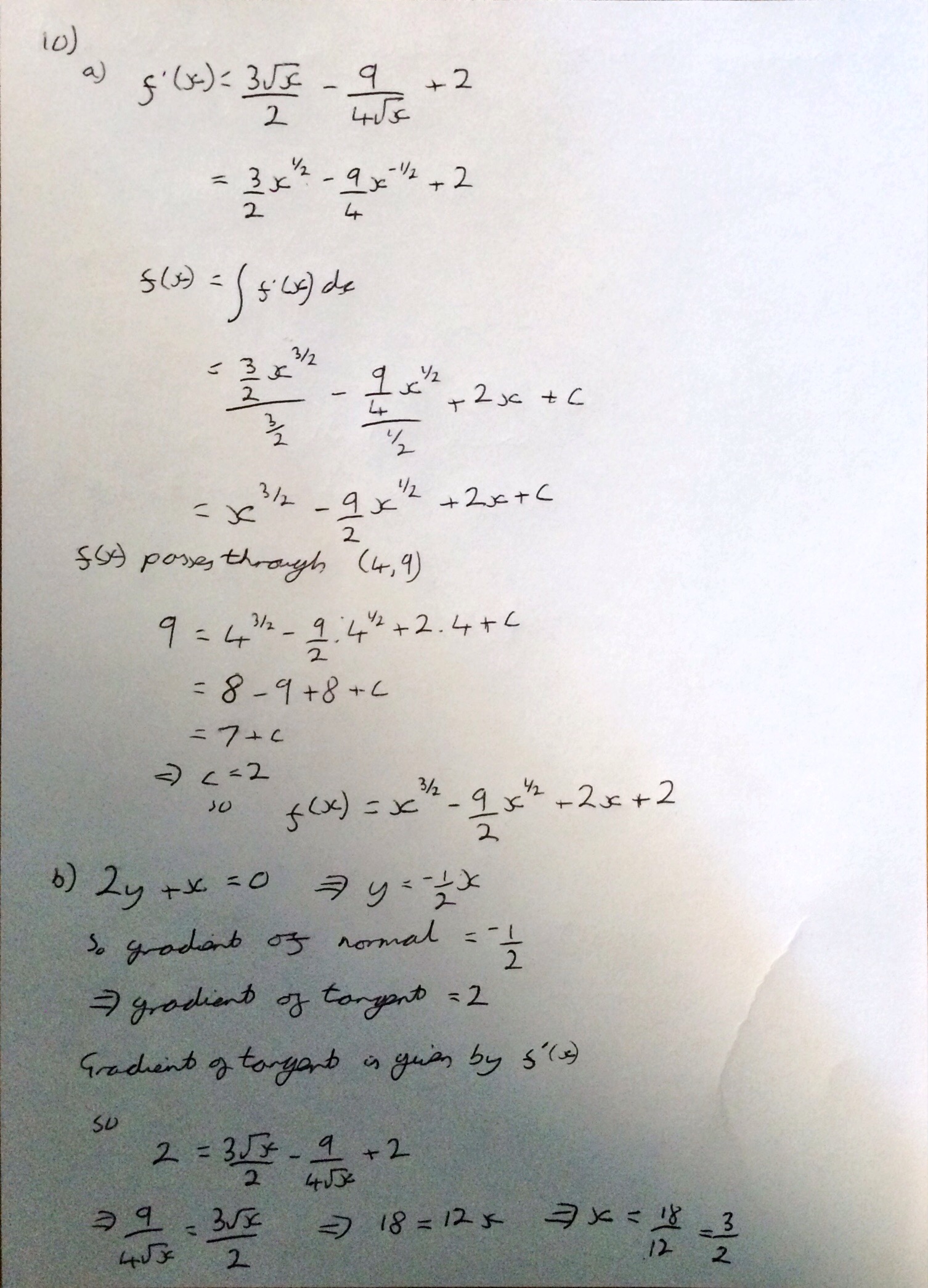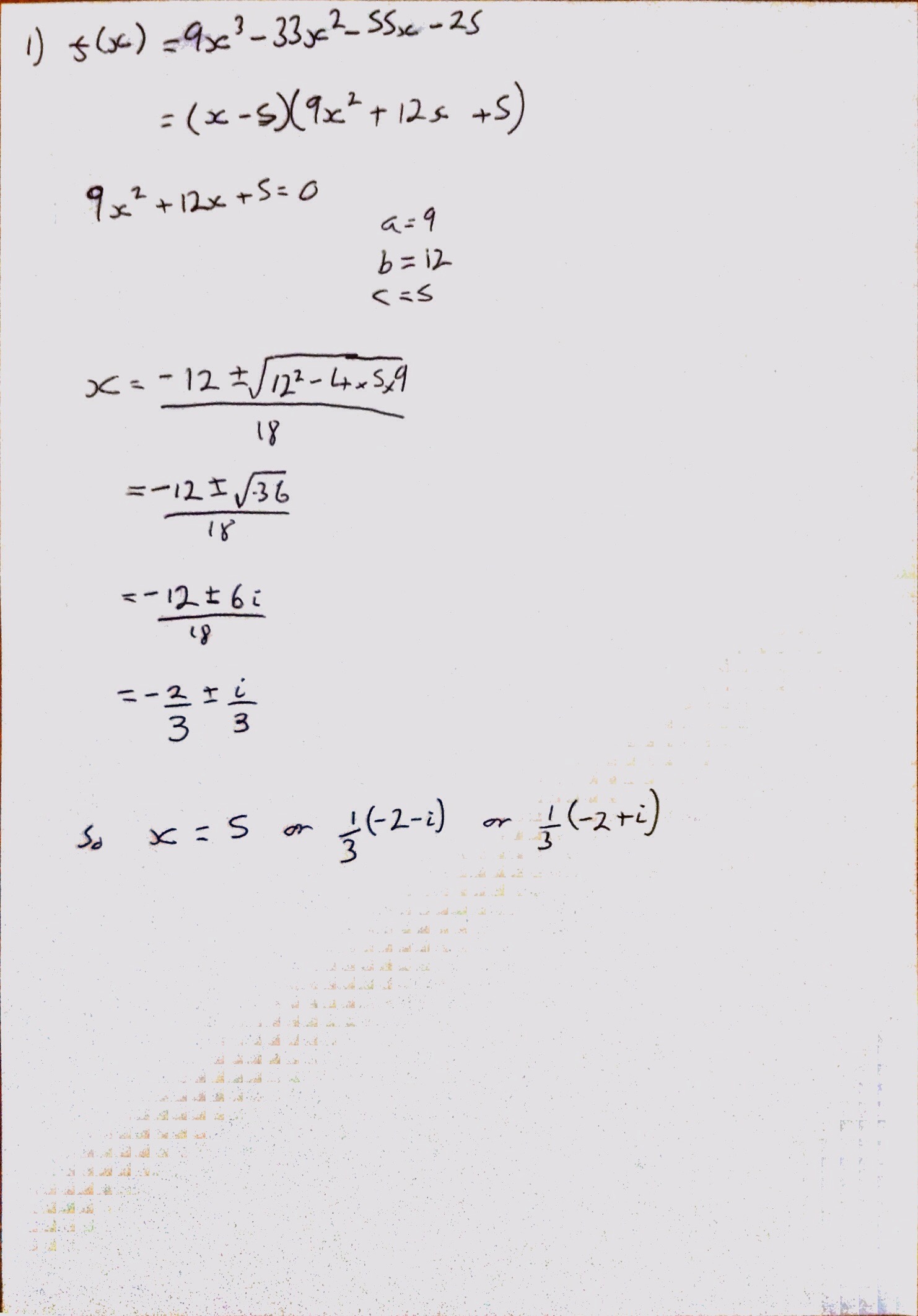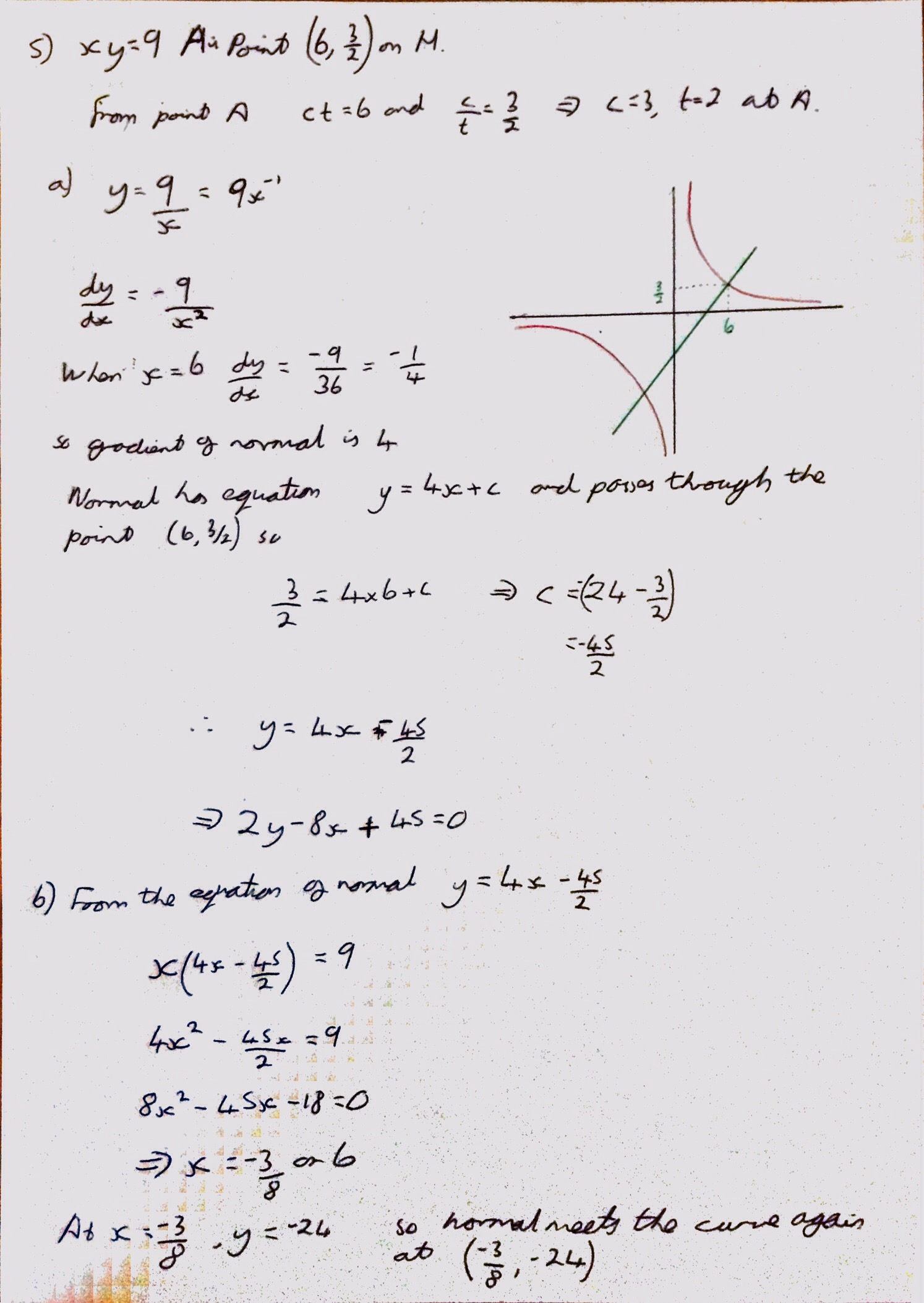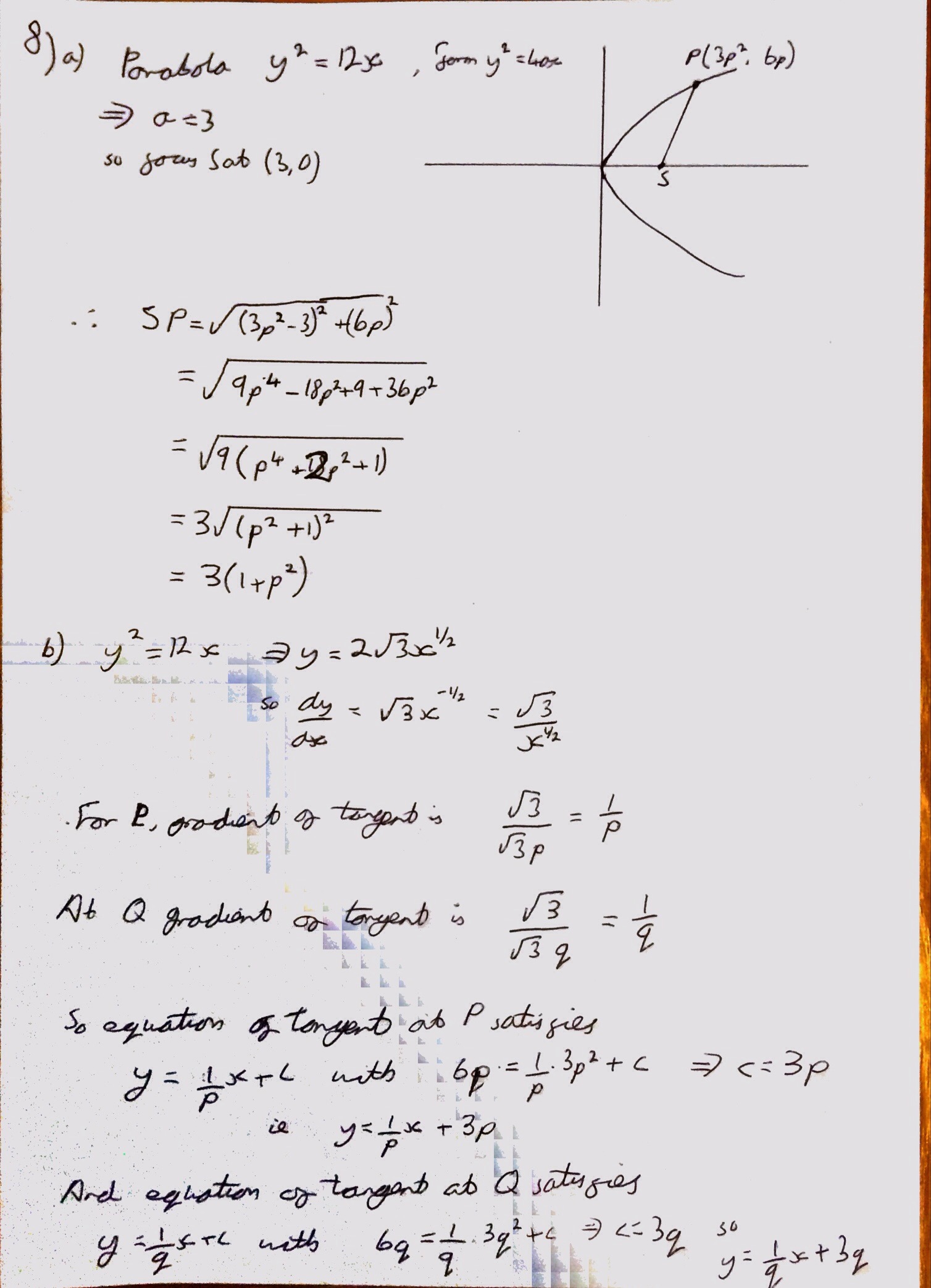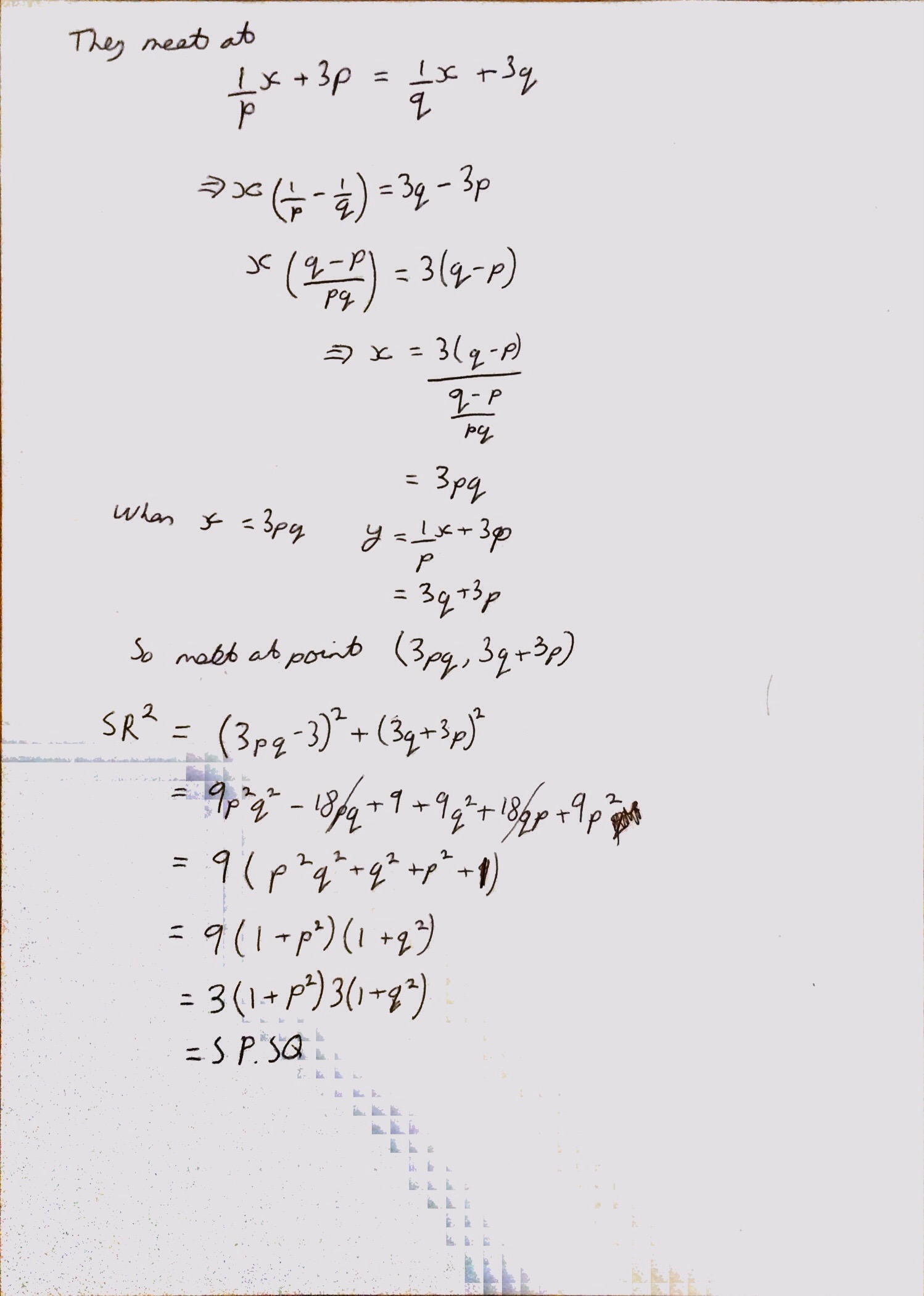Month: May 2015

Next year I am likely to be teaching Mechanics 3 to my further mathematicians and so I thought I should have a go at this years exam paper (1 person sat it at school so I had a copy of it). After seeing this video I was a little nervous as I hadn’t looked at this since I did my A Levels, however I didn’t find it too bad with a bit of help from my old A Level textbook:

   
Question 1 I thought was pretty straightforward – once I had refreshed my memory of how to calculate elastic potential energy it was just an energy conservation question. Please excuse that I have written Hooke without a capital letter.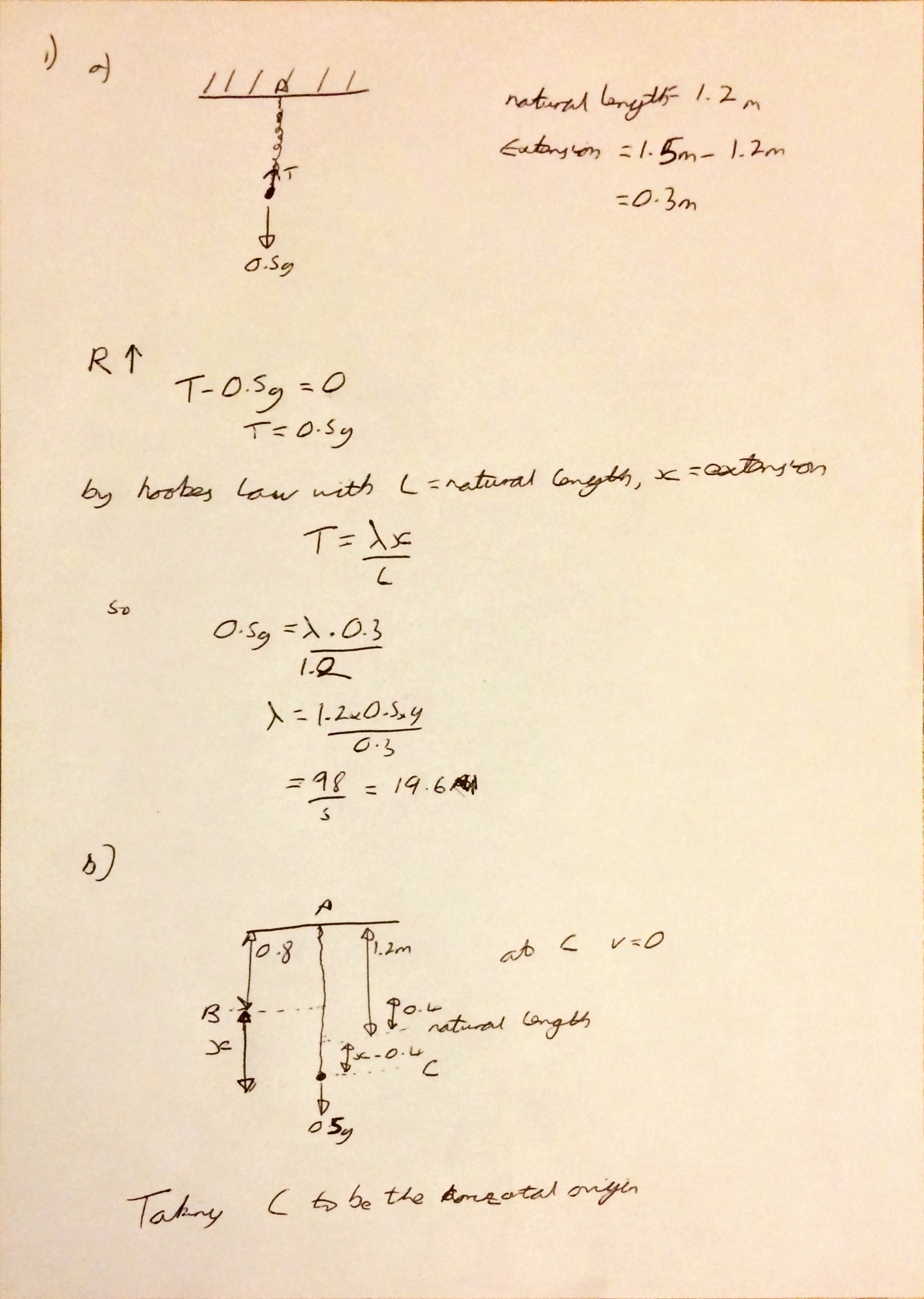

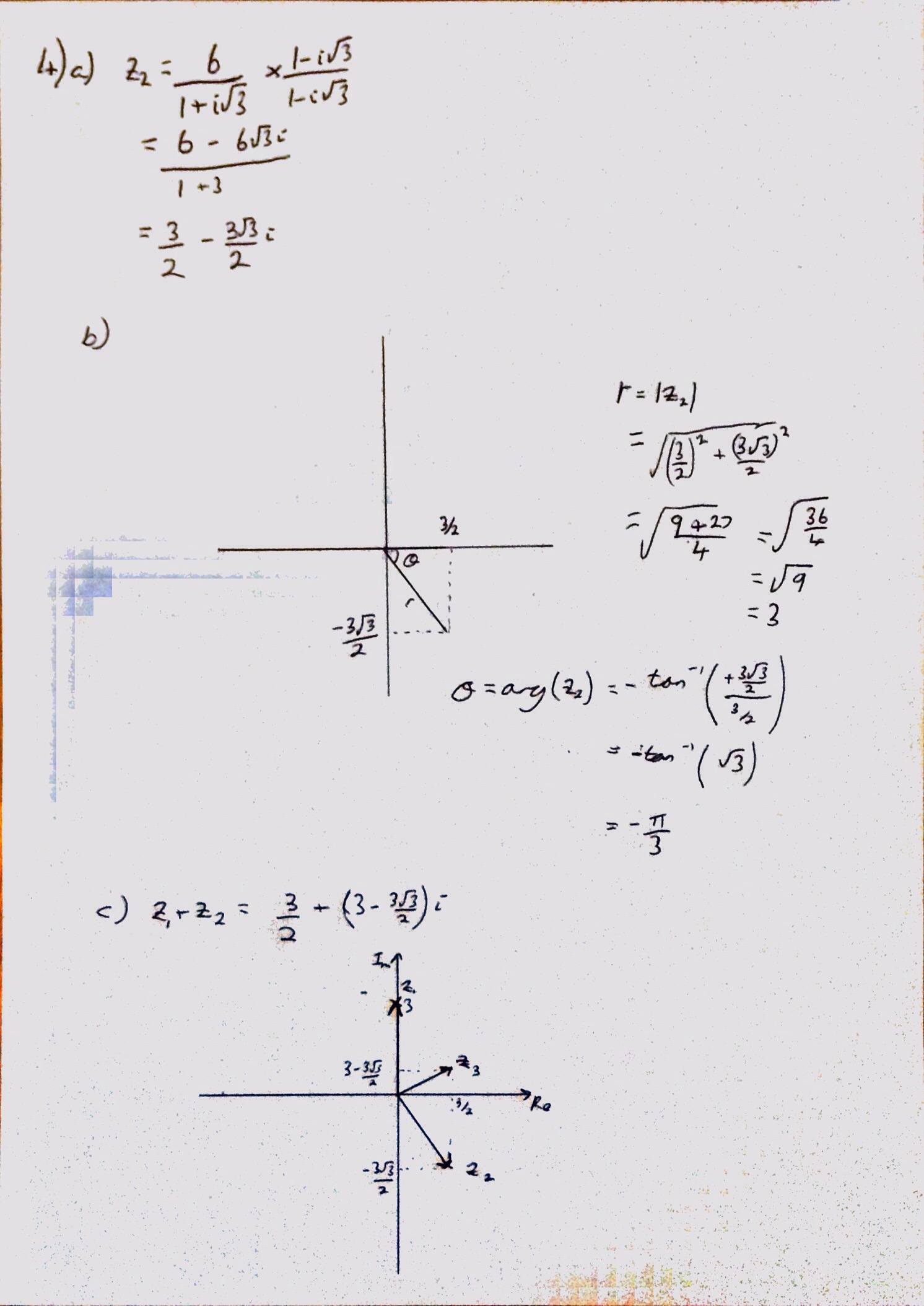
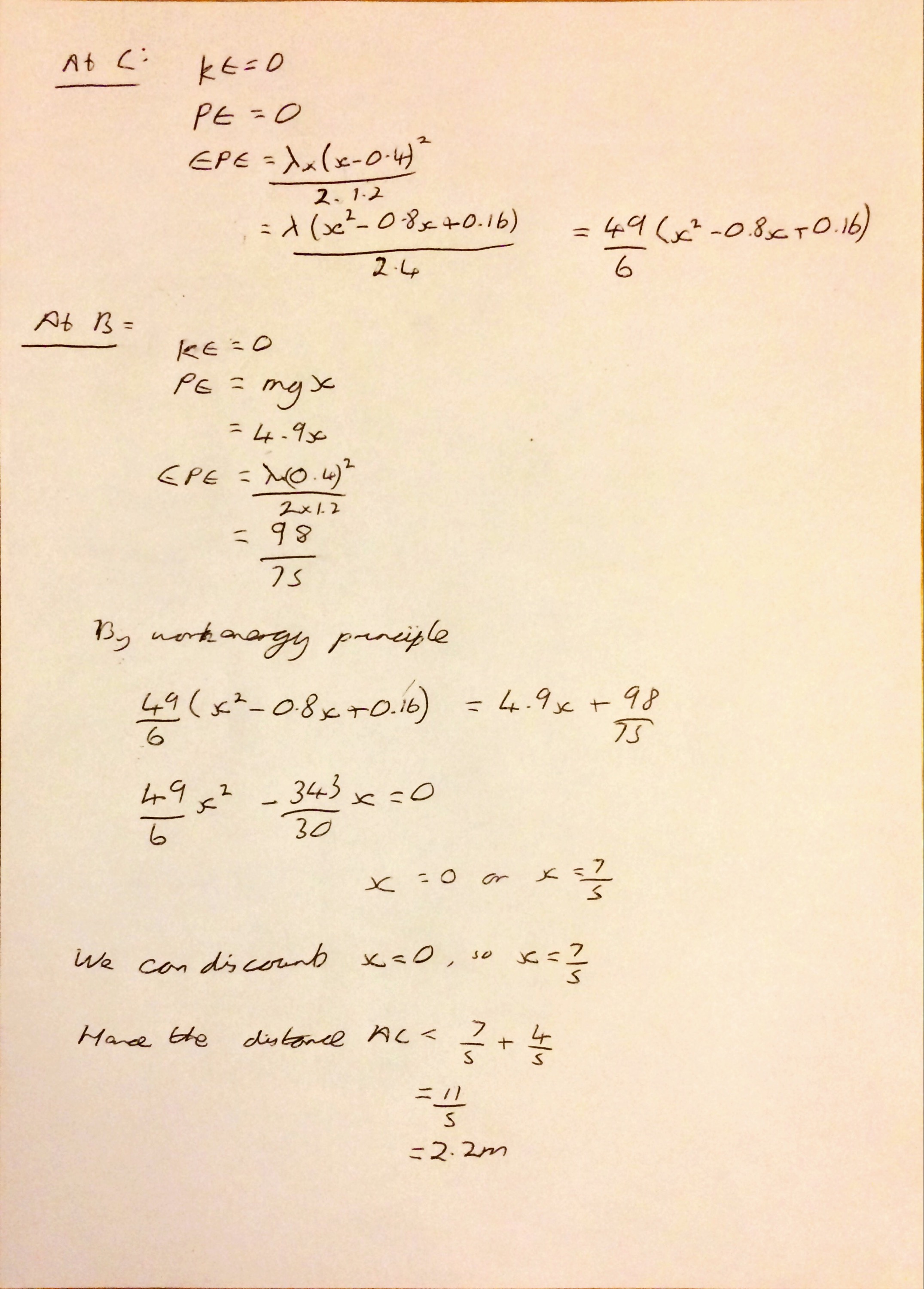Question 2 was nice, as long as you could remember how to find volumes of revolution, and then use this to find \(\bar{x}\)

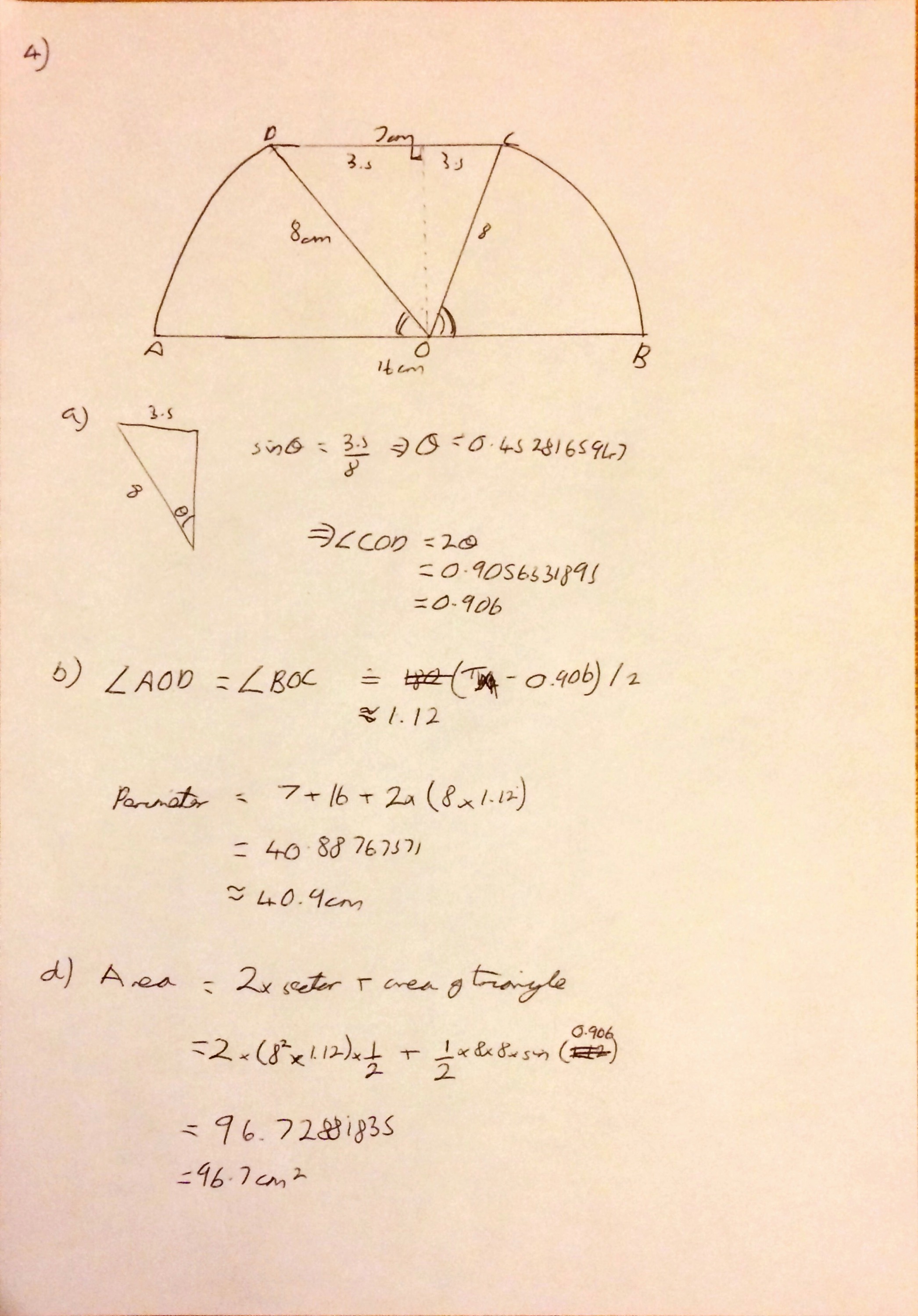
For Question 3 I realised that sometimes I have no intuition with the mechanics questions. Even though it was asking you to find the tensions in each string I still expected them to come out equally – of course in hindsight this clearly wouldn’t have made much sense. The circular motion stuff came back to me quicker than I expected to be honest, and this question dropped out quite nicely. 

Question 4 was a nice power type question, I thought it was very like an M2 question, just with the complication of non constant acceleration. I really like how the question required you to use the Trapezium rule. As a numerics guy I think how the numerical methods are presented at A Level is incredibly sad. The trapezium rule is great, and it could be used so much in the applied modules – students wouldn’t like being asked to use something from Core 2 in other modules though. I think I may have to write about the Trapezium rule……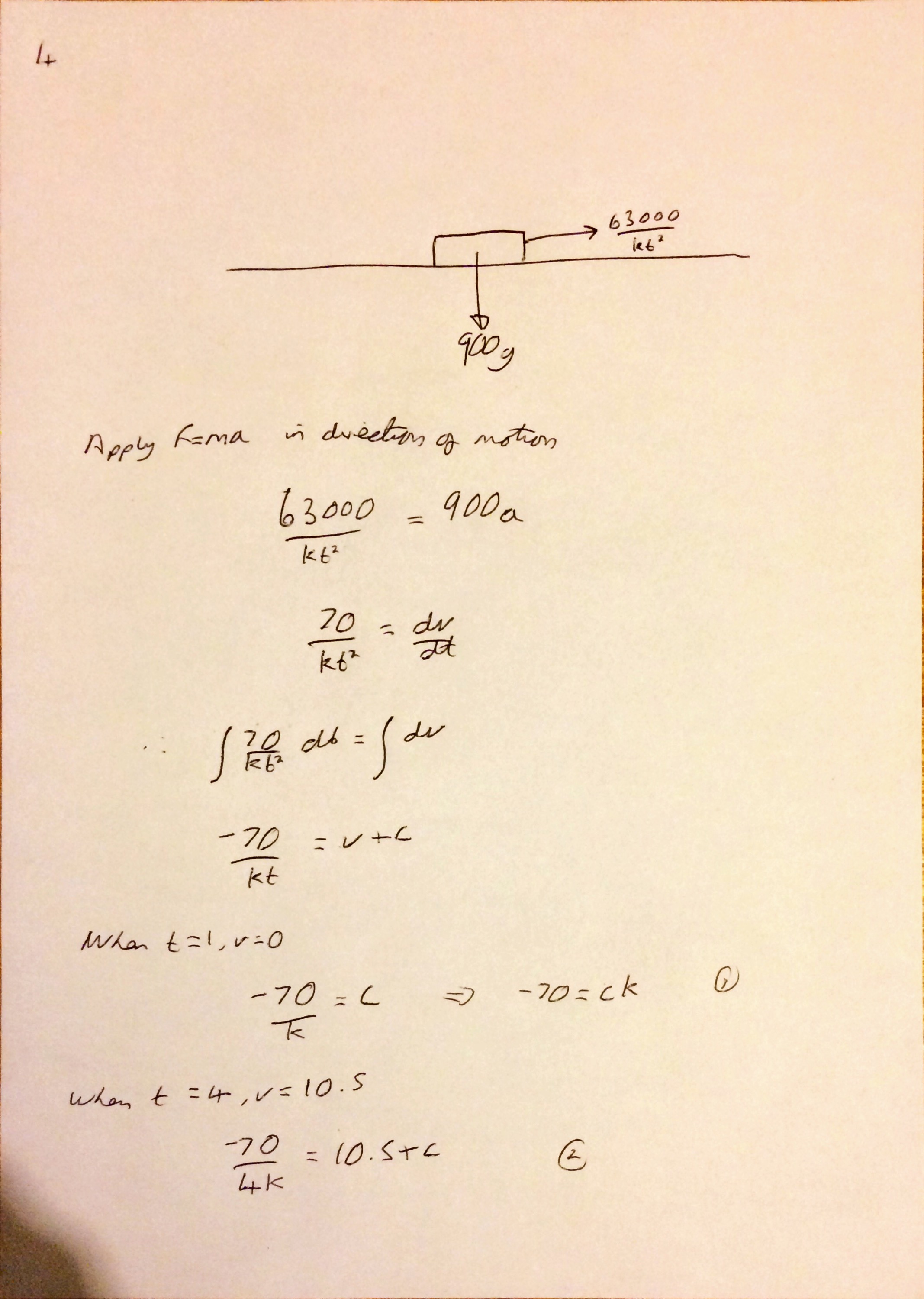   

Question 5 is a nice centres of mass of a 3D solid. It considers a spindle formed of two cones. In hindsight it would have made more sense for me to work out the Center of mass using moments from A instead of taking moments from B

I can remember loving questions like Question 6 when I did A level, and I still quite enjoy showing that a particle connected to two springs exhibits simple harmonic motion. Like many questions as long as you are comfortable with applying F=ma and solving simultaneous equations it is fairly straight forward. 

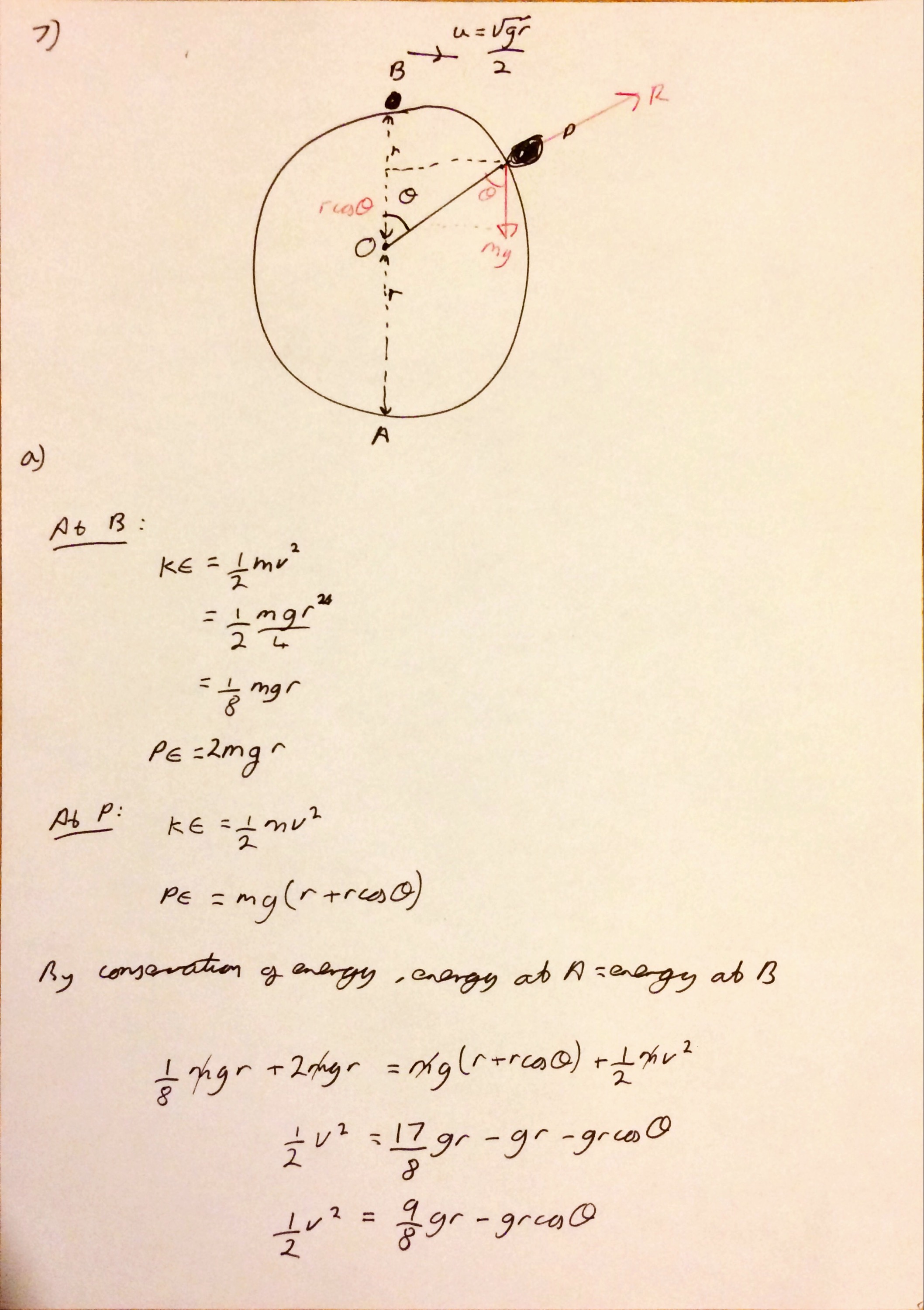
The final question considers a particle moving on the surface of a sphere and uses conservation of energy and F=ma. I wouldn’t be surprised if some students forgot to add the horizontal distance moved whilst on the sphere in the final part.   

Formula triangles are quite prevalent in the UK (I’m not about elsewhere to be honest) – especially in science lessons and when right angled triangle trigonometry is taught. A typical example is the following for the relationship between speed, distance and time:

  
I’ve expressed my dislike (hatred is perhaps too strong a word) of formula triangles on Twitter before and others have written about them including Stephen Cavadino. Like Stephen my main reason for not being a fan of them is that they are usually introduced as a “trick” for use in particular situations with no reference to the underlying mathematics. 

One of my students when looking at rearranging formulae was asked to make t the subject of an equation and drew a formula triangle as shown below (I’ve re-written it!)  

When I asked why they had drawn a formula triangle they responded “well there are 3 terms so it’s a formula triangle question”. I’ve never seen this misconception before, I guess it is maybe down to formula triangles being used only for 3 term formulae and then this link becoming solidified in the student. 

When I probed a bit further and asked things like “why have you picked 4a to be on the top” after a while they realised their mistake. I can’t help thinking that this wouldn’t have come about if they had never seen a formula triangle and instead had just had plenty of opportunity to practice rearranging formulae. 

Yesterday I went to an Intermediate Geogebra course at the Geogebra Institute of Sheffield run by Mark Dabbs. It  was really good, and I have picked up lots of things I hadn’t realised (but probably should have done). For example, the fact that the input bar can be moved to the top of the screen so that students can more easily see it when projected onto a screen. Or that it is possible to adjust properties of many objects by just highlighting them.

I have lots of ideas of Geogebra things to do, which I’m sure I will post on here as I do them, but I thought I’d quickly share a trick (I’m sure some of you already do this) that gets rid of a little niggle of mine.

When teaching circle theorems I think it is nice to let them have a bit of time to discover them for themselves. With Geogebra you can easily create dynamic worksheets for them to explore. I’ve had a few sheets like the one below for demonstrating the “angle subtended at the centre” theorem

The angle at the centre is obviously meant to be twice the angle at the circumference but \( 2 \times 47.66 = 95.32 \) which is not \(95.31 \). Of course this is just an artefact of the rounding done to represent the angle to two decimal places, but it does distract from what I am hoping the students will spot. This could prompt a nice discussion about rounding errors and limits of accuracy, and of course could be mitigated somewhat by disiplaying more decimal places. But, I had always thought it would be nice if I could restrict the angle at the centre to prevent this from happening – which it turns out is easy to do. Using GeoGebra’s Sequence command (which behaves much like a for loop in a conventional programming language), we can generate a set of points around the circle such that the angle at the centre is either a whole number or a multiple of a half. This means that the angle at the edge will always be exactly represented in the two decimal places restriction.

Once the circle with centre A has been created (by default it is given the name c), I placed one point on the circumference, call it A’ say with the command
[code] A + (Radius[ c],0] [/code]. I then rotated this single point around the circle in increments of  0.5 degrees using the command [code] Sequence[Rotate[A’,kº,A],k,1,360,0.5] [/code]. This rotates the point A’ about the centre of the circle by k degrees in increments of 0.5 degrees, creating a list of points, which by default is named list1. Then  you need to hide the points around the circle from the graphics view, before creating three points B,C and D on the circumference. Once you have added in the appropriate line segments the angle can be added in using the angl tool. The final step is to redefine the definition of the points B, C and D from [code] Point[ c] [/code] to [code] Point[list1] [/code] as shown below in the screen shot from the iPad app – it is much easier to do this in the desktop version.

I have hosted both versions of these basic applets on my website here.

I really would recommnd that anyone who likes using GeoGebra to attend one of Mrk’s courses, it was a great way to spend a few hours and I am hoping to go to the advanced course in July.

Many people came out of this exam saying it was hard, even some of my FM class said they didn’t particularly enjoy it. Compared to the 2014  paper i do think it was a bit harder; the lack of a question concerning the trapezium rule was a noticeable omission of some easy marks. 

Starting on a question by question basis, Question 1 was a straightforward application of the binomial expansion, only requiring 3 terms to be given. This is esppecially easy as you are given the binomial expansion in the formula book! I think this was a very nice start ot the paper and hopefully would have boosted the confidence of the students sitting the paper.

  
Moving on to question 2 we had, what I think, is quite a nice circle geometry question. Finding the equation of the circle is straightforward, given that you are told the centre and a point on the circle  – conceptually I think this is easier the starting part of the equivalent question last year. We then go on to find the equation of a tangent to the circle requiring a bit of memory of circle theorems from GCSE and the properties of perpendicular lines.

Some students that I have spoken to have said that they found Question 3 hard, it is definitely more challenging than the equivalent 2014 question, however it is almost identical to the corresponding question in the 2013 paper. Just use the remainder theorem and factor theorem to form two equations in terms of \(a\) and \(b\) and then solve. It factorises nicely, into the factor given and a differenc of two squares (as long as you recognise that a factor of 3 can be pulled out).

  
The area and perimeter of sectors question (Question 4) seems fairly typical to me, I think some may have found the first part of the question a bit tricky, and won’t have thought to break the triangle into two right angled triangles and then double it. Once the angles have been calculated, completing the rest of the calculation is fairly simple. I guess some may have forgotten to add the base length in when calculating the perimeter. Please marvel at my awful diagram for this question, and note I used the incorrect angle for the last part at first!

  
Question 5 concerned geometric series and to me feels harder than the equivalent question last year. However, as the formulae are all given in the formula book, forming the equations (simultaneous equations again!) required for the first part shouldn’t be too difficult, and solving them drops out nicely.  The second part of this qquestion requires a bit more thought and the use of logarithms to efficiently solve  – I also think a few people will have forgotten to round up to the nearest integer.

   
  
Question 6 moved on to integration and finding the area under a curve. They even gave you the points where the curve crossed the axis and a very helpful picture  of the shaded region to find the area. The tricky part I imagine would be remembering to take the absolute value of the area of the first region when working out the total area.

  
Question 7 was the main logarithm question and I think this was slightly easier than the last two years as it was obviously a logarithm question and no curve sketching was required. As long as students are systematic in their application of the logarithm rules part b should be ok, though there are plenty of places for arithmetic errors to creep in.

 
I think the trigonometry question will have thrown a few people: you don’t often see \(3\theta\) in a question, but apart from that part a is ok as long as they remember the period of \(\tan (3\theta) \)  is a third of that of the period of \(\tan ( \theta) \). The phrasing of part b seems to have confused a few people, but once you have got to a quadratic in \( \cos x \) the solutions drop out nicely. 

The final question was very similar to the last question on the 2014 paper – in that it concerned minimising a function of the surface area of a 3D shape. Minimising it and checking the nature of the stationary point is straightforward and these marks could be picked up even if the candidate hadn’t managed to derive the expression for the cost of polishing themselves.

Overall a nice paper, a bit more challenging than some recent ones in places but generally it seemed pretty fair. They are liking simultaneous equations at the moment.

A scan of the questions is here and a pdf of my solutions (complete with my incorrect attempt of Q5b) available here.

I don’t actually teach Core 1, but as I’m trying to do every A level maths paper sat by students at my school I thought I’d post a few reflections after I had done it. A pdf of my solutions are here respectively.

Overall it seems to have been found pretty easy by the stronger candidates doing Further Mathematics but weaker candidates seem to have found it a bit more difficult. After having done the paper I think that it is fairly straightforward if your algebra skills are good, most questions are clear applications of clearly specified bits of knowledge.

Question 1 was just a bit of manipulation of surds, with the first part used in the second  with quite a nice rationalising the deonominator question. Question 2 was essentially a GCSE qustion – a 7 mark gift to people sitting this exam.  
 

Question 3 was a straightforward test of basic integration and differentiation skills. I think question 4 may have thrown a few people – when I first looked at it I thought I couldn’t do it – but as soon as you do the first part and find a few terms, finding the sum is straightforward. 

  Question 5 tests knowledge of the discriminant; I think the fact that the inequality you have to show is a greater than may confuse a few people, and when it comes to finding the set of possible values of p a lot of people will probably apply the quadratic formula instead of completing the square which is (as always) easier.

 
Question 6 is straightforward, nothing challenging there, they just have to do it. Question 7 I like  and is  straight forward when you consider the laws of indices – yet another easy quadratic to factorise. I think the final step may confuse people if they haven’t done something similar before. 

For Question 8  we have yet another quadratic that factorises (I’m getting a bit bored of these now…), and then a graph to sketch.  I still find it strange that identifying stationary points isn’t in Core 1.

Question 9 was a nice application of the formulae for arithmetic progressions. The last part did at least expect some thought on how to calculate the total which made it a bit more interesting.

  
Question 10 was probably the trickiest question, in my opinion, on the paper – the last part is certain to have thrown some people and required more thought than a simple “find the normal” paper. 

  
Overall I thought this was a very fair and accessible paper.

My students weren’t very happy with this years FP1 exam and found it harder than past papers. After doing the paper, I agree it seems harder than recent past papers but I think it was a fair paper.

Questions 1 and 2 I thought were incredibly straight froward (5 marks for factorising a cubic and solving a quadratic seems generous), though I was surprised and saddened that there was no Newton-Raphson in the numberical-methods section.  

Questions 3 and 4 were nice too, the summations in 3 dropped out quite nicely, and 4 was a straight forward test of basic definitions for complex numbers.

Question 5 concerned the hyperbola, and wasa nice test of the basics of finding normals and points of intersection – not much to trip people up here I didn’t think.

There were two induction proofs for question 6 (no divisibility question though, which everyone I have spoken too seemed pleased about. I feel that these were a bit trickier than similar induction questions in previous years, with the algebraic manipulation to complete step 3 being not as straightforward (in that you couldn’t immediately factorise out some of the terms for the summation proof, for example) as sometimes.

I would describe Question 7 as a gift of a question. I can’t really believe they explicitly asked youto find the inverse of the matrix B, before it needed to be used to work out the coordinates of the triangle T. I think this should eliminate the possibility of candidates using the wrong matrix in this question.

  
Oddly this paper had only 8 questions, I have got used to the FP1 exam having 9.  The final question was however worth 14 marks and was trickier than a lot of conics questions. I guess the main reason that it seemed trickier was due to the wording of the question and the fact that the last part of the question wasn’t splt into multiple sections. Once you got past the wroding and the similarity of the letters p and q I thought this was quite a satisfying question, and I liked the result you were asked to show in the last part.

Please excuse the strange coloured triangles across the photos, it seems to be an odd artefact of the Office Lens app. 

Update: Click here to download a pdf of my solutions and here for a scan of the questions. 

This post was going to be more involved…. 

Last week a few of us were sharing photos of our collections of maths books and for some reason I couldn’t post more than one photo on a tweet! So, I said I’d write a blog post – I was originally going to write about about some of my favourites, but being short of time tonight I think I will leave that and some of them may make it into my “Classic Maths Books” series. 

My books are seemingly spread all over various book shelves, and some just haven’t made it on to shelves (or I have let people borrow them and when they have come back their shelf space has been taken by something new) so below are photos showing all (I think) of them:

I think I may catalogue them over half term as there are quite a few here I had forgotten that I had…

Are there any that people would recommend I get etc?

I do think it would be good to have a central review of books and some of the nice things they contain or a lending system to spread our collective libraries around. 

This Saturday I went to a great session organised by the East Midland’s branch of the Association of Teachers of Mathematics. It was led by Colin Foster of The University of Nottingham who was talking about “Rich Mahematics from Closed Questions”.

Writing about the session in a no-linear fashion I liked how he used Fermat’s Last Theorem as an example of a yes-no question (often seen as a closed question) leading to rich mathematics.

  
A closed question is often defined as a question with one correct answer and no scope for discussion. The open vs closed question idea is something that is discussed often, with closed questions being seen as inferior to openquestions and not readily leading to rich mathematics.  The aim of this session was to show that rich mathematics can come out of closed questions.

I liked the initial question of \( 15 \times 823 \). This works out to be 12345. I think this could be a nice launch point for a lesson, looking at other similar sums, divisibility rules etc.

Colin then made the point that two closed questions together or a sequence of closed questions can be a good prompt to some interesting maths. He first gave two quadratics \(x^2+7x+6\) and \(2x^2+7x+6\); both of these quadratics can factorise. Then the prompt questions could be things like “Is this a fluke?”, “What can we say about how to make these?”. I confess I haven’t figured this out yet, so will probably write about it when I do.

As an example of a sequence of questions consider the following:

• How many factors does 10 have?
• How many factors does 100 have?
• How many factors does 1000 have?
• How many factors does 10000 have?

I started by manually listing factors, and soon noticed a pattern of the square numbers appearing. It becomes much clearer when you realise that \(10 = 2 \times 5 \), \(100 = (2 \times 5)^2 = 2^2 \times 5^2 \), \( 1000 = 2^3 \times 5^3 \) and so the factors can be computed using a two-way table

  
There are many opportunities for students with this task including practise at finding factors, spotting number patterns, predicting future terms of the sequence, generating nth term rules and investigating how the factors of other sequences grow (for example 6,60,160,1600 and 2,4,8,16,32). Of course not everyone in the class will reach the same point, but this isn’t a problem. I really liked Colin’s justification for doing these kind of activities:

“The emphasis is on the thinking going on in the classroom, not on the kids getting to the final answer” 

This is a nice “low floor, high ceiling” task and I’m going to use it for an observed lesson later this week, and I will blog about the lesson in full towards the end of the week.

I also realised (something that in hindsight I should have known before as it is obvious) that any prime number to the the power of \( n \) has \( n+1 \) factors.
After looking at factors, Colin presented some inequalities to shade (see his paper here for more information – it’s a nice short article!) and a few problems about fitting rectangles into squares.

All in all it was a great session (it was also good to catch up briefly with Rob who is the secretary of the East Midlands Branch) and the £5 cost is a bargain.

It also reinforced the fact that I have always been irritated by the open/closed questioning distinction. An open question can just as much lead to narrow mathematics as a closed question – it’s the questioner (is that a word?!) that is important.