I’m finally getting the material from my session online – if you want an overview of #mathsconf5 last sturdy check out my post here.
In this post I am aiming to share the materials I handed out in my session “How to Enjoy (and Succeed at) Your NQT Year”
I’ve embedded my Prezi below, if you were at my session you would know that I didn’t get anywhere near through it.
[prezi id=”http://prezi.com/-dz30jtfabtw/?utm_campaign=share&utm_medium=copy&rc=ex0share” align=center width=600 lock_to_path=1]
All the materials can be accessed on my website at the links below:
I started the session by finding out the strengths and weaknesses of attendees. In my opinion you will have a good understanding of these by the time you start your NQT year (even if you are an ITT student I think you often know what they will be before you have spent much time in the classroom). For me, my strength is that I am pretty good at stretching the high attainers whereas I see behaviour management as a weakness as this is something that I have had to work quite hard at to get where I am now. Being frank with yourself about your personal qualities is very important if you want to improve and develop your practice.
Following this we talked about behaviour management strategies; I was very interested in some of the conversations happening about the use of reward lessons in the computer room for good behaviour amongst other things. My top tips for behaviour management is to ensure that you are always consistent (however tired and fed up you are) and follow through with any sanctions you hand out. It is very easy to let things slide as term goes on – especially in the winter months when it is dark and cold – try your best to not let that happen.
Moving on to lesson planning I talked about my five key things to consider when planning a lesson:
- The big picture.
- The key learning objectives.
- 5 key questions.
- Any possible misconceptions.
- How will you assess learning.
For me the questioning used with the class and individual learners is the most important thing to bring on the mathematics of students by prompting them to think critically about it. This fits in nicely with a school focus on questioning in my school which is good. Our new Year 7 scheme has questions for most lesson plans. I think considering questions before the lesson means that I think more in depth about the maths that I am presenting and how it will come across to learners. The same can be said for considering misconceptions; some of the best questions in my opinion will draw out misconceptions and enable us to tackle them head on as a class. I was possibly a little controversial in this section by saying that I don’t really like the assessment being on lesson plan pro-formers. This is not because I don’t think it is important – it is of course crucial to know where your students are with the topic of a lesson! My point here was that I don’t want how I am going to assess my students (which is really my problem to resolve) to affect how they experience the mathematics that we are doing that lesson and so my mode of assessment shouldn’t be a focus of the lesson planning process.
Many teachers now have to move rooms between lessons. When this is the case I find that it helps to have some go to starters that don’t require me to have logged on to a computer and turned a projector on. For this reason, this year I have stuck a sheet with some easy “no-plan” starters into the back cover of all of my lower school student’s books. I have written a bit more about this in my post “No Plan Starters”. With practice I find that the students don’t need too much guidance if I just tell them a starter task (and maybe write a few numbers on the board) and it means that they are practising some basic skills while I am waiting for the computer to load.
Before I was planning on discussing the advantages/disadvantages of technology in lessons I talked about homework. My guiding principle is the I want a homework that takes the minimum amount of time to prepare and mark but that gives the maximum possible benefit to the students. A type of homework that fits this bill are the PRET homeworks as shown below.
I particularly like the research and stretch components of this style of homework. I found that last year, being very precise with the expectations for the first couple that I handed out meant that students soon learnt what was expected when I gave them a homework in this style. Before you go away and write some you should definitely check out Jo’s (@mathsjem)and Kathryn’s (@DIRT_expert) PRET homework website as there are plenty already to use!
For technology in the classroom I was going to talk about different tech tools so I think I shall write about this topic more over the next few months….
I had a large section planned entitled “Do Some Maths”. This is actually my number one tip for your NQT year! It is all too easy to get caught up in the mundane tasks of a teacher that you don’t spend time doing any maths apart from the questions you need for lessons. I’m sure that most of us chose to teach maths because we love doing maths so I think it is important to spend some time doing maths that is challenging. Here is a nice question:
A particularly nice source of challenging problems is the book “Calculus for the Ambitious” by T.W. Kernel. This is a book targeted at strong A-Level students giving a more university-like approach to Calculus than you see at A-Level.
Your NQT year is an ideal time to develop your subject specific pedagogic knowledge. Use those extra frees to go an observe other teachers focussing in particular on how they teach a given topic. Look for how they structure a lesson to build understanding gradually, how they tackle topics that are perceived as being hard to teach and how the activities they choose promote confidence in the learners. Another excellent way to build your subject knowledge (both pedagogic and general mathematical) is to join at least one, if not more, subject associations. Personally I am a member of the ATM and the IMA and value the access this gives me to their journals. On the education journal note it is definitely worth getting involved in the #mathsjournalclub discussions that I organise – the next one is on the 19th October, see here for more information.
On the subject of marking, which is often seen as a necessary chore, and any time you spend doing it should have an impact – it definitely should not take over your life. Kev Lister’s (@listerkev) RAG123 marking has revolutionised the way I mark. Being able to get quicker feedback from the students is really helpful, it doesn’t take that long to get through a set of books commenting if necessary. I do a deep mark in line with my schools marking policy in addition to this, but having looked at the books so much these deep marking sessions are much quicker than they would have been.
I believe that having a network of teachers you can turn to for advice outside of your own department and school is incredibly helpful. Twitter makes this easy, so spend some time on twitter and take part in as many twitter chats as you can. I provide a summary of all the maths specific chats here.
My plan was to end on giving some tips for your NQT year from people other than me:
- Don’t do any work on a Saturday.
- Follow up on sanctions – but make sure they are fair.
- Always stick to class routines that you set.
- Don’t be afraid to say when you are struggling – someone will help you.
- Laminate resources.
- After a bad lesson find a positive – even if it is that you kept all the pupils in the room.
- Always remember the good pupils and how much you enjoy teaching them.
- Write any advice given to you down.
- Divide your time away from school into working time and non-working time and stick to it.
- Talk to anyone and everyone.
- Don’t overdo it
and then mention a few things to avoid including listening to people moaning all the time and working all the time.
The main thing I have learnt myself from this session is to not plan as much!! Thanks to Danny Brown (@dannytybrown) for his interesting points in the session and to Rob Beckett (@RBeckett_Yd) for having a quick look over the slides previously and giving me an NQT’s perspective on them.
 Alex opened his talk with a logic puzzle that he had featured in one of his early Guardian Puzzle blog posts: Find the odd one out in the symbols below
Alex opened his talk with a logic puzzle that he had featured in one of his early Guardian Puzzle blog posts: Find the odd one out in the symbols below  This puzzle was orignally due to Tanya Khovanova who had written about it here. It is intended as a piece of fun to emphasise the intrinsic issue of odd-one-out puzzles. Namely, that they tend to be focussed around a particular way of thinking (Alex provides a nice example in his post) when in fact many could be seen as the odd one out for different reasons. In the puzzle above, the odd one out is actually the one on the left hand side by virtua of not being able to be called the odd one out – an interesting philosophical dilemma there!
This puzzle was orignally due to Tanya Khovanova who had written about it here. It is intended as a piece of fun to emphasise the intrinsic issue of odd-one-out puzzles. Namely, that they tend to be focussed around a particular way of thinking (Alex provides a nice example in his post) when in fact many could be seen as the odd one out for different reasons. In the puzzle above, the odd one out is actually the one on the left hand side by virtua of not being able to be called the odd one out – an interesting philosophical dilemma there!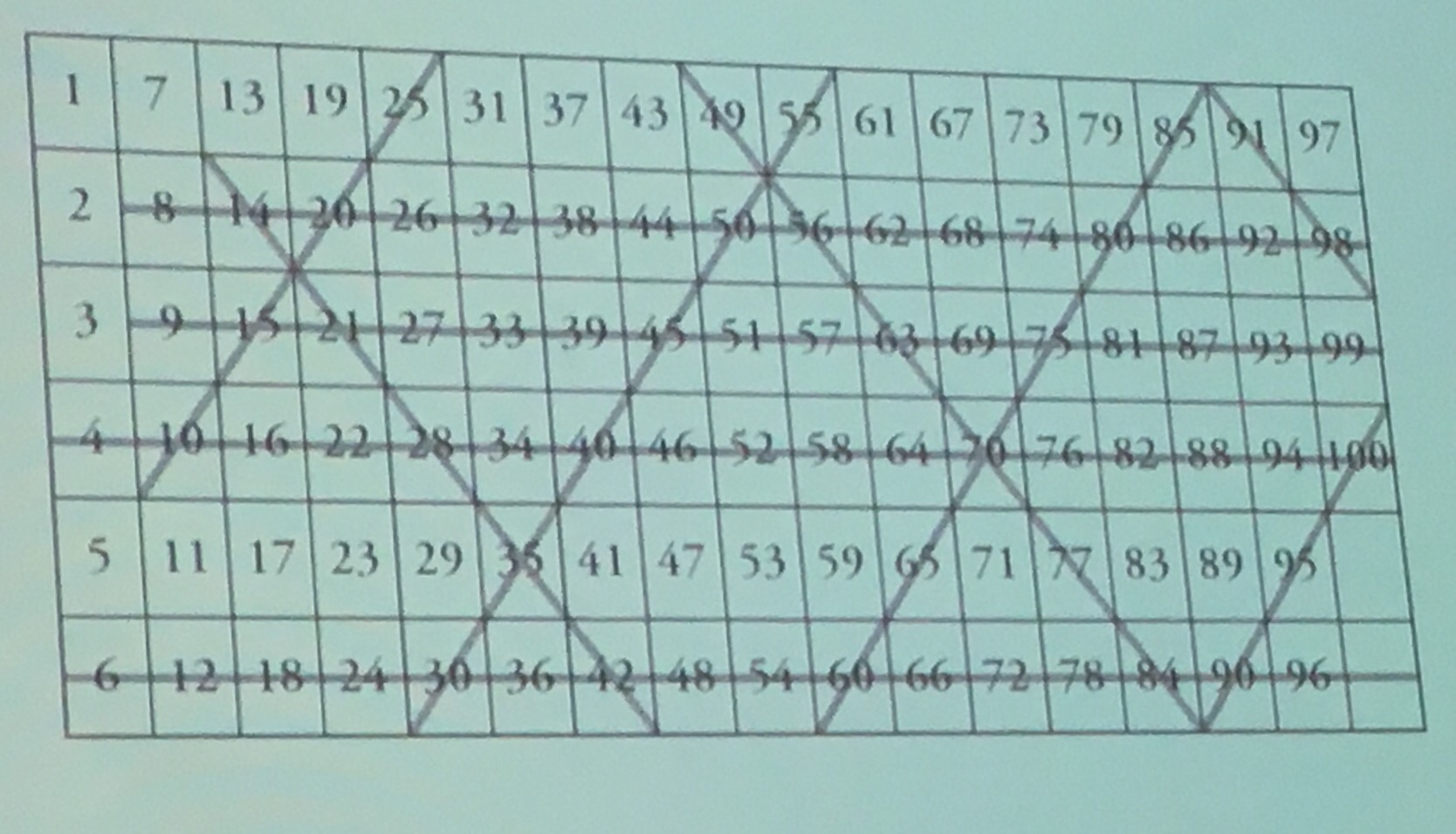 He then described the Ulam Spiral, devised by Stanislaw Ulam where numbers are arranged in a spiral and primes highlighted generating a pattern where primes lie on diagonal lines. I’m going to write some MATLAB code to generate these I think and write a bit more about them in the future.
He then described the Ulam Spiral, devised by Stanislaw Ulam where numbers are arranged in a spiral and primes highlighted generating a pattern where primes lie on diagonal lines. I’m going to write some MATLAB code to generate these I think and write a bit more about them in the future.