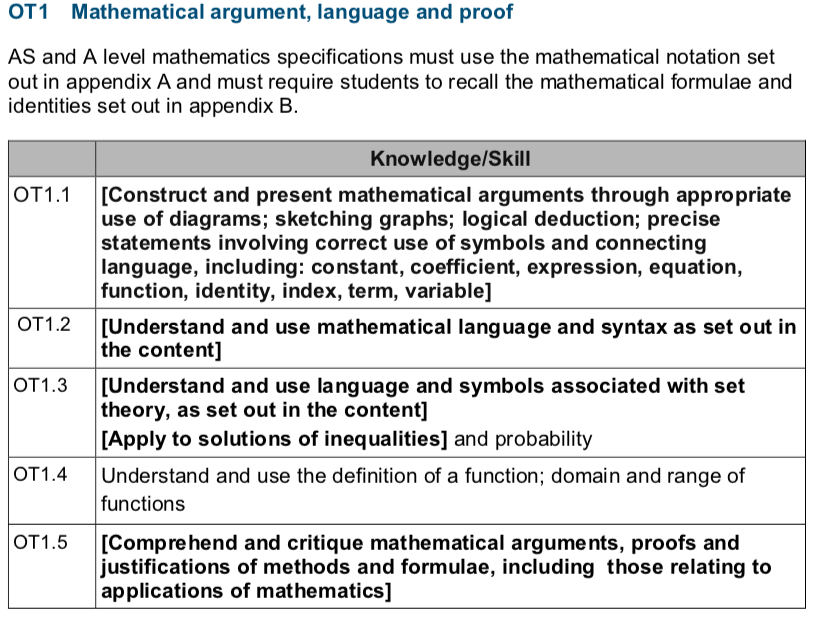
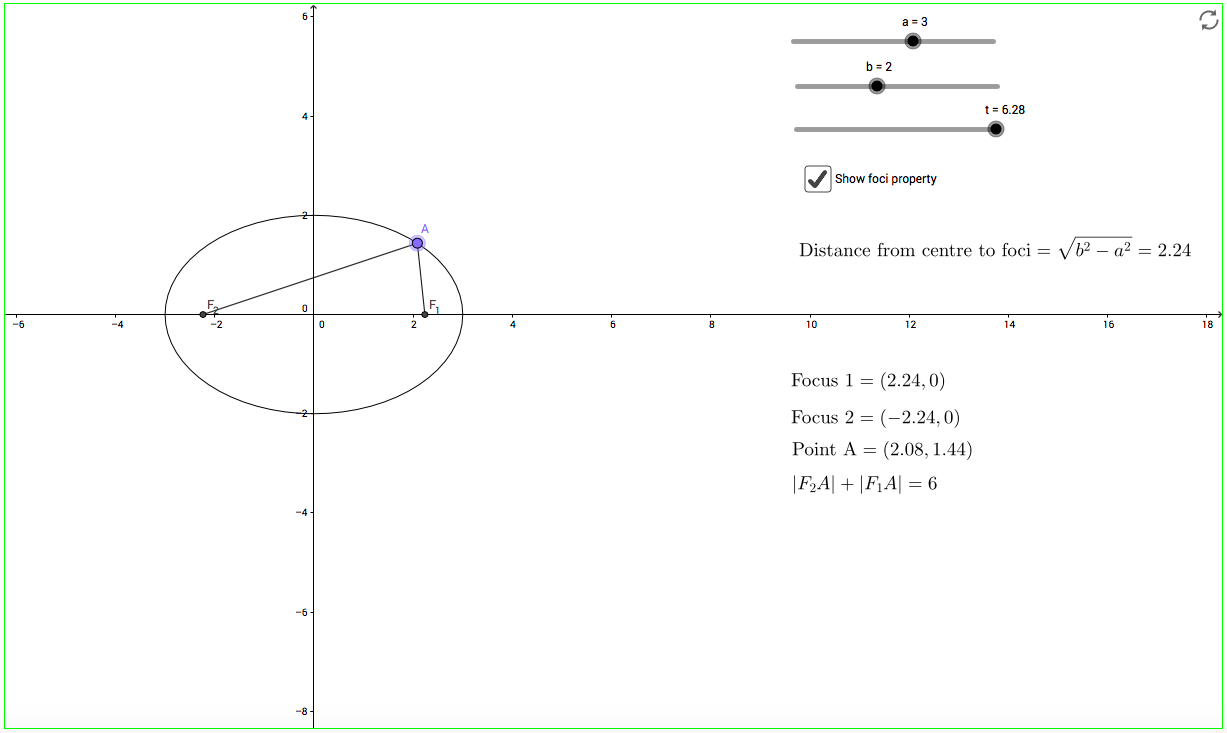
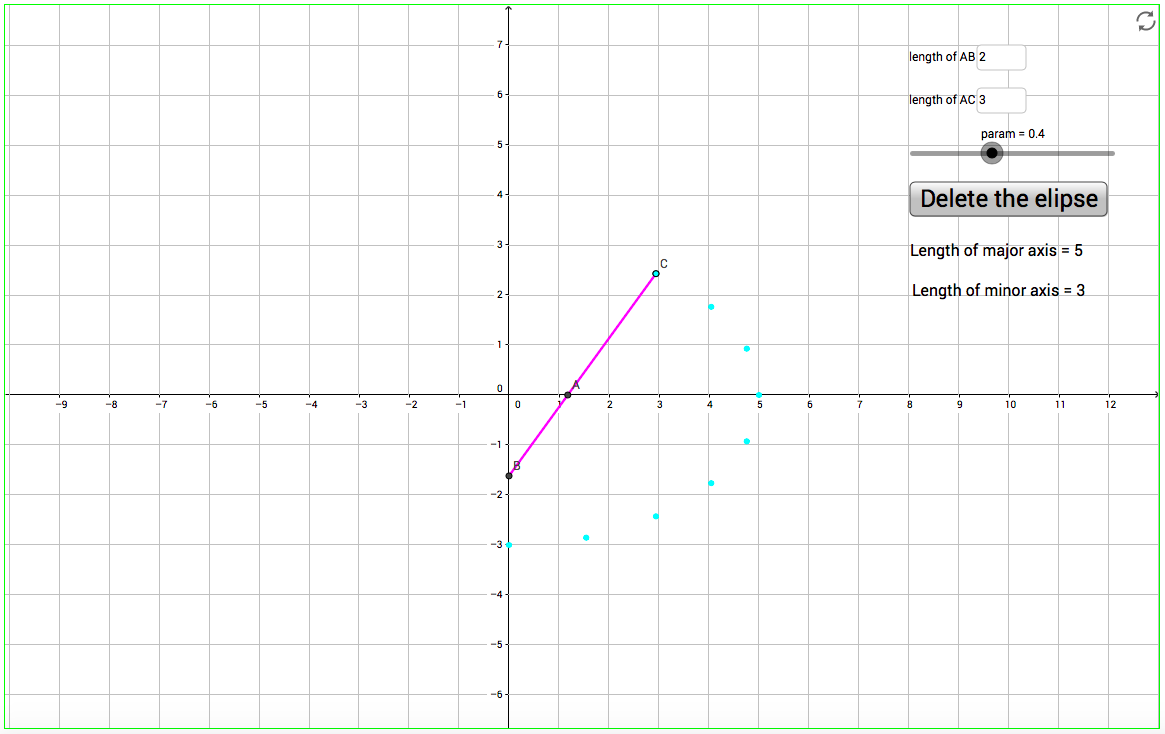
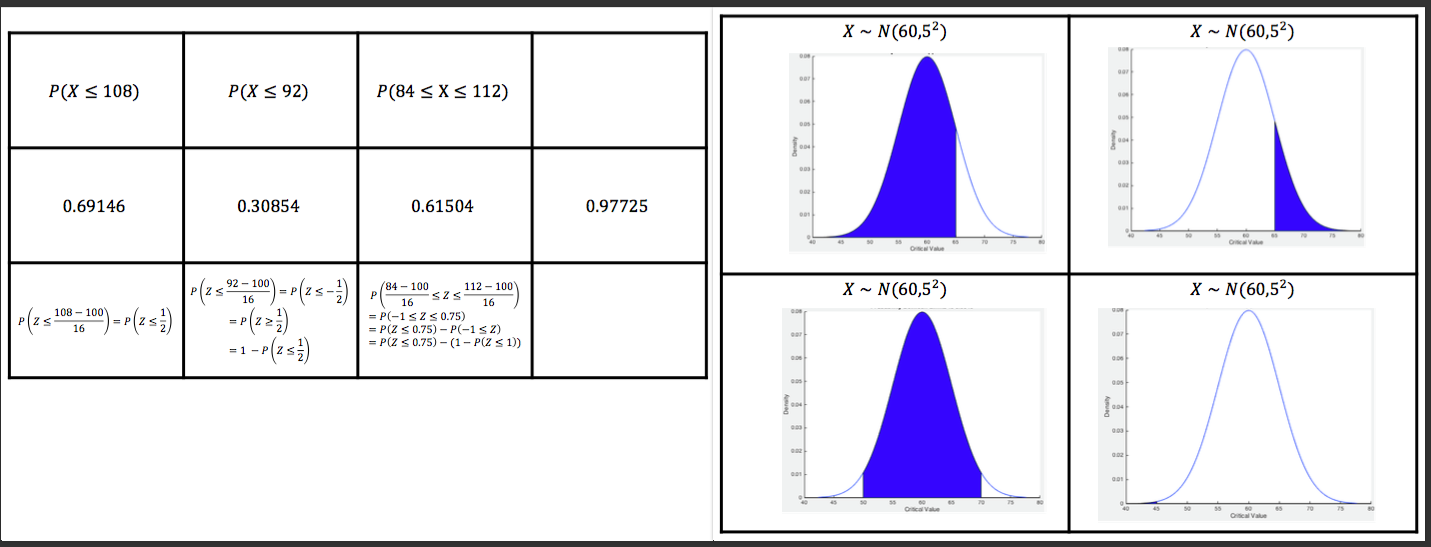
One of the things I have missed since teaching in a school is the fact that I don’t have access to Matlab….
Matlab is a product from The Mathworks, designed originally for numerical computation (indeed the name derives from MATrix LABoratory as the software was originally focussed towards operations on matrices) but which now is capable of much more. More information about Matlab and The Mathworks is available here.
I had got used to using Matlab in teaching an demonstrating, not least because of the ease with which you can use it to check matrix computations, plot graphs of functions and demonstrate numerical methods.
Last term I set my Year 12 Further Mathematicians some homework which involved them researching the Jacobi Method and performing 2 iterations of this method on a \(2 \times 2\) matrix system. I wanted to be able to demonstrate this straightforward numerical method to them, without having to work out how to use the Python IDE on the Windows computers at school, so I decided to give Matlab Mobile a try.
Matlab Mobile was originally released in 2010 (see here for an early blog post discussing Matlab Mobile) but I hadn’t had much reason to use it before. Originally the app needed to connect to your computer with a running copy of Matlab, but since it’s release it has become a lot better. Th app is currently on version 4.1.1 which is a universal app suitable for both the iPad and the iPhone. With this version (as long as you have a valid Matlab Licence for desktop) you can connect to a copy of Matlab running in the cloud to execute commands. You can also upload your files to the cloud so that they can be run from the app.
On opening the app you are presented with a screen that looks like this:
The left hand portion of the screen displays commands that you have typed and on the right hand side you can toggle between Figures and viewing your command history.
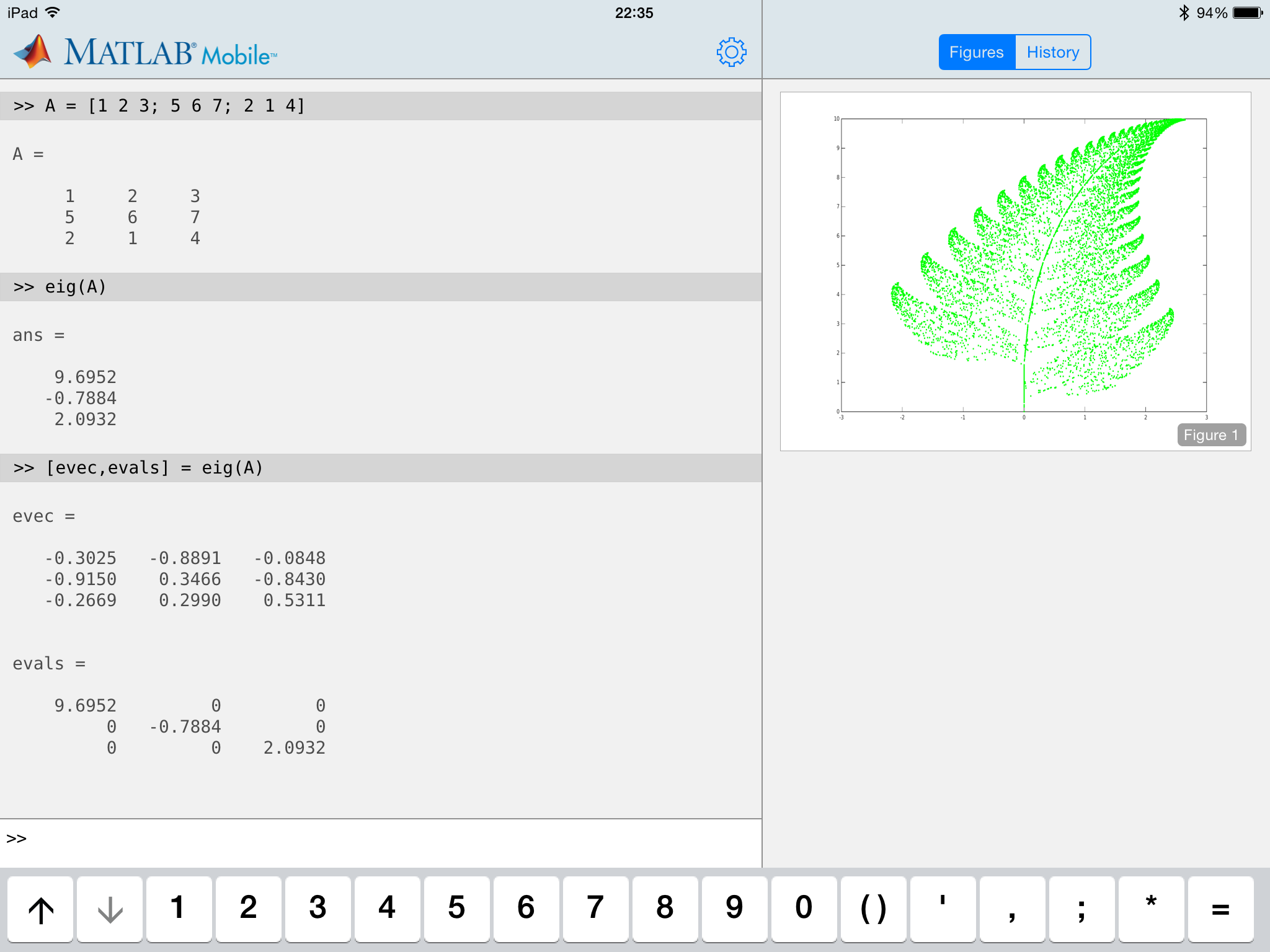
Using a keyboard (I recommend using a bluetooth keyboard here as the on screen keyboard takes up so much space) it is easy to type short commands that accomplish complex things. For example, in the screen shot below, I create a matrix and then find its eigenvalues using the eigs command. As you can see this command can also return the corresponding eigenvectors of a matrix simply by explicitly giving two output arguments to the function.
One of the great uses of the Matlab desktop product is to prototype functions before coding in another language. Unfortunately, the mobile app does not allow you to edit or create .m script files or function files. This is a real shame, especially as it extends to the inability to make small edits to files you have already stored in the cloud. Luckily though, you can at least view the test of functions that you have written by using the command type in the command window, as shown below.
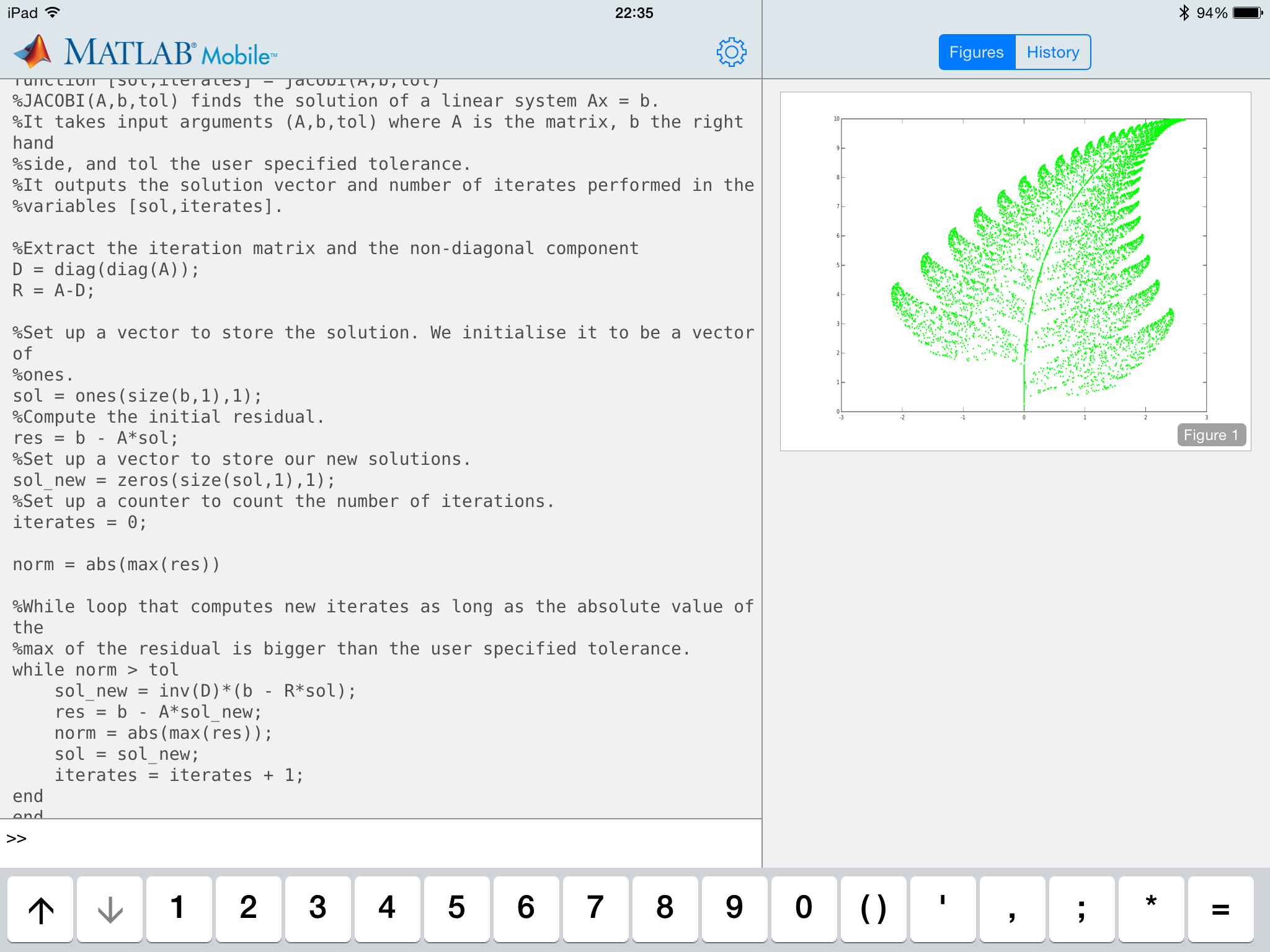
The code shown above is a naive implementation of the iterative Jacobi scheme for solving systems of linear equations – I stress it is not the most efficient way to code this algorithm, but it is clear for teaching purposes. Using Matlab Mobile I was able to discuss this short function with my class, and relate it to the algorithm that they had to research and then express in pseudocode.
If you are going to use Matlab Mobile for a similar purpose I would recommend avoiding writing script files and instead use function files with enough arguments to allow you to vary everything you will want to demonstrate the affect of. I would also say it is probably useful to print more of the internal workings of the function to the command line than you would normally.
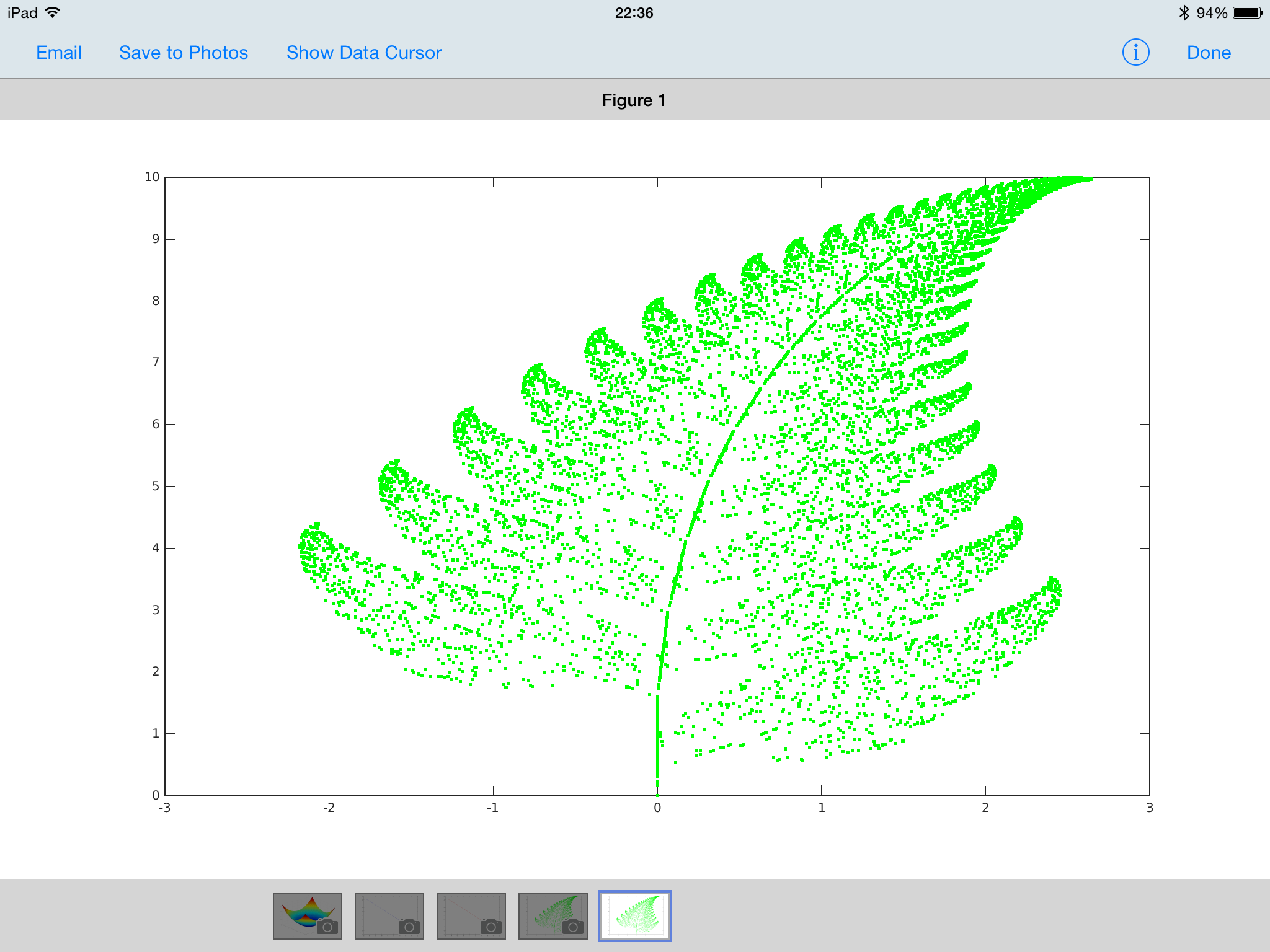
Another great piece of functionality in Matlab is the ability to produce professional looking graphs with very little effort. You can still generate figures such as the one below (a visualisation of the Barnsley fern after 10000 iterations – I may write a blog post about this in the future) in the Cloud, but a lot of the data exploration tools in the figure window of the desktop product are not usable. You can however, save the figure to your camera roll or email it to yourself.
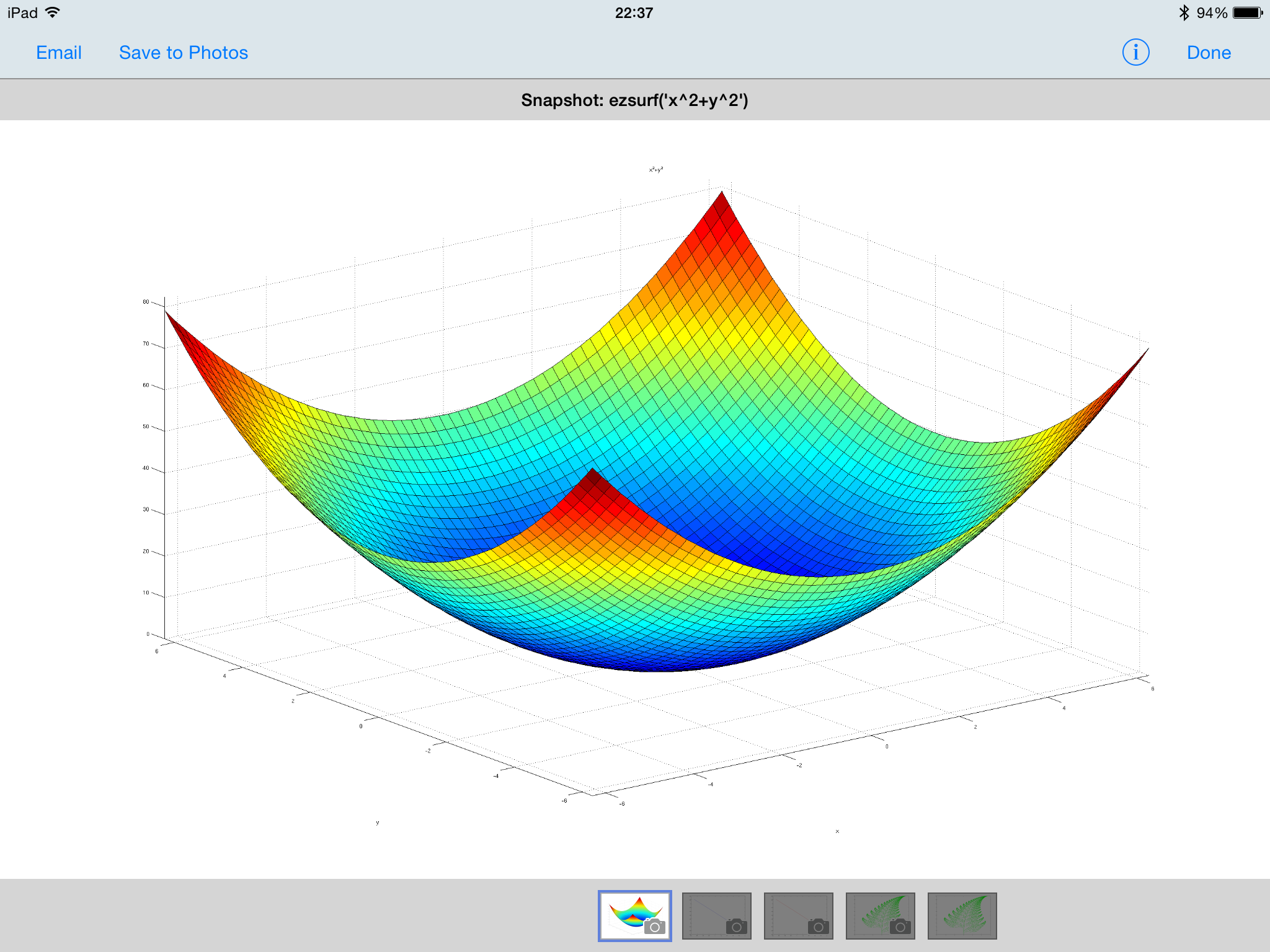
As a final example of the graphical abilities of Matlab Mobile the 3D surface plot below was created using 4 lines of code.
One important thing to note is that I couldn’t connect to the Matlab Cloud through my schools wifi (I suspect because of the firewall) and so had to resort to using my phone as a 4G hotspot.
All in all, if you have a Matlab licence it is well worth familiarising yourself with the Mobile app, and I managed to do all that I wanted to do in the classroom with it. I just needed to do a bit more forward planning than I would have done if I had had access to the fully fledged Matlab product! Hopefully as the app develops they will remove some of the limitations that are currently present.