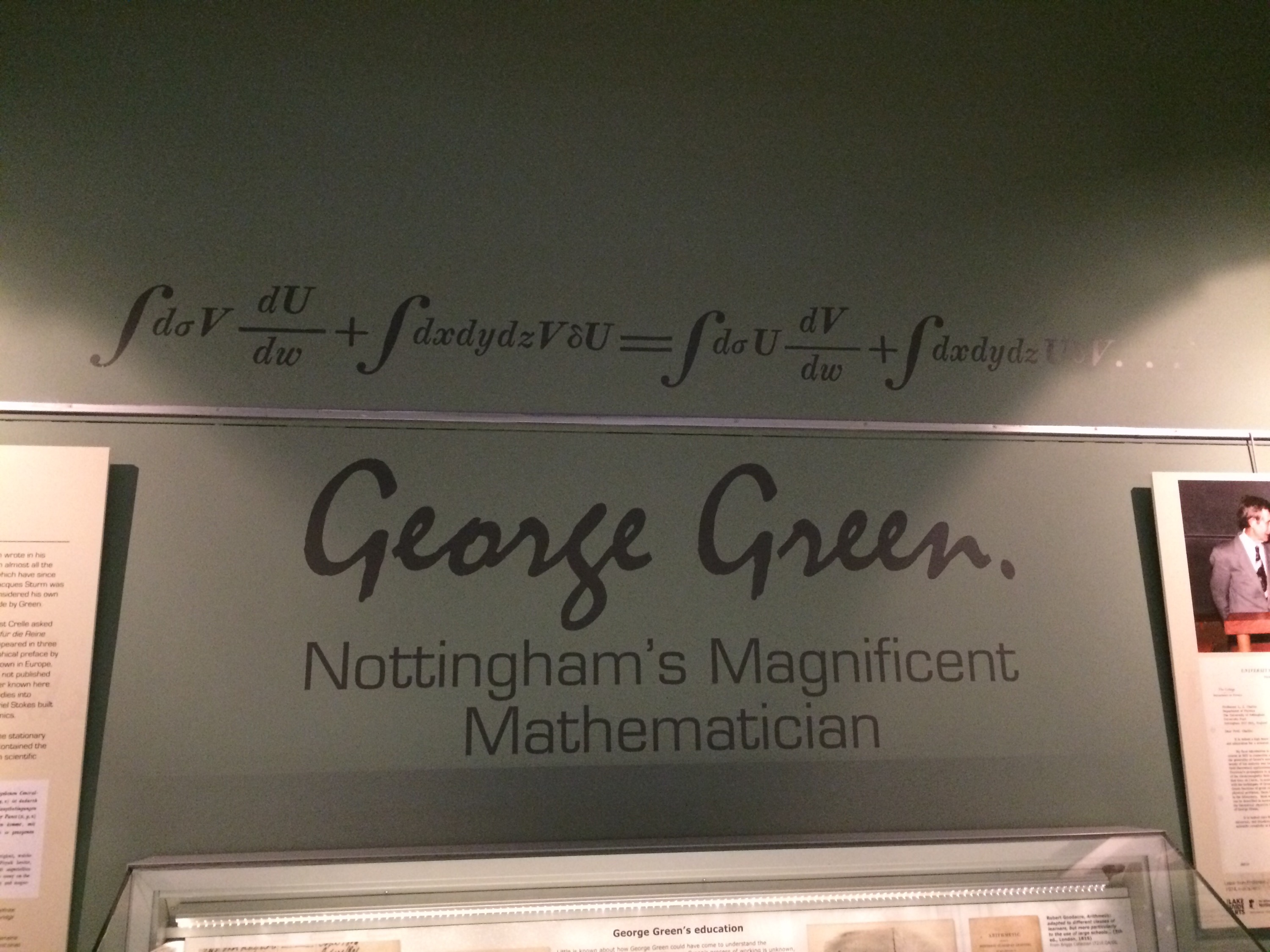This is a post that I should have written months ago when this exhibition opened. Unfortunately it is closing on Sunday, it’s open 12pm-4pm tomorrow and Sunday, the details are available here. If you are local to Nottingham and have some spare time it is well worth a visit.
George Green is probably one of Nottingham’s most famous residents. The science library of The University of Nottingham is named after him. He was a miller based in the Sneinton area of Nottingham, he had little formal education but published a paper (by subscription) in 1828 where he presented the following theorem, given below in modern notation.
Green’s Theorem
Let \( R \) be a simply connected plane domain whose boundary is a simple, closed, piecewise smooth curve \(C\) oriented counter-clockwise. If \( f(x,y) \) and \( g(x,y) \) are continuous and have continuous first partial derivatives on some open set containing \( R \), then
\( \int_C f(x,y) \mathrm{d}x + g(x,y) \mathrm{d}y = \int \int_R \left ( \frac{\partial g}{\partial x} – \frac{\partial f}{\partial y} \right) \mathrm{d} A
\)
This theorem has had wide ranging influences, but at the time received limited exposure due to the local nature of the publication and it not being published in a scientific journal.
An interesting fact about this paper is that Green used Leibniz’s notation for the calculus as opposed to Newton’s notation which was in common usage in England at the time.
If you want to learn more about George Green the following two videos are a good place to start:
Maths history trail of Nottingham – George Green
Sixty Symbols – George Green