In a fairly shameless copy of the style of some of @srcav‘s posts where he solves a maths problem and briefly goes through his reasoning I have decided to do the same with some (easier) problems that I have recently discovered.
The Further Mathematics Support Programme (FMSP) have produced a series of 6 posters of problems that should be accessible to GCSE students. The first one of which is a fairly nice area problem – the poster is available here and shown below.
As always, when solving any kind of geometric / visual problem I find drawing a diagram (even if there is a printed one in front of me) helpful, and I then mark on everything that I already know.
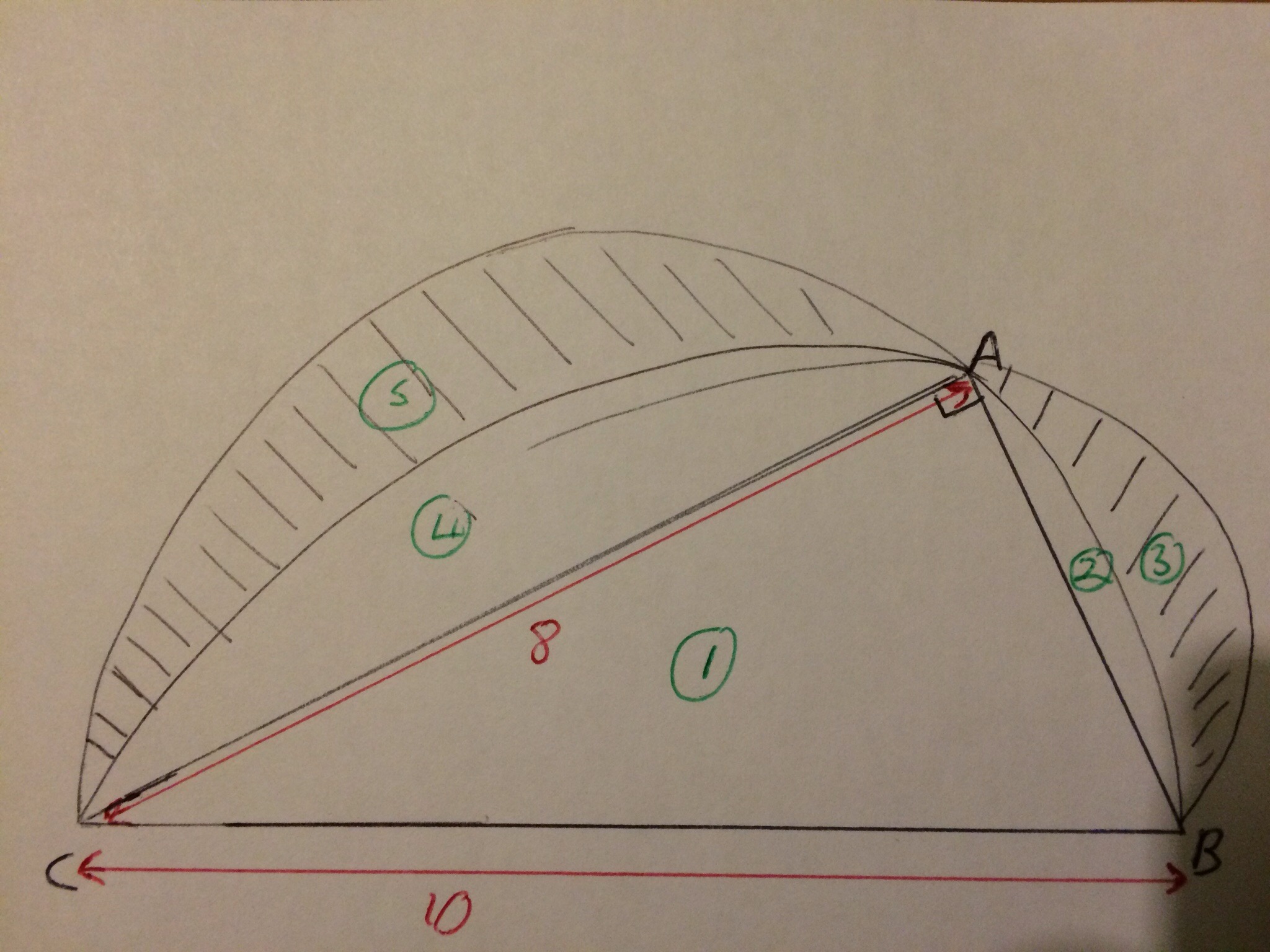
Each distinct area I have labelled with a number (maybe lower case letters or greek letters would have been a better choice, but never mind!) and I now proceed to write down as much as I can quickly calculate. Here, that involves a bit of Pythagoras’ theorem and the formulae for working out the area of a right angled triangle:
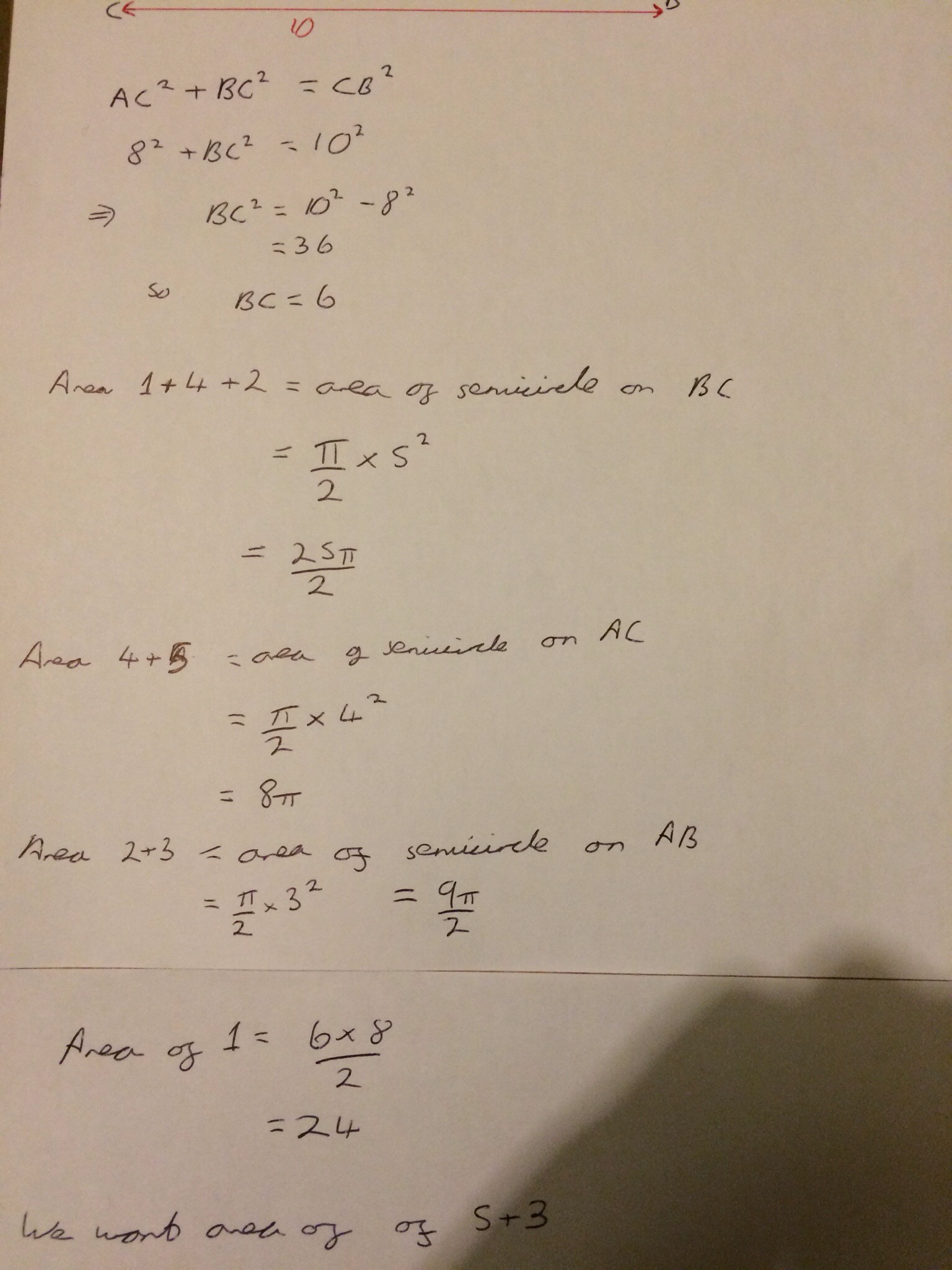
Now comes the slightly harder bit, where I actually had to think and work out how I could find the shaded areas that I was interested in using only what I had already worked out. It was actually fairly easy, as soon as I had written some things down!!
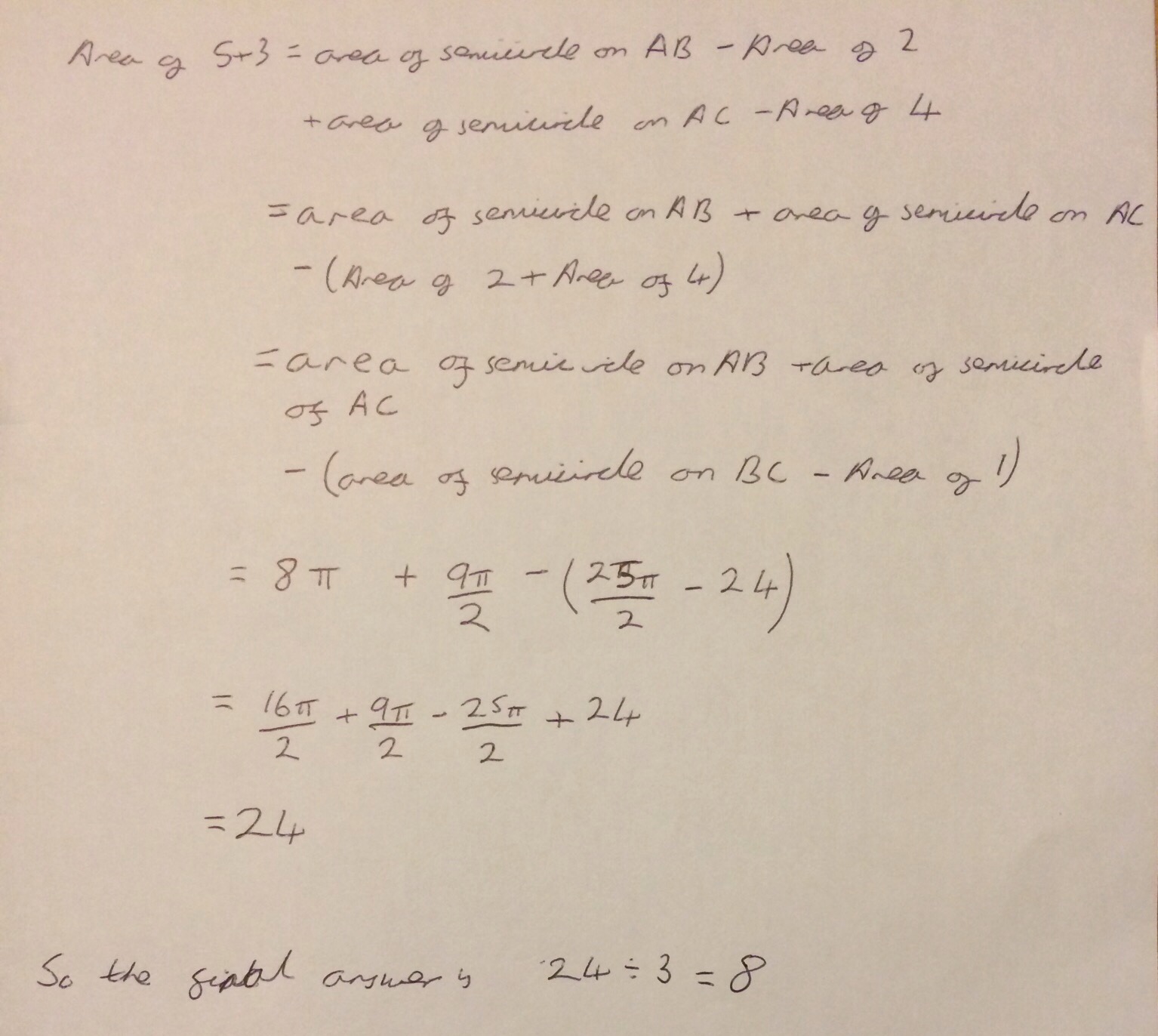
The result is lovely, in that the area of the shaded regions is the same area as the triangle
Overall, I think this is a nice, accessible problem that would get students to think.
As, an aside this problem demonstrates (though it isn’t immediately clear from the picture) the fact that Pythagoras’ theorem can be extended for other shapes attached to the sides of a right angled triangle – in this case semi-circles.

One reply on “FMSP Favourite Problems – Number 1”
A solution
Area of lunes = area of triangle + area of semi-circle on b + area of semi-circle on c – area of semi circle on a.
Area of lunes = area of triangle.