Here is the second post in my ‘FMSP Favourite Problems’ series looking at the problems selected for the Further Maths Support Programme’s favourite problem series of posters.
This second problem I’m not very keen on as it just seems a bit dull.

As usual I started with a small sketch, annotated with what I knew – that fact that at every bounce the ball rebounds to a height 75% of the previous bounce.
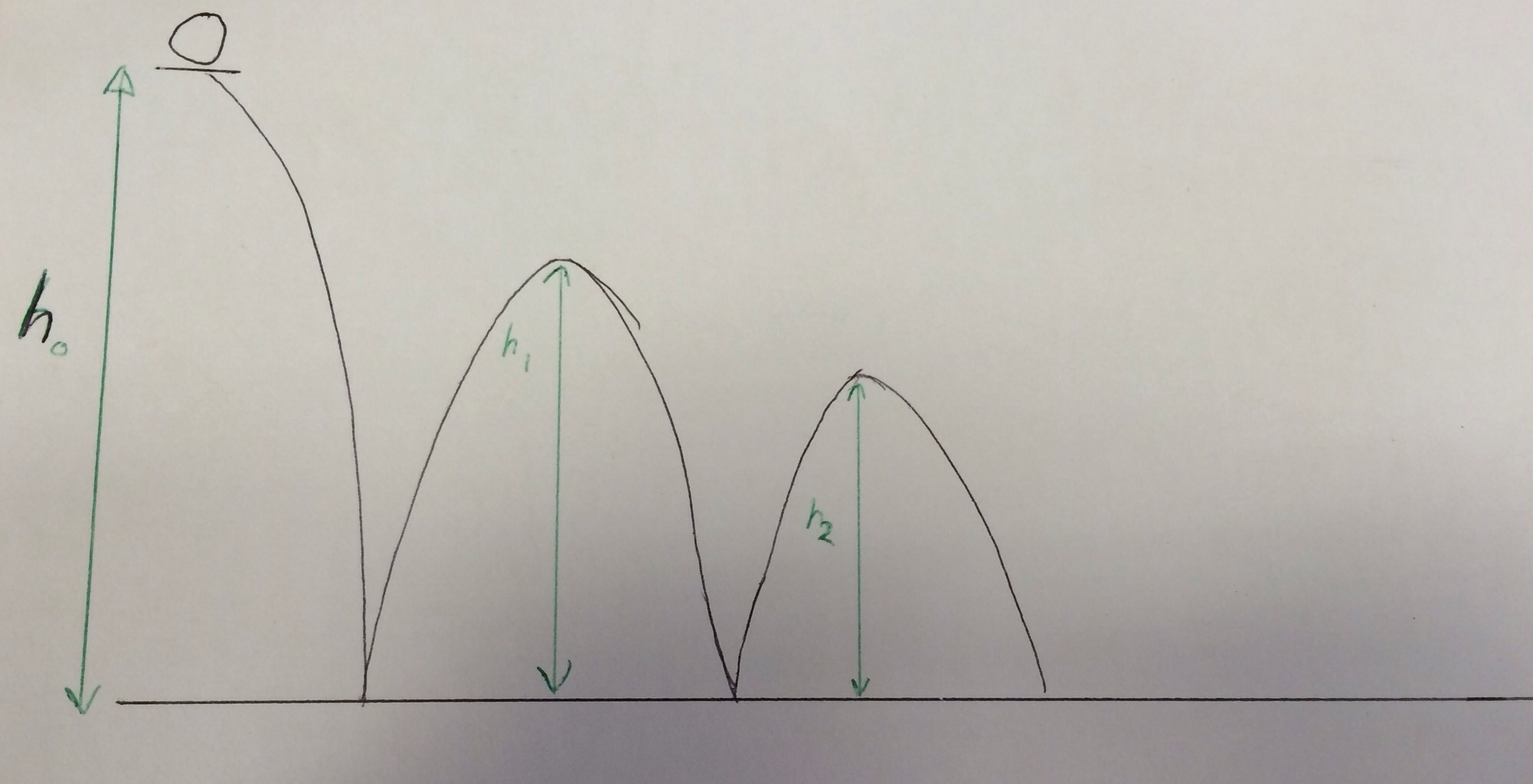
As this is repeated for every subsequent bounce you can easily obtain a relation between the height of the initial bounce and the height of the \(nth\) bounce:

Clearly this is easily solved using logarithms
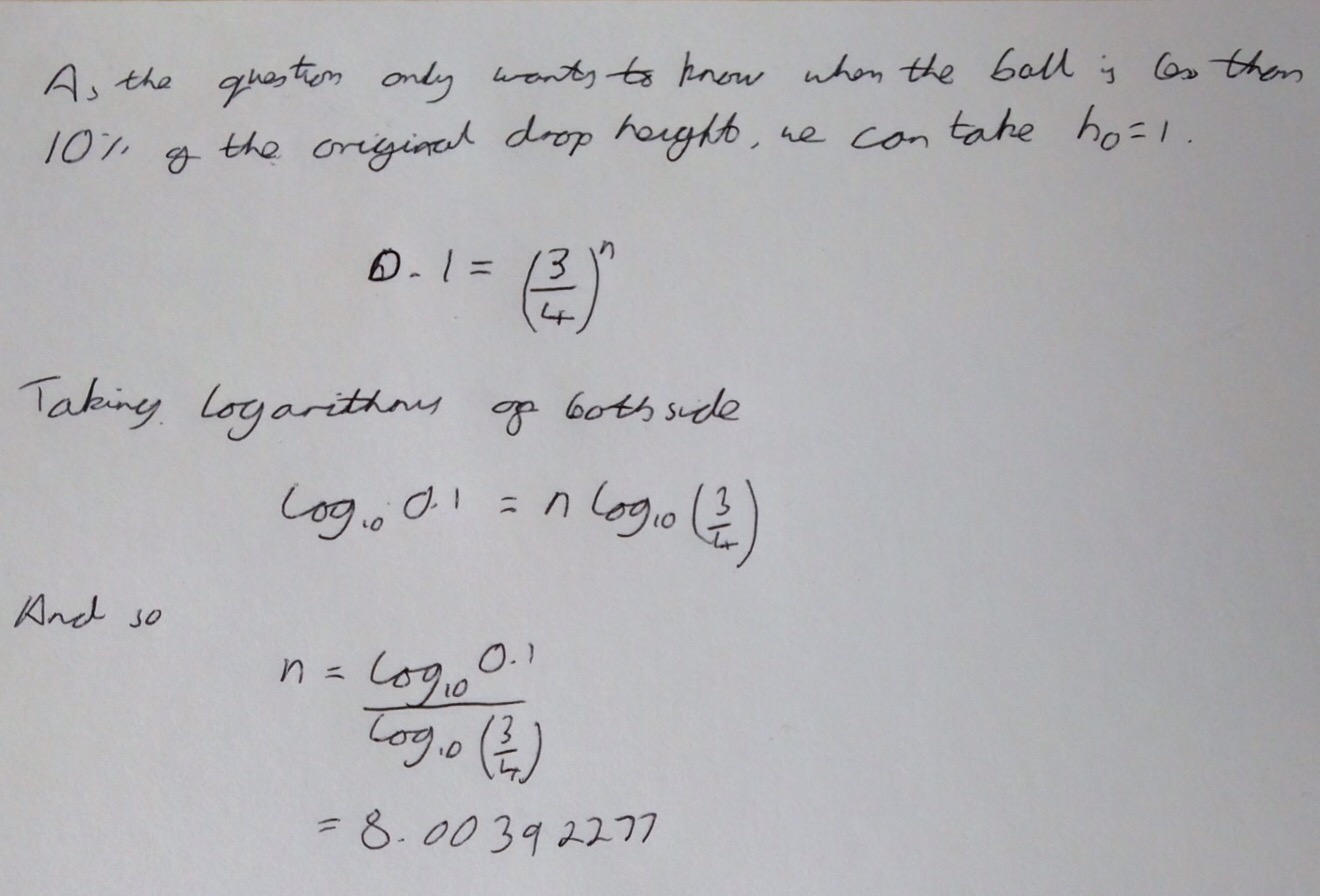
The answer above isn’t the full answer, since you don’t have decimals of a bounce, the ball must be on the 9th bounce before it rebounds to less than 10% of the original height.
Unfortunately, the typical GCSE student will not have come across logarithms – though I sort of feel that logarithms should be in the GCSE syllabus – and so couldn’t solve it this way. Unless I have missed something obvious, the only way that they could solve it would be to either calculate the powers of 0.75 until they got the correct value or to plot a graph. Not wanting to plot a graph by hand, I quickly loaded Matlab on my iPad and plotted the following:
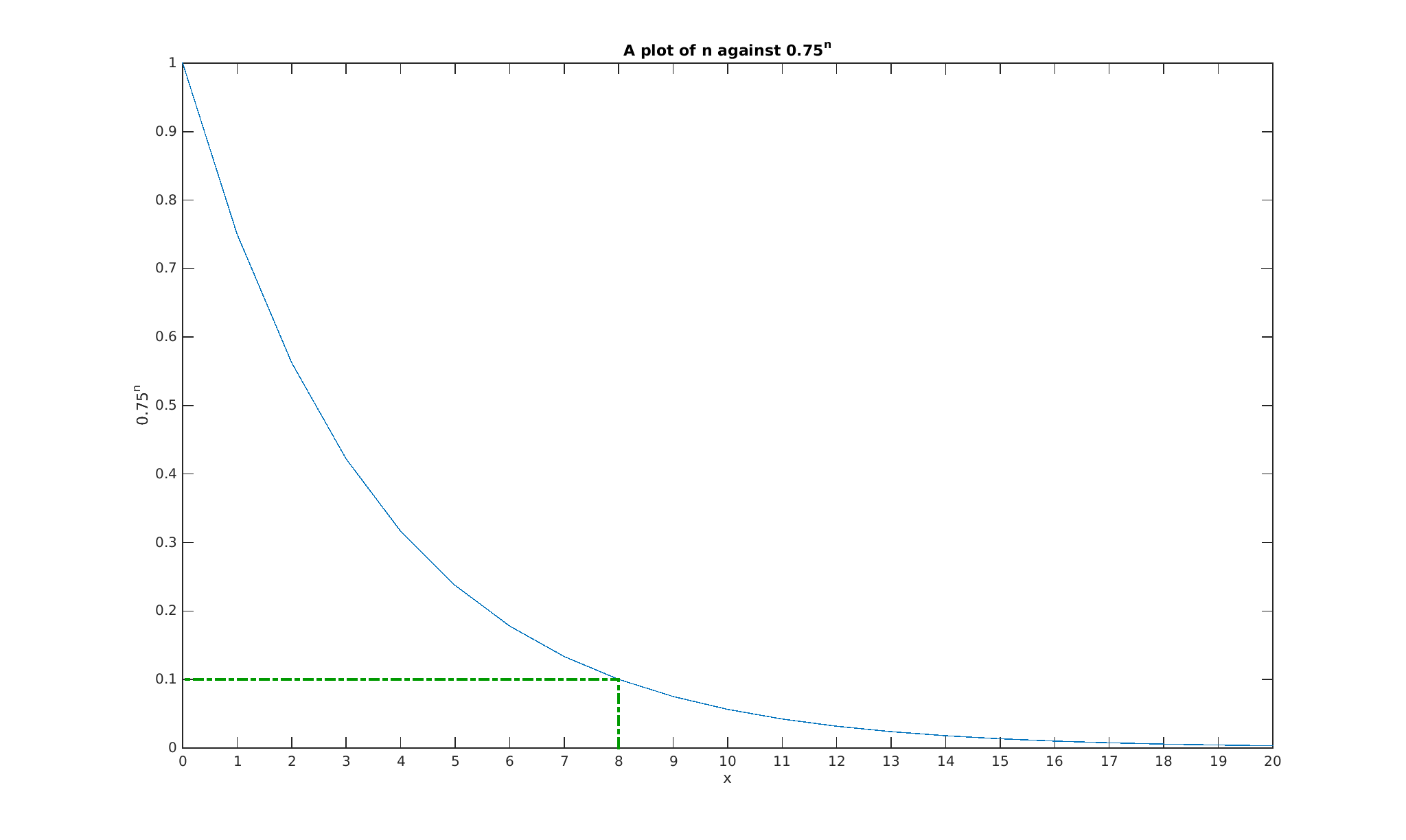
In conclusion, as a problem I don’t find this particularly satisfying, however I think it could be used as an opening to an interesting lesson discussing exponential decay, mathematical modelling, ensuring answers you report are meaningful and interpreting graphs.
One reply on “FMSP Favourite Problems – Number 2”
Nice post, I like this as a problem to solve with logarithms, but agree its not great for the GCSEs.