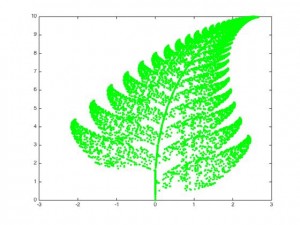
Barnsley’s fern is a mathematically generated image that resembles the Black Spleenwort fern as shown below
This fractal was first described by Michael Barnsley in his book Fractals Everywhere in 1993. It is surprisingly easy to generate and is an example of an iterated function system. It is based on randomly applying one of four affine transformations.
\( \begin{align} f_1(x,y) &= \begin{pmatrix} 0.00 & 0.00 \\ 0.00 & 0.16 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} + \begin{pmatrix} 0.00 \\ 0.00 \end{pmatrix} \\ f_2(x,y) &= \begin{pmatrix} 0.85 & 0.04 \\ -0.04 & 0.85 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} + \begin{pmatrix} 0.00 \\ 1.60 \end{pmatrix} \\ f_3(x,y) &= \begin{pmatrix} 0.20 & -0.26 \\ 0.23 & 0.22 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} + \begin{pmatrix} 0.00 \\ 1.60 \end{pmatrix} \\ f_4(x,y) &= \begin{pmatrix} -0.15 & 0.28 \\ 0.26 & 0.24 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} + \begin{pmatrix} 0.00 \\ 0.44 \end{pmatrix} \end{align} \)
The initial point is set to be the origin, and subsequent points are generated by applying one of the above four transformations. Which transformation is chosen probabalistically – the probabilities are \(0.01,0.85,0.07\) and \(0.07\) for \(f_1,f_2,f_3\) and \(f_4\) respectively.
I wrote two (basic) functions in Matlab, one to generate the points and then one to plot them.
A video (generated using Matlab) showing the growth of the fern is below:
Here is the Matlab code I used to generate the video – it takes a relatively long time to run as it plots each frame separately.