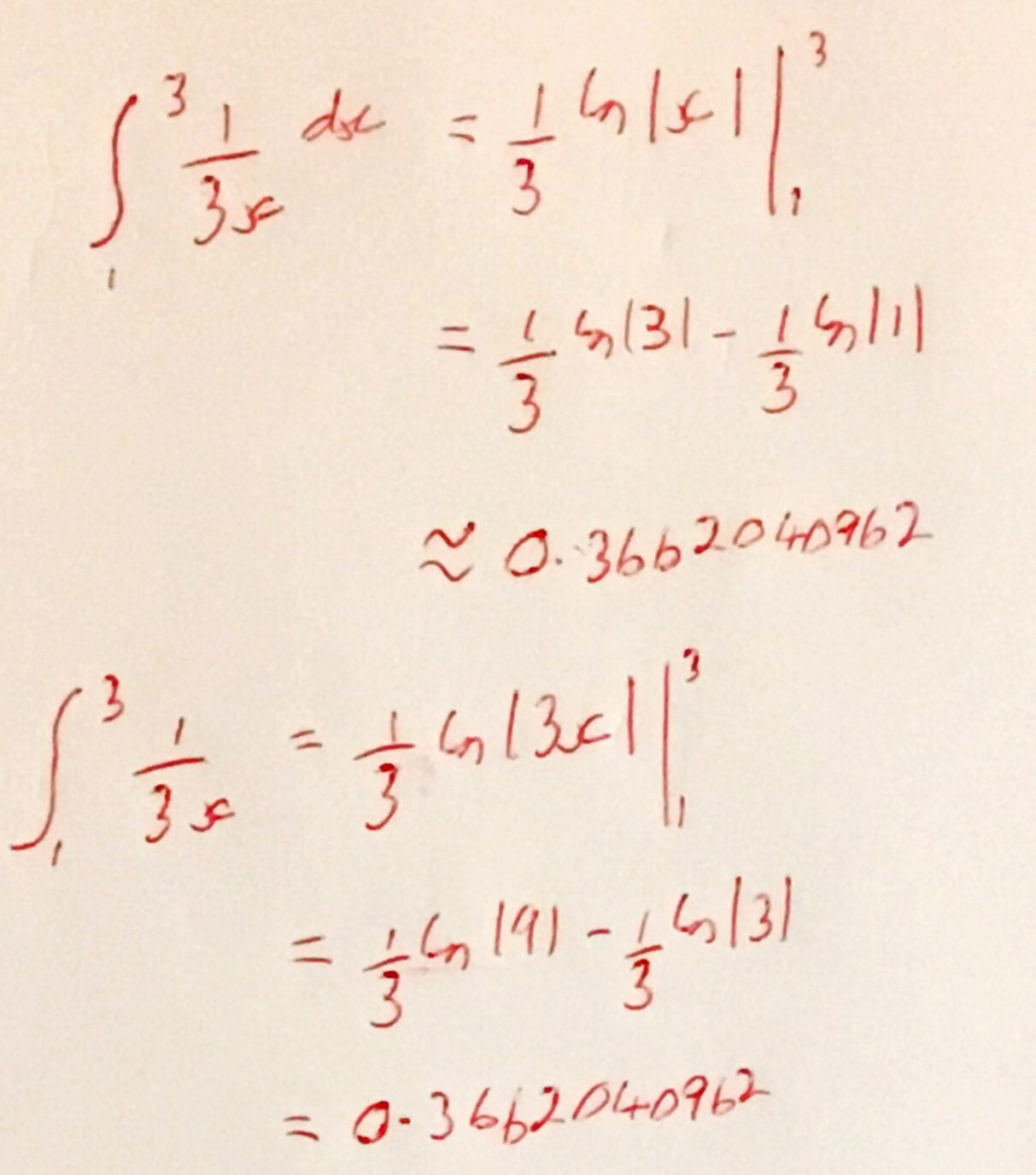I was recently asked about the integration of \( \frac{1}{3x} \), this had come up in the solution of a differential equation. More specifically the fact that there are multiple ways to integrate this:
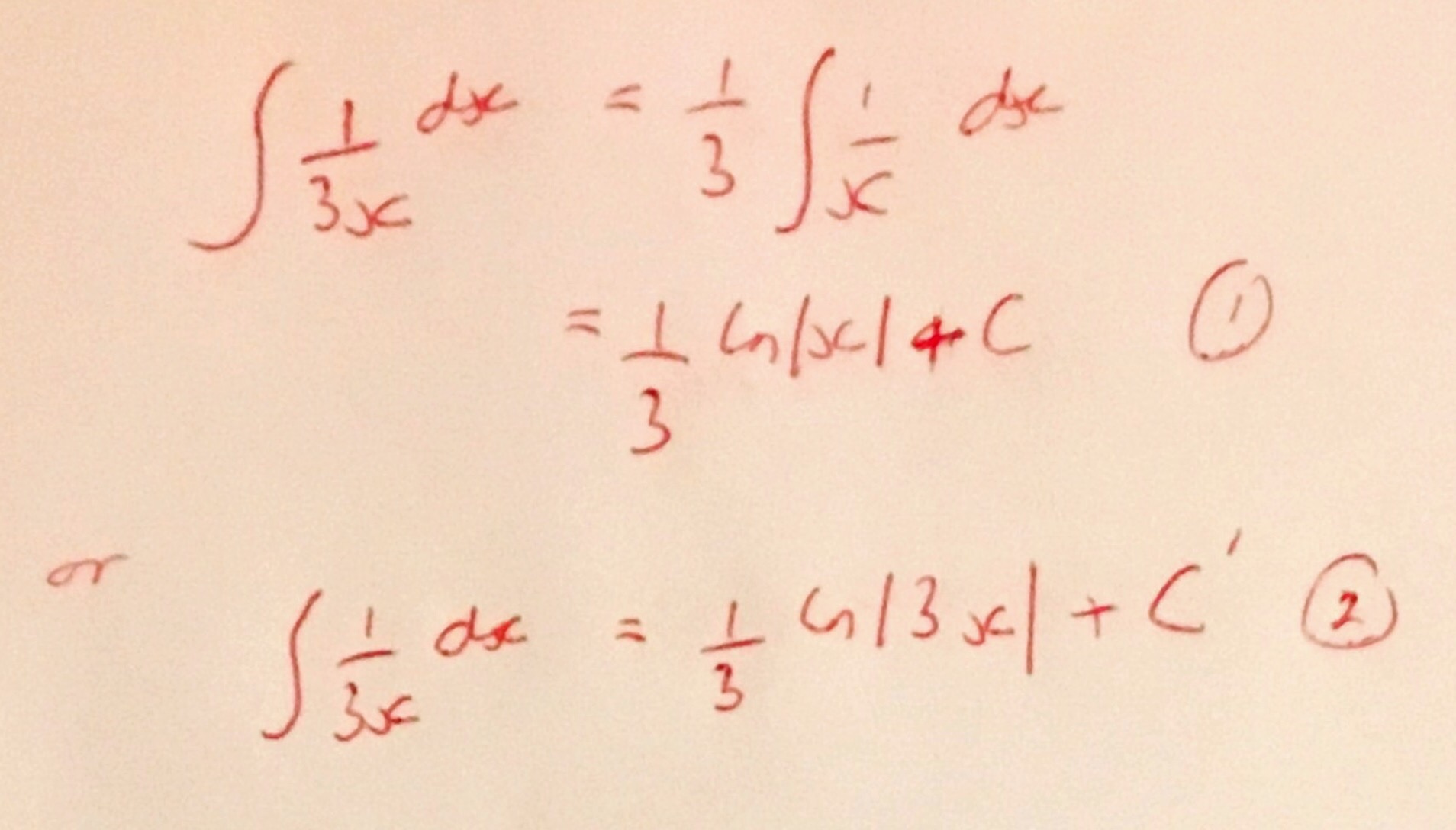 At first glance these do not appear to be the same, however plotting them suggests that they are part of the same family of solution curves.
At first glance these do not appear to be the same, however plotting them suggests that they are part of the same family of solution curves.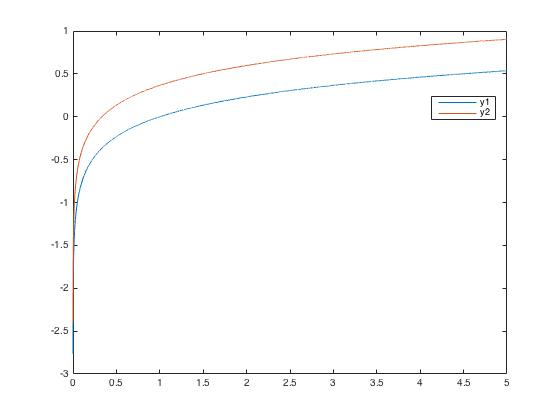
Indeed a simple manipulation of the constant of integration shows them to be the same functions apart from the addition of a constant.
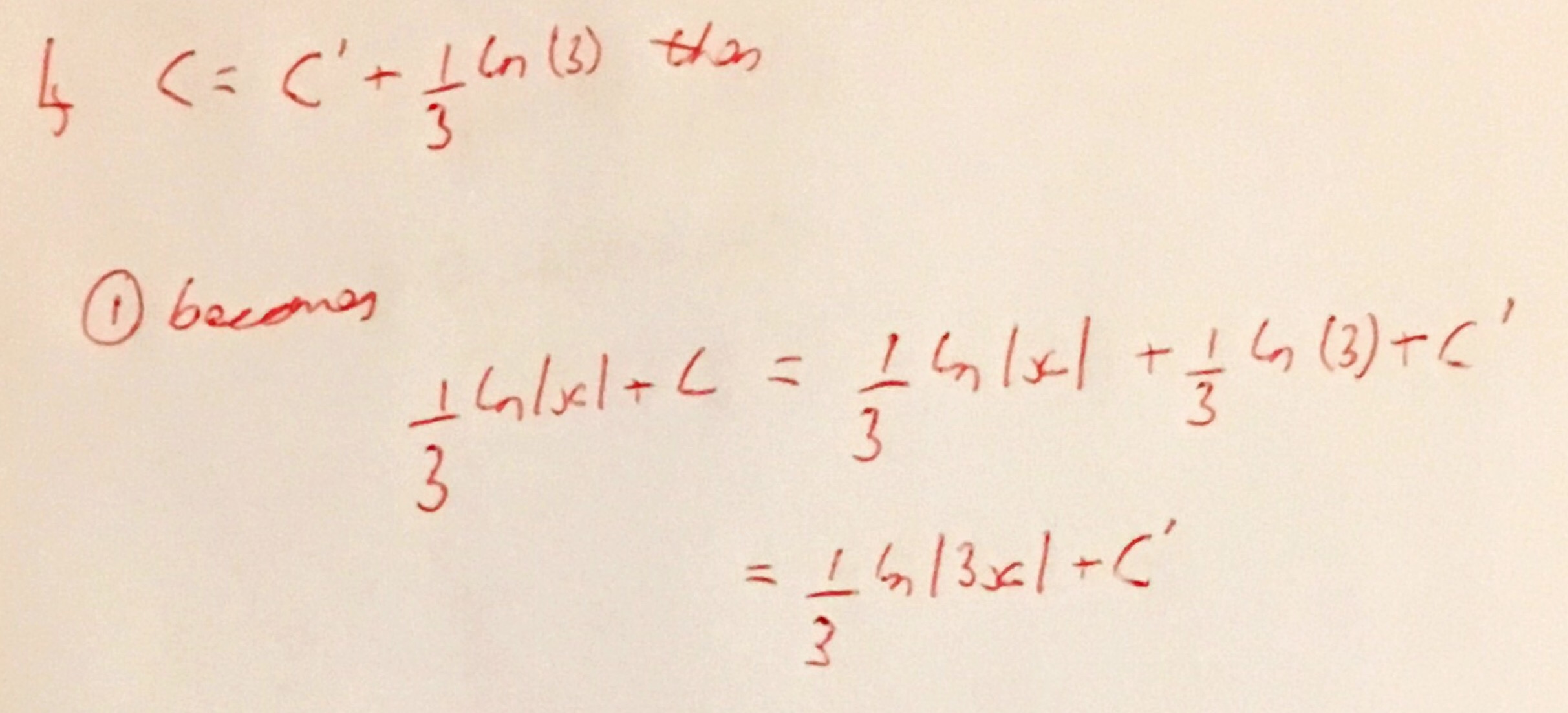 Of course these constants would be fixed by an initial condition, and so both versions of the integration would lead to the same solution of the differential equation.
Of course these constants would be fixed by an initial condition, and so both versions of the integration would lead to the same solution of the differential equation.
I have a vague memory of having this confusion myself when I was an A-Level student, but since then I haven’t really thought about this as I always “pull any constants outside of the integral” before integrating.
Thinking about this a bit more, I think that a great question for students would be to ask them to explain why \( [(1/3)\ln (x)]_1^3 = [(1/3)\ln (3x)]_1^3 \). I’m sure many would just evaluate the integrals as shown below, but asking for an explanation could lead to a deep discussion about the nature of the logarithm function.