Session 1 – An Introduction to Probability Distributions, Terry Dawson
I decided to attend this session as I wouldn’t describe Statistics as one of my strengths.
I use Geogebra quite a bit but I have never used the probability calculator option before. It works well on the iPad edition as you can see below, and provides a really nice interface for visualising probabilities and calculating them.
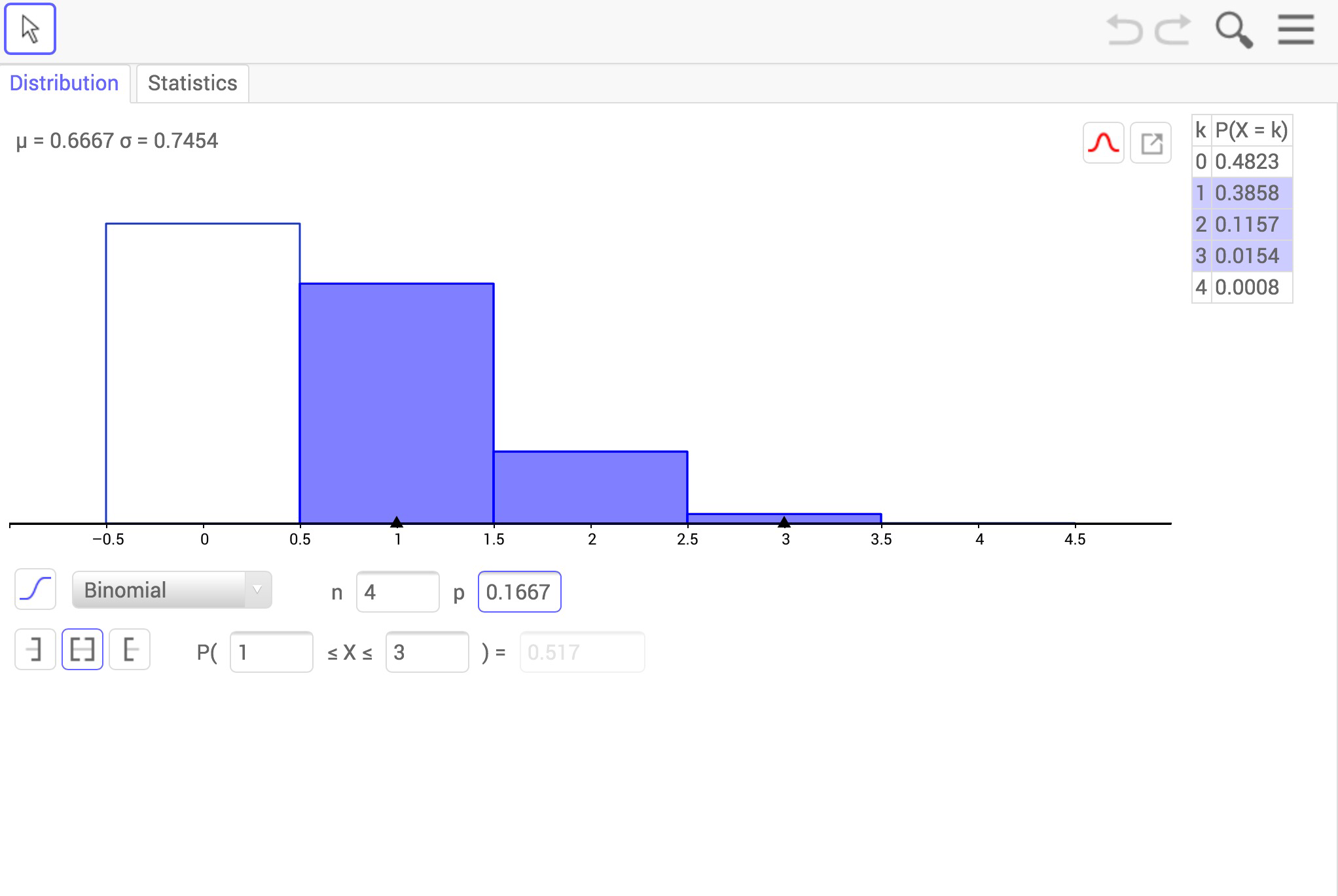
There was an emphasis on linking the teaching of the binomial distribution to the teaching of the binomial expansion. I do this, but I like the idea of making it explicit to students by getting them to do a dice experiment and relate the outcomes to the binomial distribution. The experiment suggested was to roll a dice 4 times and count the number of fives that occur. these outcomes could then be tallied up and you could also construct a tree diagram. Then you could relate the branches of the tree diagram to the number of occurrences of \(p^4, p^3q, p^2q^2,pq^3,q^4\). One resource that I particularly liked from this session was a card sort linked to the following article from the Daily Mail:
- “A study has found that 41 per cent of Britons admit to regularly using their phones, tablets and eReaders when sat on the loo.” “Smartphones were identified as the preferred gadget of choice, cited by 65 per cent of respondents”.
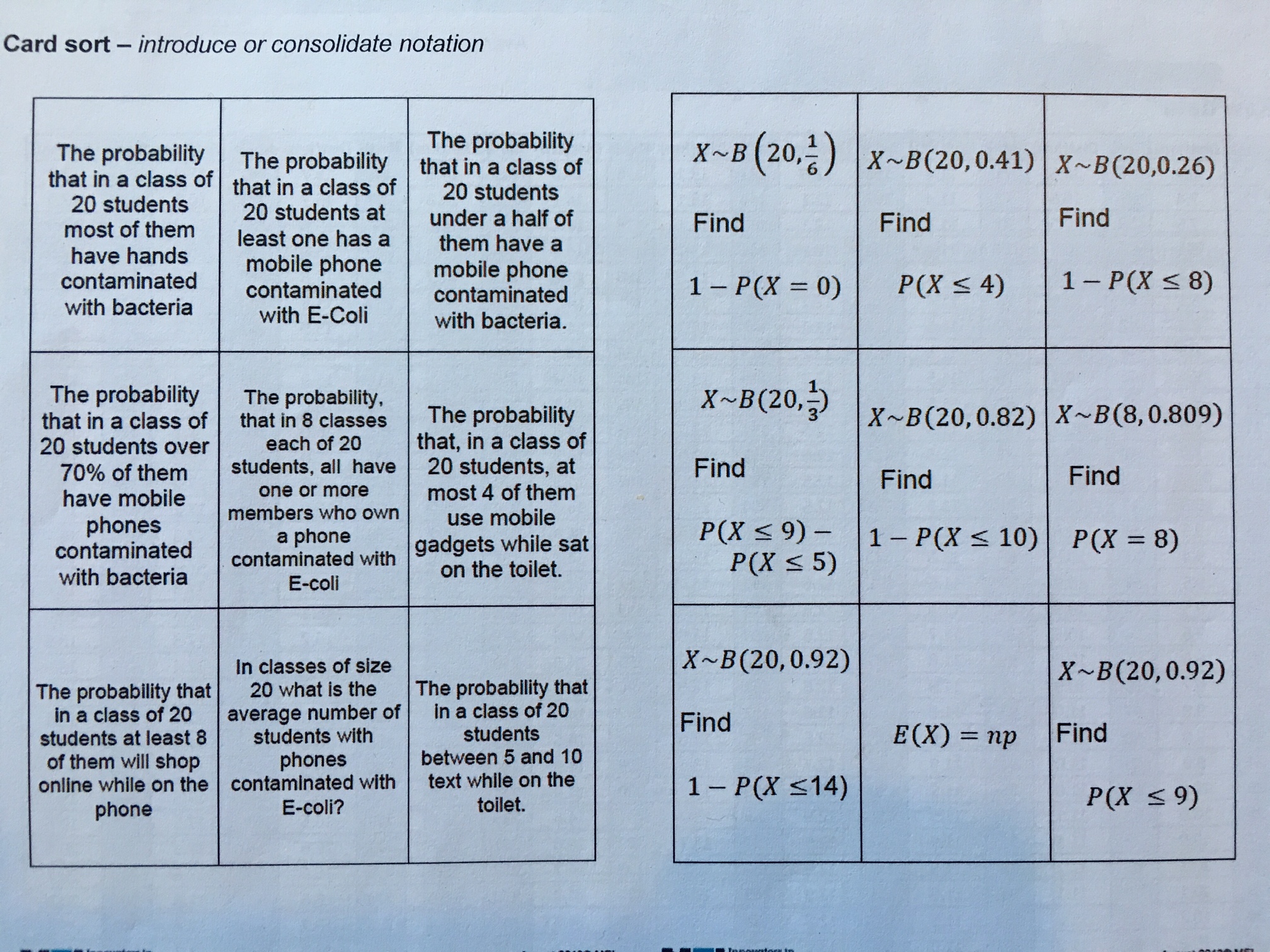
I think it is great that the card sort contains differing values of \(n\) and \(p\) taken from the information given.
Following looking at the Binomial distribution Terry talked about using data sets to obtain data that is approximately normally distributed. This is likely to be interesting in terms of the new A-Level, so I am going to do a bit of work on it and then blog at some point in the future.
Session 2 – Core Maths: a Teacher’s Perspective, David Phillip and Claire Phillips
At my school I am going to start teaching a Level 3 Core Maths next academic year and so I picked this workshop to get some ideas for classroom activities.
The initial activity of recording when popcorn pops in either a maker or a microwave was nice, but it’s hard to get accurate data due to issues with reaction times etc. Though, of course, this could lead on to nice discussions about the validity of recorded data.
I had a very interesting discussion with Mike Ollerton about whether some fermi style questions are more worthwhile than others. I am inclined to agree that students will get more out of some fermi style problems than others, but quite how to taxonomies this isn’t completely clear. Do you think some of the questions shown below are worth more (in a measure of learning) than others?
There were many other great resources shared during this session which will definitely be worth a look once MEI put all the materials up. I quite liked this matching activity: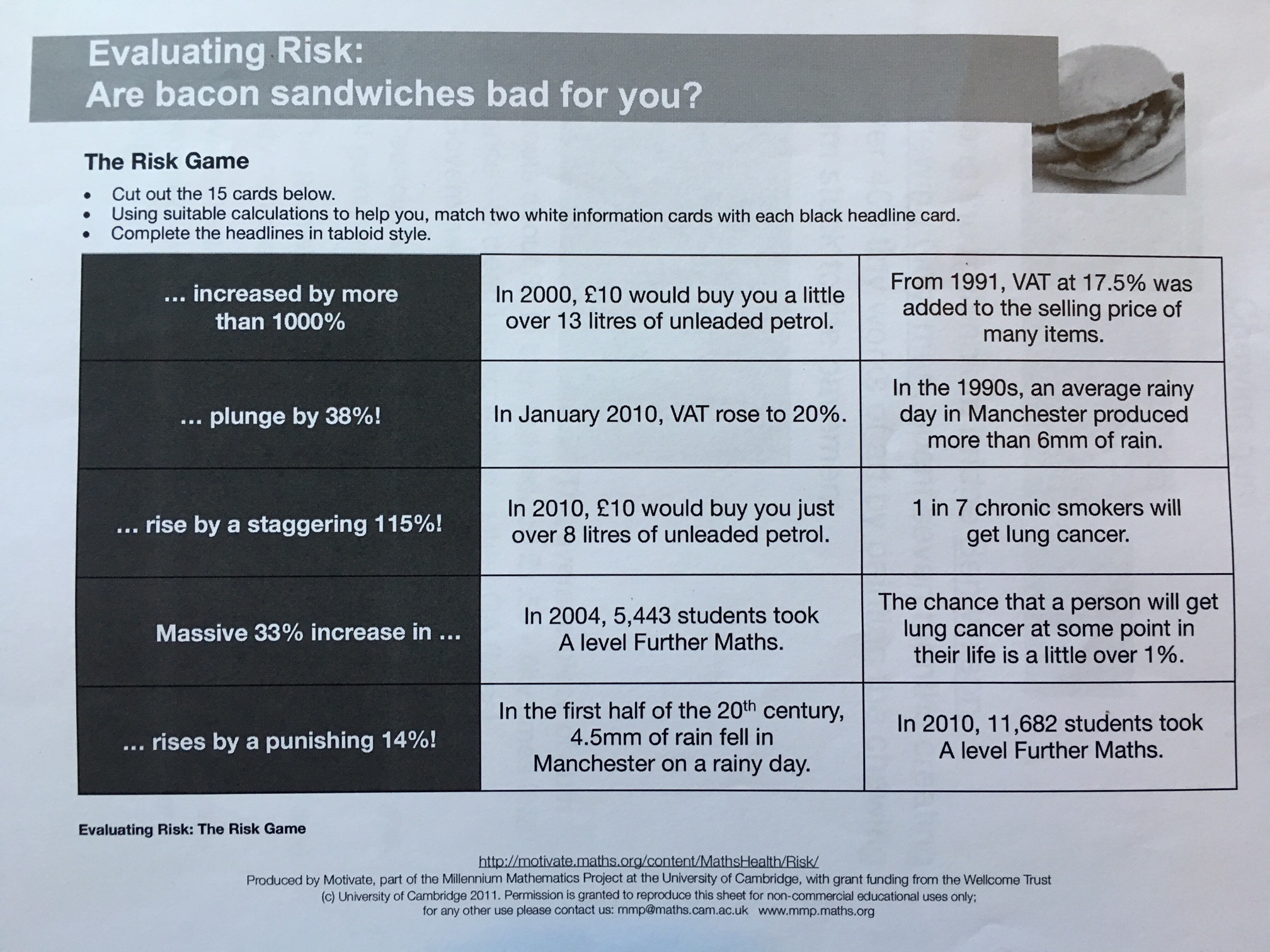
Session 3 – Teaching A-Level in Early Career, Cathy Smith
I found this session fascinating (as I do with Cathy Smith’s work in general) as in my experience there often isn’t much attention given to preparing ITE students to teach A-Level, and the demands of teaching A-Level are different to teaching lower school. I can definitely identify with some of these issues in A-Level teaching that were identified in Cathy’s research.

This quote from one of her study participants was particularly intriguing to me

I can definitely see where this come from, but I find it a little sad as if you do spend time on the preparation then you tend to get an awful lot out of the lessons.
As an added bonus from this session Cathy got all the attendees to work in groups on the card sort shown below.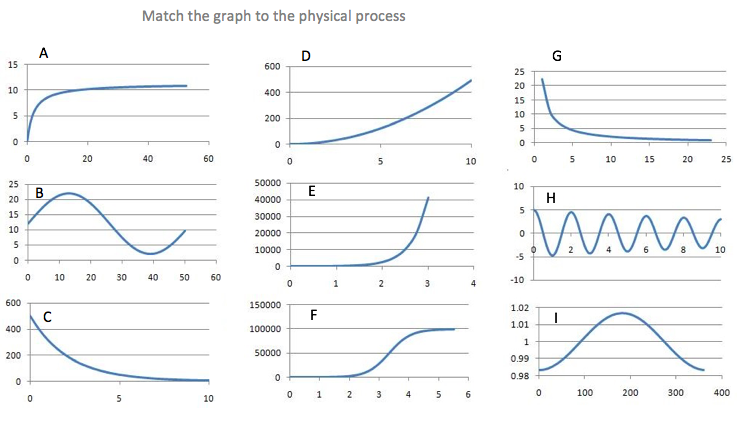
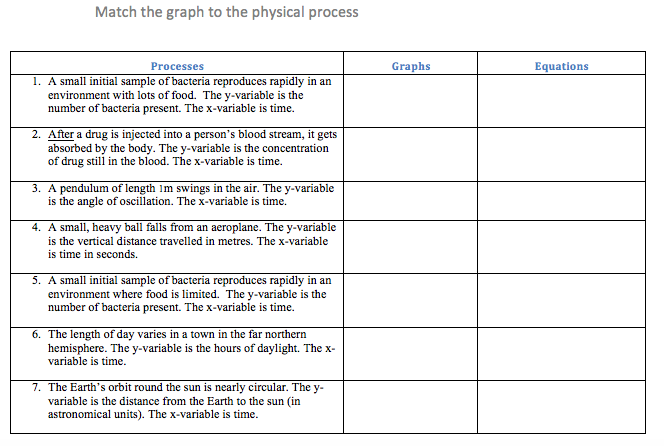
I really enjoyed doing this card sort and I think it would be a very valuable activity to do both with beginning teachers and A-Level students. Cathy made an interesting point about the language used in this task. She had re-written a task from nRich but been more consistent in the descriptions of the processes. For example each process starts with a description, followed by the \(y\) variable and then the \(x\) variable. This highlighted to me that getting the right amount of structure in an activity is very important. Too little is just as bad as too much! Interestingly, many people seem to start with the bacteria ones first, possibly for reasons of similarity.
Plenary – All Change in Post-16 Mathematics, Charlie Stripp
Charlie Stripp, the Chief Executive of MEI gave the first plenary of the conference. He gave a fairly positive talk about the state of mathematics education in the UK and the influences of all the changes coming through.
The picture of A-Level participation is very positive, though it remains to be seen how this will change in the future.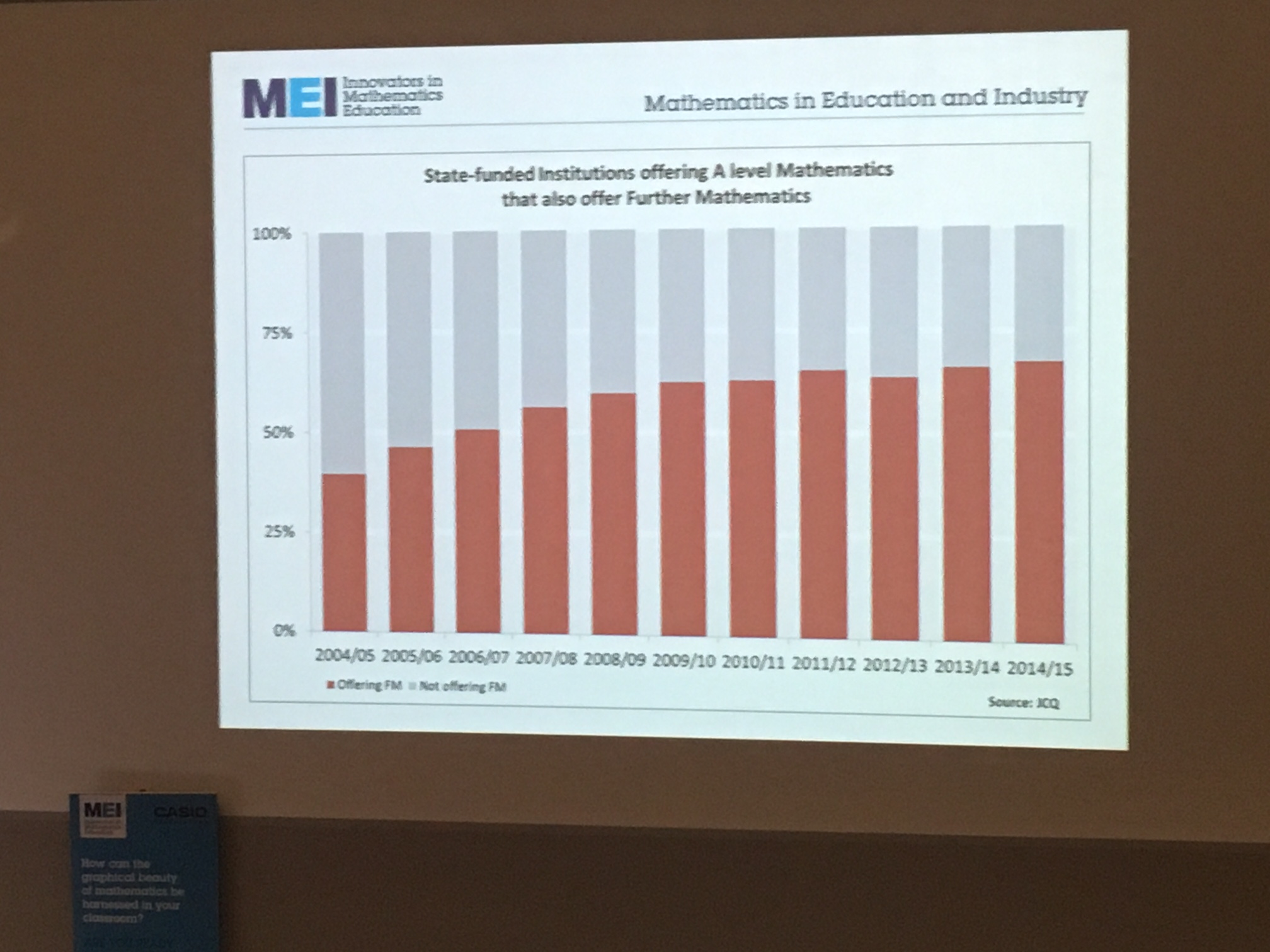
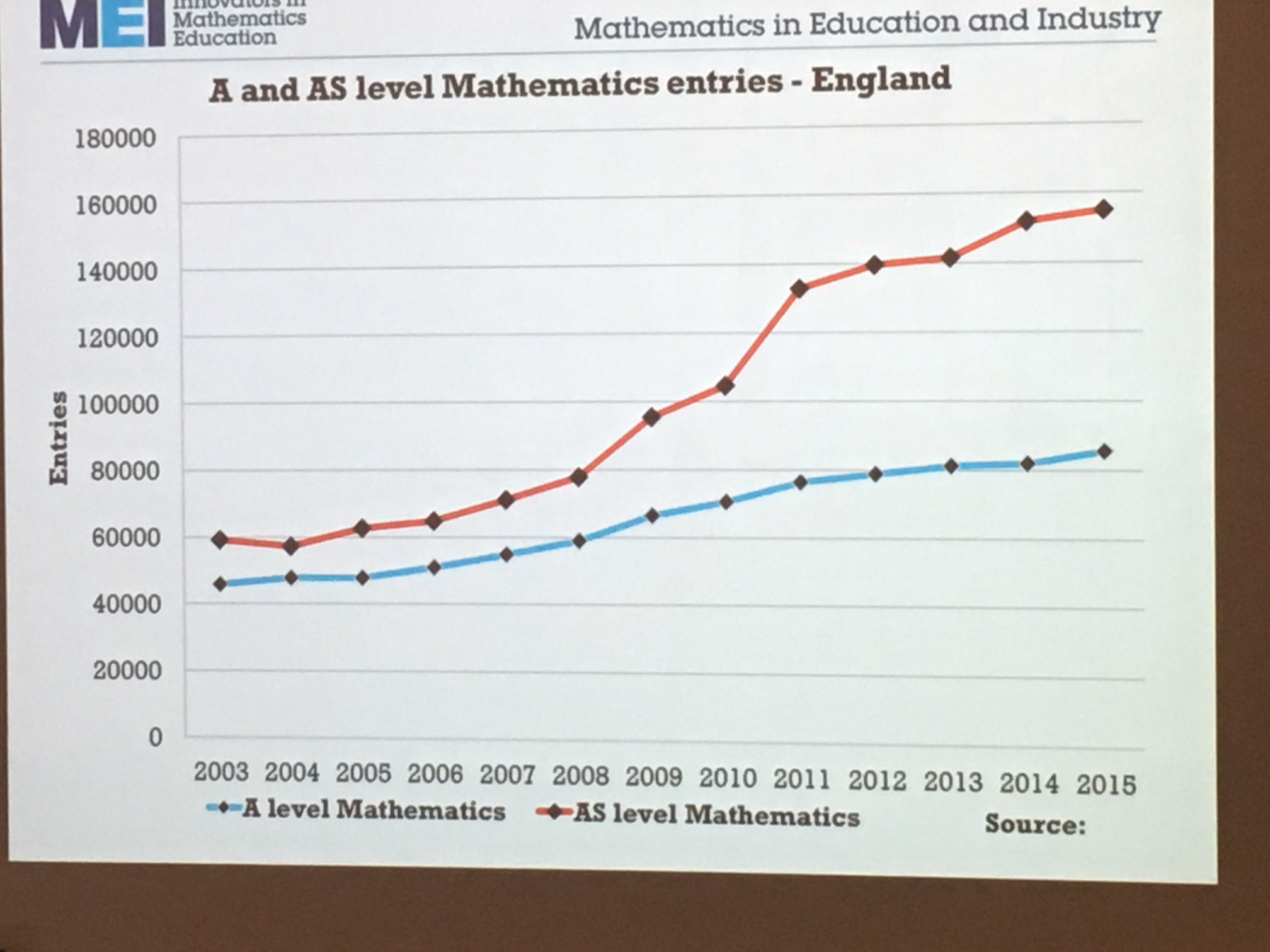
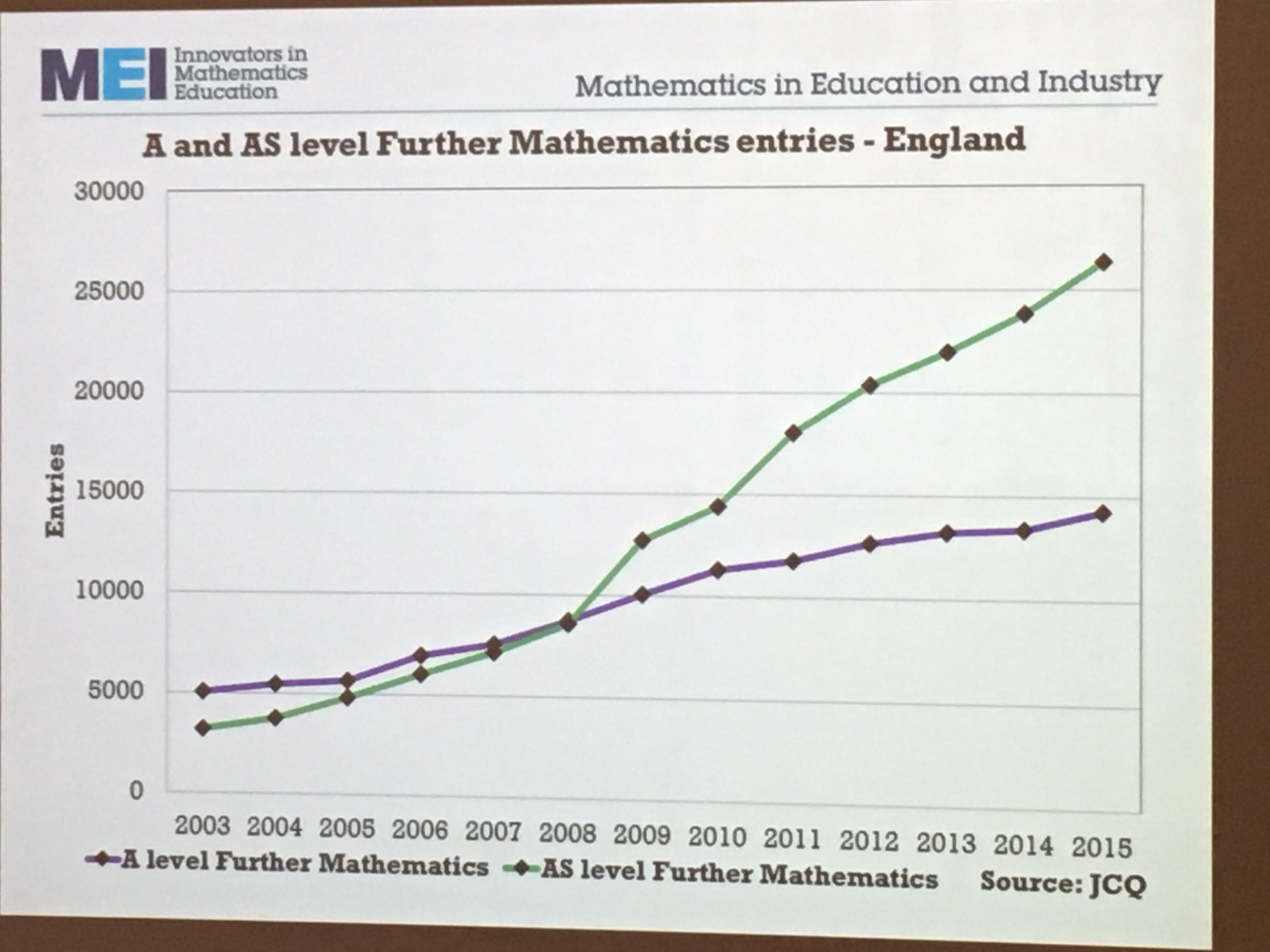
Charlie said that we have a “duty to use technology in teaching mathematics” and I completely agree with this. He also mentioned that there was research evidence that students owning their own graphical calculators helps their mathematics learning. I haven’t heard of this before, if anyone knows where this statement comes from please let me know!
Session 4 – Further Pure with Technology, Richard Lissaman
Being a keen programmer I was looking forward to this session with Richard Lissaman looking at the MEI unit Further Pure with Technology. A typical programming question from FPT is shown below

I think the idea of doing this kind of thing in A-Level as so much of real-life mathematics is computational, and I would love to do MEI maths so that I could do this unit.
I was quite impressed with the CAS capabilities of Geogebra. I’m not sure how robust it is, but for a free package Geogebra is very impressive.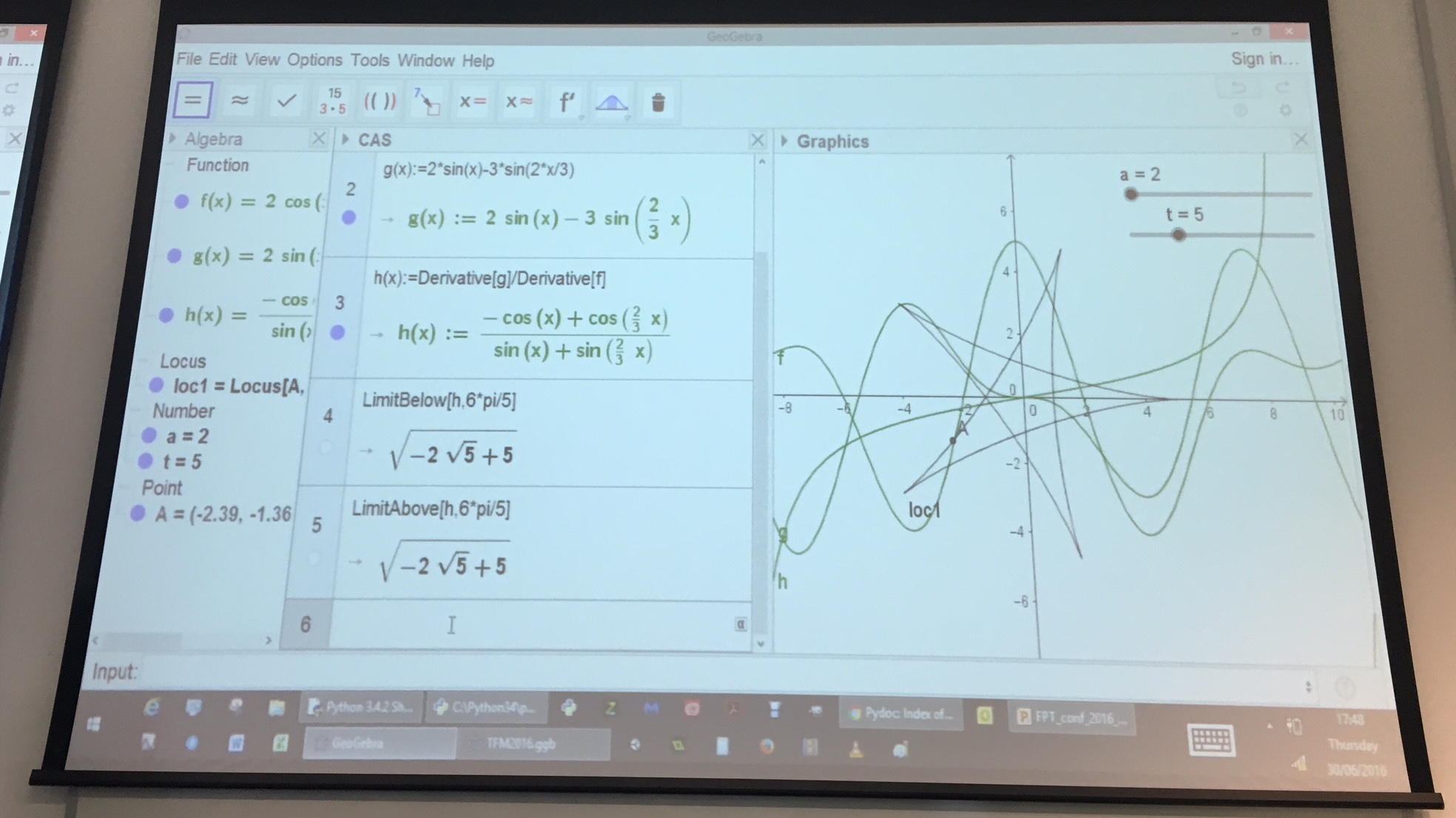
I’m glad that they have been able to incorporate FPT into the draft specifications for A-Level 2017. It doesn’t seem to have changed too much apart from replacing the complex variables section with content on differential equations.












