This book isn’t actually that old, it was first published in 1987, the edition I have is a reprint by Dover Publications.

For my PhD I studied the application of a particular class of finite element methods for the solution of the neutron transport equation. Finite element methods are a way to numerically solve a partial differential equation – maybe I’ll write more about this in the future. It works by discretising the domain into regions known as elements and then producing an approximate solution on each element. Importantly, these approximate solutions converge to the true solution as the mesh is refined and the elements become smaller.
In the field of finite elements, it is widely regarded as a classic, and is often the first thing that someone new to the area reads, indeed it was the first published book on finite elements that I read. This is due to the relaxed and easy to read style of the book.
There are the following 13 chapters:
- Introduction
- Introduction to FEM for elliptic problems
- Abstract Formulation of the finite element method for elliptic problems
- Some finite element spaces
- Approximation theory for FEM. Error estimates for elliptic problems
- Some applications to elliptic problems
- Direct methods for solving linear systems of equations
- Minimization algorithms. Iterative methods
- FEM for parabolic problems
- Hyperbolic problems
- Boundary element methods
- Mixed finite element methods
- Curved elements and numerical integration
- Some non-linear problems
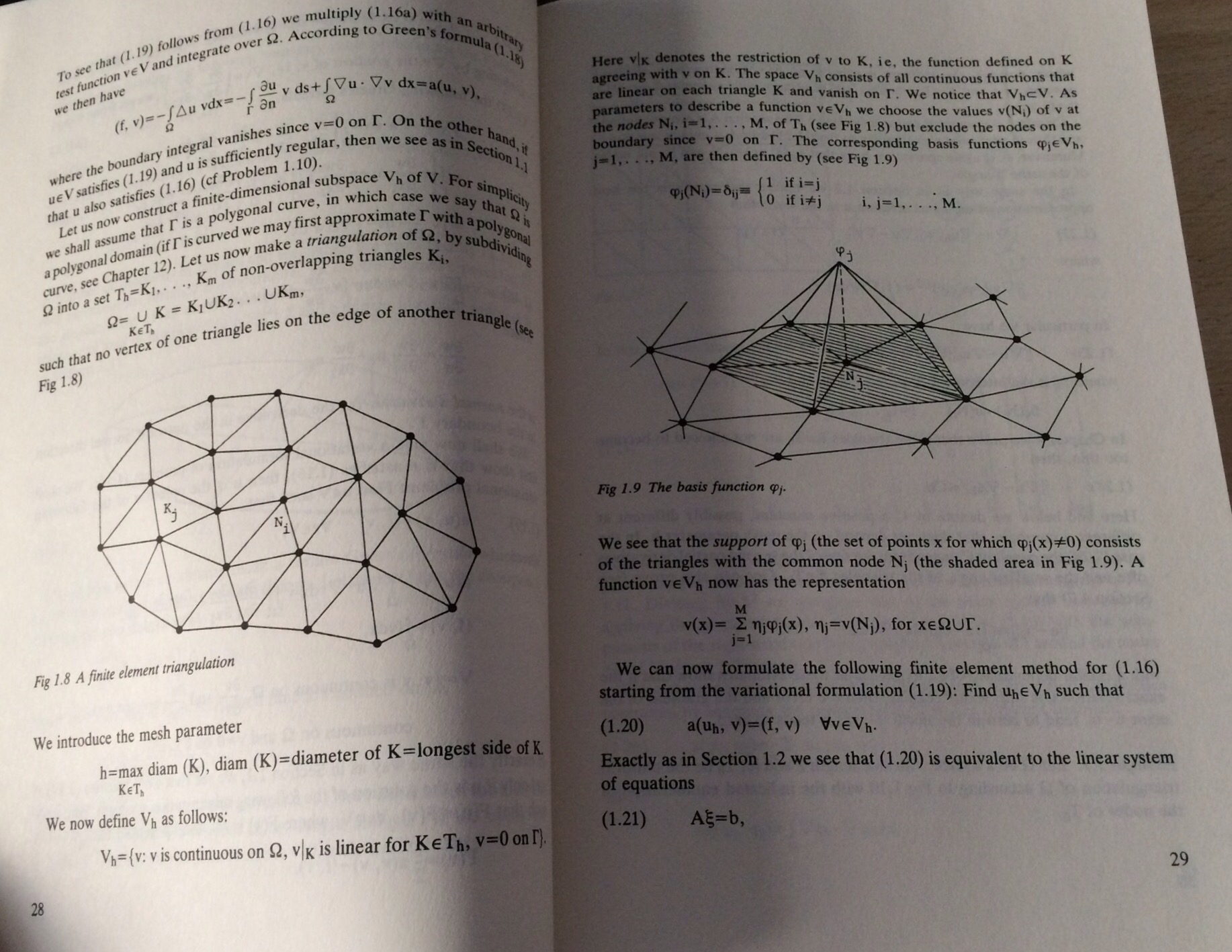
A really nice thing about this book is the mix of theoretical analysis and implementation details it provides. After reading this, you would be able to go away and code up a simple two dimensional finite element method. The book is well illustrated which helps with the understanding of concepts such as ‘basis functions’
As well as discussing finite elements the direct methods for solving linear systems is a fantastic introduction to this important area. The efficient solution of linear systems of equations is vital for any numerical solution of a real life problem that has been modelled by partial differential equations. This chapter serves as a great introduction to this topic (which will be considered more in future posts, and in a future classic books post). The chapters also contain a few stimulating questions, such as these from the linear systems chapter.

I think it is really nice that this book is written from a computational viewpoint (in addition to being mathematically rigorous) as after reading it, you can go away and code up the discretisation and a solver to try the methods out.
I would recommend this book to anyone who wants to learn about finite element method. The author did write an expanded book after this with some other authors, but it doesn’t read as nicely, and hasn’t generated the wave of good feeling in the finite element community as the original. In fact the sequel it is colloquially referred to as “The Black Death” (supposedly a term coined by one of the authors) as it is so bad!!