I’ve been pretty slow writing about this but on Wednesday 11th March Mathshubs East Midlands West held this half term’s Secondary Curriculum Development Meeting.
Aswell as being a chance to have a few cakes (I particularly like the granola bars topped with strawberry jam and seeds) Matilde Warden (@jordanvorderman), the maths lead for the East Midlands West Maths Hubs discussed improving reasoning in lessons.
She started by highlighting aspecs of the new national curriculum concerning mathematical reasoning and problem solving before we looked at a couple of problems from the nRich website, specifically the Stage 2 problem Fitted and the Stage 4 problem Steel Cables. The nice thing about these is that the nRich website (along with all the others in this collection) is that they show a few approaches to the problem that some students have tried. I had seen the Steel Cables problem before, but had never really considered different approaches before – the default to me was to find the quadratic nth term rule to predict all the terms.
We also briefly looked at an article by Malcolm Swan, also available on the nRich website here. In the past, when doing problem solving lessons I confess that I normally spent only one lesson on them, and valued the thinking during the lesson and the verbalising of mathematics that happened with this. However I probably didn’t build on this terribly well to develop pupil’s problem solving approaches and build resilience.
In the article, Malcolm suggested a two lesson approach where for the first lesson pupils work individually on a problem without help. At the end of the lesson you collect in the work and look through them (but don’t formally mark them!) so that you have an idea of how to move their thinking forward. Then, in the second lesson allow pupils to work in pairs to share their thinking, prompting them if necessary to move thier thinking forward.
I decided to try this approach with one of my Year 8 classes and chose to look at the Steel cables problem – we had done quadratic sequences before Christmas so was interested to see if anyone would go along those lines. A couple of pictures of pupils work are below (the first is at the end of the second lesson, and the second piece isfrom a different student at the end of the first lesson)
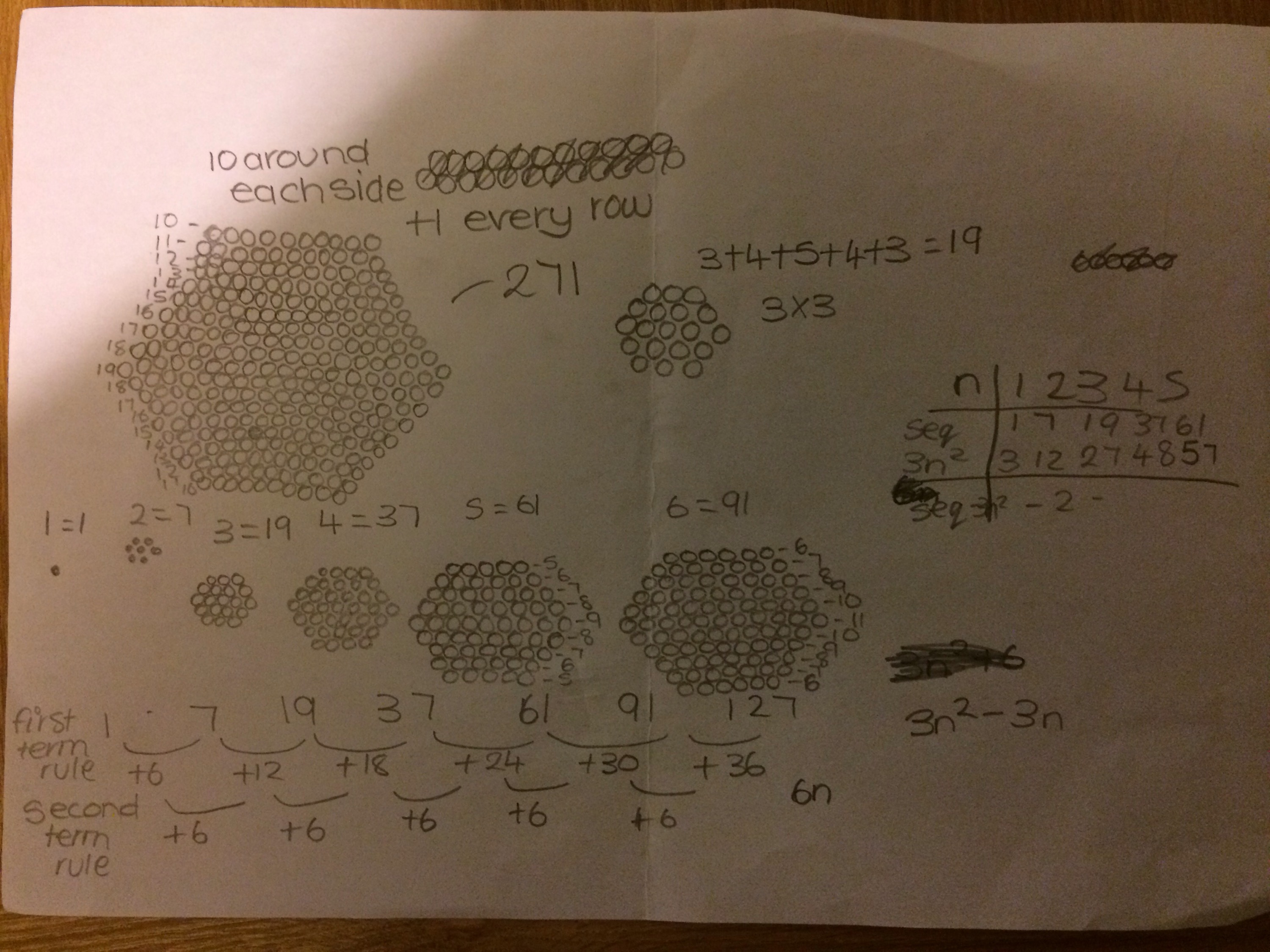
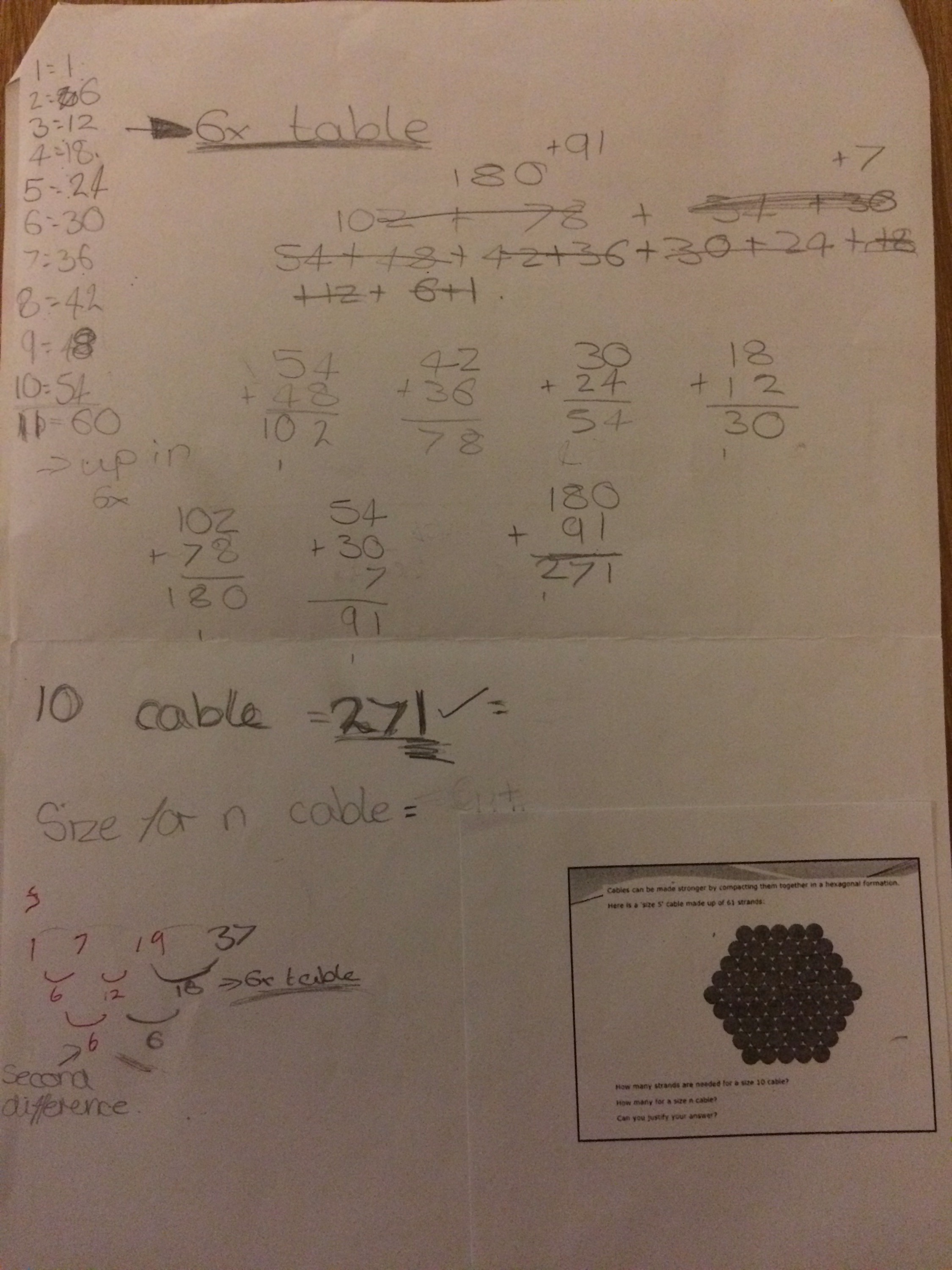
Lots of different approaches were used, though drawing them out and counting methodically was a dominant approach. However the second picture shows the first person to answer the “how many strands in a size 10 cable” question, and she noticed that by counting in rings outward each new ring contained 6 more strands than the previous ring, and used this to work out the number of strands for a size 10 cable, before spotting that the pattern was related to the 6 times table. I also saw pupils spot the vertical symmetry of the cable and split the cable up into large and smaller triangles. Strangely though I didn’t see anyone split it up into quadrilaterals like one of the sample pieces of work on the nRich website.
Malcolm also suggests showing sample work to pupils and getting them to critique it, and develop it further. Unfortunatey I didn’t have time to do this, though this is something I intend to do in the future.
He ends his article by suggesting that teachers let pupils see their reasoning and tackle a problem unseen oon the board. This is something I try to do every lesson with my sixth formers. I enjoy tackling a question that I haven’t though about before, I think it is important for pupils to see me struggle with arithmetic sometimes and try iincorrect approaches and double back on myself. After all, making mistakes is really what maths is about.