After having to set my alarm for 04:30 in the morning to make the train I needed to get into London and enduring an annoying rail replacement bus I’m glad to say that #mathsconf4 was fantastic; as the previous ones have been!
Before I describe in a bit more detail I want to mention the only negative aspect – no breakfast pastries. If you know me you will know that I get strangely excited about that kind of thing, so this was very sad. The cute little pot of jam that was given to me by (@tessmaths) did make me very happy though.
I’ll try to briefly describe the best bits of the sessions I went to, and leave the detail to the people who them!
Speed Dating
The day started with speed-dating to swap activities. In the past I haven’t been great at this, and always wish I had recorded what I had spoken to people about more. So this time I was more planned (I shared my Further Pure 1 geogebra conics task which I have described here) and wrote down the great things I was told about:
Dawn Denyer (@mrsdenyer) shared her worksheet for low attaining groups which has the answers for each question somewhere in a grid for them to find and know they have likely done it correct. I’m going to try this with some of my classes.
Deb Friis (@runningstitch) talked about the idea of using the “boxing up” technique to get students to write number stories, structured like they would write a story in English. I have seen this technique before from @HelenHindle1 of Growthmindsetmaths.com, but I really liked seeing how it could be used in conjunction with a problem solving lesson to structure pupils thinking without guiding them on what to do.
Japleen Kaur (@japleen_kaur1) talked about using the date as a starter similar to the Commonly known Four Fours problem. I think this is a great starter if you are moving rooms and need something simple students can do whilst the computer loads etc as it reinforces key skills. If as Japleen does it is done regularly it could become a good habit to ensure maths is happening straight way. I liked how even her Sixth form class found this useful.
For the last person I spoke to someone I wasn’t already following on Twitter; Jen Chan (@JenJenDes) showed me a learning grid for area and perimeter. I keep meaning to try these after I had been shown one in my school by an English teacher, so it was good to see an example of a maths one!
Mark McCourt
Mark delivered the keynote this time round, and it was nice to have a change from the last two, especially as Mark is always an entertaining speaker. He was speaking on the subject of “How can we improve Mathematics Education for all”. His starting point was the fairly depressing assertion which is – we can’t. He discussed Japan, which is seen as a high achieving nation but still reflects on their maths education system and wants to find ways to improve it. He showed this quote from Japan:
“[If in Japan], the aim of mathematics education is to make pupils hate mathematics, then in this point we may have succeeded”
He also used another quote that I like to refer to from a paper by Jeremy Hodgen (@JeremyHodgen), who is now at the University of Nottingham and co-authors:
“For every aspect of mathematics education linked to high performance in one country, a contradiction can often be found elsewhere'”
This quote led nicely into Mark’s main point – the importance of culture. All the High performing Shanghai countries have a very different culture to ours and this has a massive impact – what works in one place may not necessarily work elsewhere. I was really interested to hear about the paper where the high performance of western born children of East Asian descent was investigated. Tim Stirrup ( @TimStirrup) kindly supplied a link to the paper and I will definitely be reading this during the next week or so.
Mark ended by saying that something that teachers can do to improve maths education is for them to be “intelligent, independent and not just tow the line”. I whole heartedly agree with this.
Now onto the workshops!
From Euclid to You
Emma Bell (@El_Timbre) delivered an excellent session looking at some books in her impressive collection of old maths books. She has uploaded a padlet containing her source materials here.
The mention of Euclid’s elements led to an interesting discussion about Euclid’s five postulates and which ones are used when answering a variety of geometry problems from across the key stages. Maybe we should bring more history into our lessons? I know I don’t mention the postulates in a regular lesson on shape!
Emma also shared a great problem concerning birds from Leonardo of Pisa’s (Fibonacci) book “LiberAbaci” from 1202. I think I may write a separate post about this as it is a good introduction to under-determined systems…
There was a lovely quote from a 1958 book where Bodmas was described as a “travesty of mathematics”. I liked this whole page of division questions phrased in different ways

And I thought the way this question concerning the days between different months of the year was particularly nice:

I recommend that you take a look at Emma’s padlet where the presentation can be downloaded with some of the source materials. Emma has also shared an essay she wrote during her PGCE on proof – I’ll try to have a read of this at some point. Thinking I should also share a 6 lesson plan I wrote on circle theorems during my ITT – I’ve not looked at it since!!
The Best of the U.S.
This session was delivered by Craig Jeavons (@craigos87) who talkedabout some things from the States. Maths educators from the U.S. are very active on Twitter and maintain a directory of members of the MtBOS community here. Craig explained that he liked using stuff from the States as they are culturally similar to us and their Common Core State Standards (pretty controversial over there) are actually quite similar to our new curriculum.
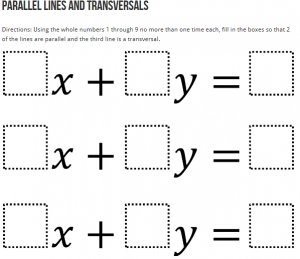
I’ve used the websites estimation180.com and grapthingstories.com before. I find graphingstories really good when working on real life graphs, with all ability ranges – some of them are actually pretty tricky. The fact that the website is american also provides a good excuse to look at imperial measurements. I’ve only recently come across the website openmiddle.com, and am curently putting some of their questions into my school’s new Year 7 mastery curriculum. As the name suggests, each question has the same start and end point but there are multiple ways to get to the solution (i.e. an open middle). The website is really useful as it categorises the questions by their Grade (remember that a US grade 6 is the same as an English Year 7), and goes up to the end of high school. I really like this question:
 Craig then talked about Robert Kaplinsky’s Depth of Knowledge (DOK) charts, for example the one below which I hadn’t seen before
Craig then talked about Robert Kaplinsky’s Depth of Knowledge (DOK) charts, for example the one below which I hadn’t seen before 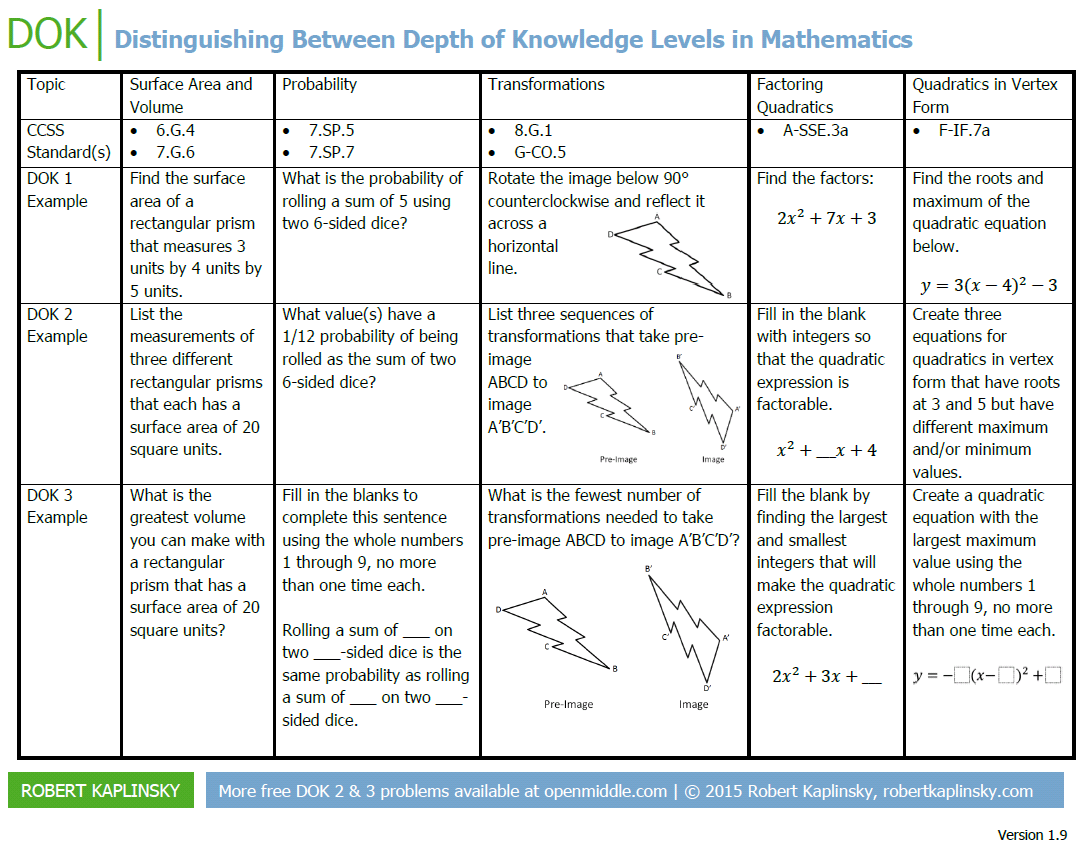
I’d heard of the DOK as an alternative to Bloom’s Taxonomy (I’ve always been pretty derisory of Blooms to be honest!) before but I hadn’t seen it applied to maths topics before – very interesting and lots of questions OpenMiddle questions in the grid too. I think it would be nice to have something similar for all topics really.
I’m also grateful for Craig pointing out the curriculum maps on emergentmath.com. These link to the Common Core Standards and contain some links to great activities, such as this one “Square Roots go Rational” from NCTM. I’ve bookmarked these for a proper explore during the summer holiday.
Tweet Up
After a great cooked lunch (thanks LaSalle, the lamb stew was really good!) it was time for the tweet up. I played a very minor part in helping run this, all organised by the wonderful Julia Smith (@tessmaths) and with Dawn Denyer (@mrsdenyer) providing us all with some great T-shirts. 
From Left to Right: Dawn Denyer, Nicke Jones, Julia Smith, Emma Bell, Martin Noon, Danielle Bartram, Jo Morgan and me.
We had lots going on, including Jo’s lowest integer game, the QR Cubed Cube, a photo booth, some lovely O-Level questions. Make sure you come along to the Tweet Up at the next conference everyone had fun – here’s Beth (@MissBLilley) with her folded cube:

What I Learned from Teaching new GCSE content to Year 10 and 11 Students
This session was delivered by Sarah Flynn, a head of department who is also a maths advocate for AQA and as such helps schools in delivering AQA content. I was hoping that there would be more discussion on ways to teach some of the new content, but it was definitely good to look at some questions on topics (mainly graphs and Venn diagrams) that are going to be in the new syllabus and see exam questions from the Linked Pair Pilot programme. We discussed the following question:
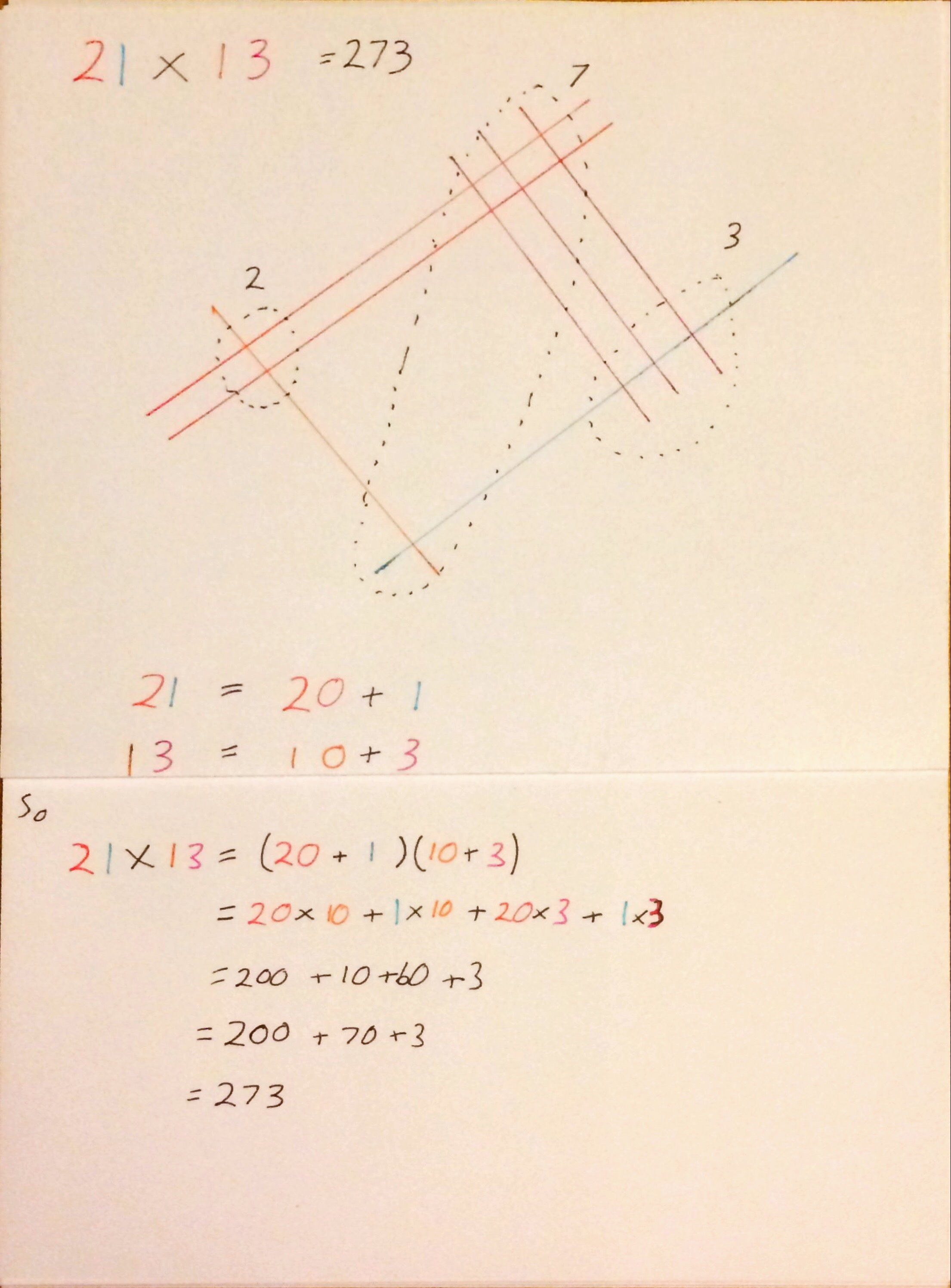
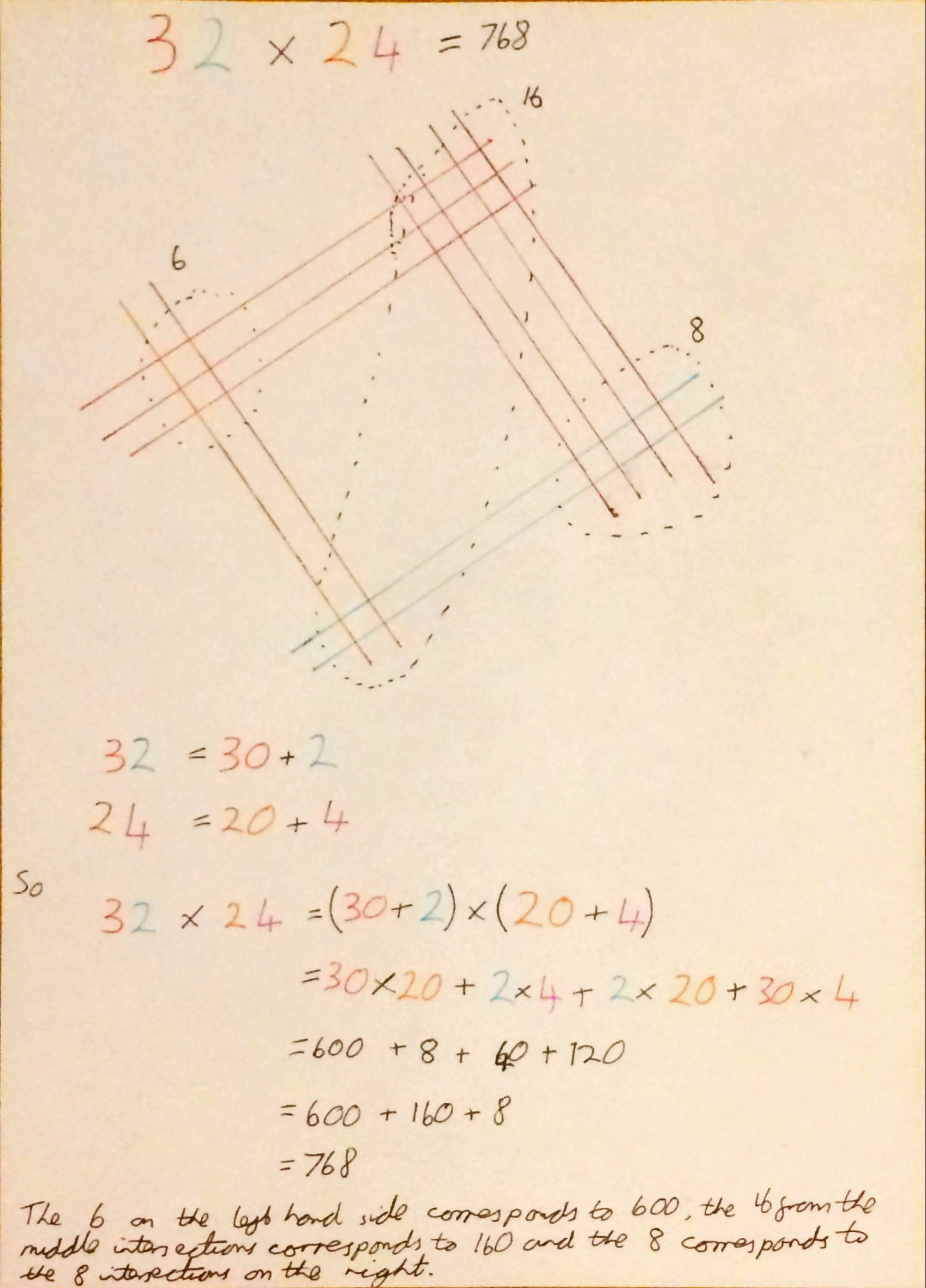
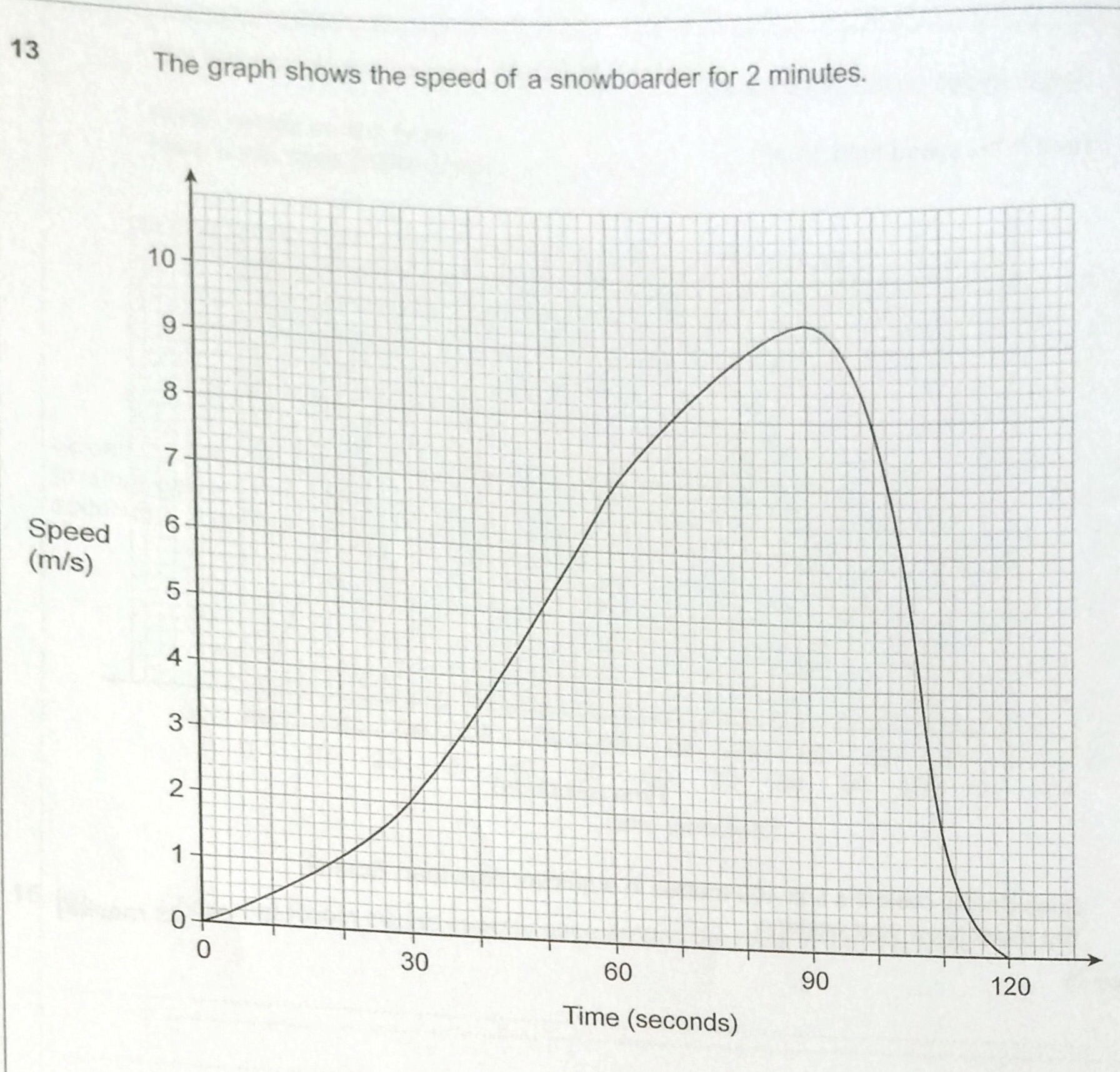 The question asks you to estimate the distance travelled by the snowboarder and state the units of the answer. I was surprised to learn from Sarah that the mark scheme said that the graph should be approximated by 5 shapes – seems like overkill to me! I need to go away and look at the mark schemes for these kind of questions before teaching to get an idea of the error bounds and what is expected. During this session @MissNorledge showed me this trick for finding the exact trigonometric ratios for 0,30,45,60 and 90 degrees.
The question asks you to estimate the distance travelled by the snowboarder and state the units of the answer. I was surprised to learn from Sarah that the mark scheme said that the graph should be approximated by 5 shapes – seems like overkill to me! I need to go away and look at the mark schemes for these kind of questions before teaching to get an idea of the error bounds and what is expected. During this session @MissNorledge showed me this trick for finding the exact trigonometric ratios for 0,30,45,60 and 90 degrees. 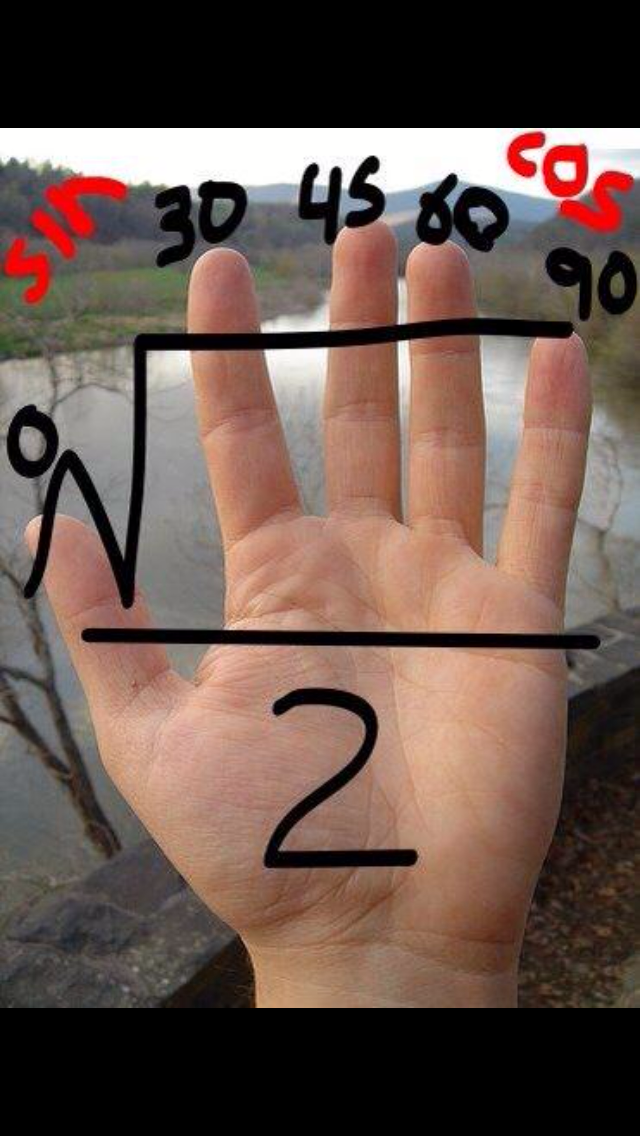
I hadn’t seen this before, and generally aren’t keen on tricks – I’d obviously prefer for students to just learn them or be able to derive them, but I do think this is pretty neat!
For me the take home message from Sarah’s session is to not underestimate the students. They may be able to do some of the questions that we feel are more challenging even if they don’t manage the more “basic” questions.
The past papers from the Linked Pair Pilot are worth checking out, there are some quite nice questions, such as this one from 2014: 
These questions do generally seem less challenging than the questions in the new specimen papers though!
The Art of Leading a Mathematics Department
I was really looking forward to this session by Amir Arezoo (@workedgechaos) and it definitely didn’t disappoint! I decided to go this one as leading a mathematics department is something I aspire to, and I thought it was worth getting some tips early 🙂 I was annoyed though that this session was blocked against Martin Noon’s (@letsgetmathing) session about marking – luckily he tweeted out a link.
Anyway, back to Amir’s session (which I like to think was enhanced by the use of my clicker haha). I loved how he used his wife’s description of him to start the session – “daddy, mathematician, geek and moody” – thought it was really useful that he had split the talk into the following 11 key questions to ask yourself as you take over a department
- Is your department serving the needs of its students?
- What is your vision for your students and your staff?
- Do your staff currently have the capability to meet these needs?
- How do you determine what is best for your students and staff?
- What does your curriculum look like?
- How do you engage your students?
- Do you and your staff reflect on practice?
- How do you know that you’re moving in the right direction?
- Who do you look to for guidance?
- Why did you become a leader?
- How do you grow the essentials?
Using a set of questions to frame the talk seemed to really help me to reflect on my views as the session progressed and after.
Amir emphasised that he didn’t believe that recounting what worked for him was useful as what works in one department wouldn’t work in another. This led to a nice tie in with Mark McCourt’s point that context is important – the context of the department within the school / within the community is important. How the community views the importance of mathematics is going to affect how your pupils view mathematics and what your student’s needs are. I was very interested in his mention of a “common calculation policy” and looking at my notes has reminded me to ask him more about this! His retort that “Bodmas is a waste of Oxygen” led to a bit of a discussion between a few of us about why we don’t like Bodmas on Twitter which was good.
Amir shared his experiences of things which didn’t work for him, such as trying to change everything in a department in one go.
When talking about point 5 he referenced the great picture from William Emeny of Great Maths Teaching Ideas shown below
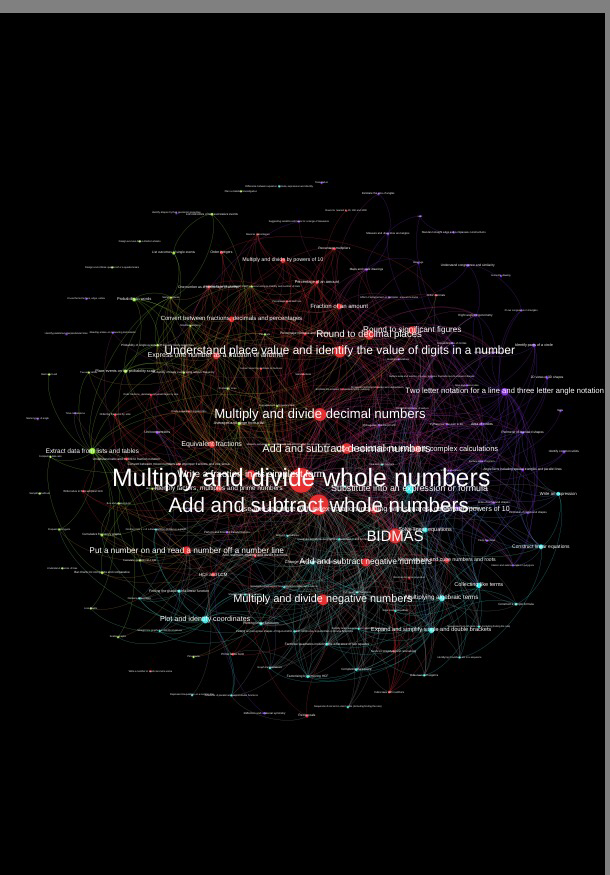
The high resolution image is available here. I love this network so much that I have it on display in my classroom. As Amir says, it is important that any curriculum addresses the topics that have the highest weight in this network. He talked about having an open door policy – I really like this idea, and I try to ask for feedback from any other teacher that walks into my lesson.
There really is too much good stuff from this session to write about here – Amir please can you blog about it yourself?
To sum up the main points of the session I will use the same quote that Amir used “Character succeeds where personality only promises” – the human side of leadership is important!!
Other Stuff
Meeting more people who i have spoken to on Twitter in real life was great, and I had some fantastic discussions in the pub afterwards; both with people I have met before and those I met for the first time at mathsconf4. There are too many people to mention here…
I’m also sure I have forgotten many great things from the day too.
It was another fantastic event organised by LaSalle and I can’t wait for the next one.