Whilst I was out tutoring last night I missed a post from Jo (@mathsjem ) about Prisms… There was a debate about whether a cylinder was a prism.
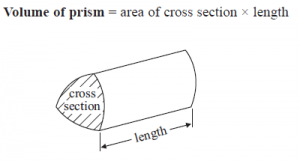
I had always understood a requirment of a solid being a prism was that the base of a prism was polygonal – i.e. made up of straight lines. This means that a cylinder cannot be a prism. However, the formulae sheets from GCSE papers seem to disagree, as this picture from the Edexcel papers shows:
Here we have a “prism” that clearly has curved edges forming the cross section.
I know quite often the volume of a cylinder is taught by referring to it as a prism with a circular cross section, but I haven’t seen any reliable definitions of prism that include cross sections with curved boundary. Instead, all definitions I have seen specifically require that the face is polygonal, for instance this definition from Wolfram’s Mathworld. Here they reference an old book on solid geometry as a source of this definition – Solid Mensuration with Proofs by Kern & Bland – @El_Timbre do you have a copy of this by any chance?
Keith (@MrKMorrison ) suggested that the word prism comes from the greek ‘prisma’ which literally means ‘something sawed’, suggesting the same face throughout, and so a cylinder should be a prism. I think the root of the word is largely immaterial, once an accepted definition is present. For instance multiply is a word in general usage and with a precise mathematical meaning, the root of multiply is the old French (I believe) for increase, but mathematically we wouldn’t use the word multiply to mean this.
In the grand scheme of things I guess it isn’t really a big deal to call a cylinder a prism – a cylinder certainly “behaves” like a prism, and maybe for lower attaining students calling a cylinder a special prism perhaps helps. For students going on to study maths though I think being loose with definitions can lead to problems, especially once they get to university.
I alluded to prime numbers in a tweet this morning as being what I think is the most dangerous example of miss-teaching of definitions / miss understanding of a definition. I’ve had so many students (including undergraduates) say to me that 1 is prime because it only has 1 and itself as factors. This is despite the definition of a prime number explicitly excluding 1. I’ve always found this quite odd……
Update: Mike Lawler (@mikeandallie) provides me a link to this nice definition from the Art of Problem Solving