After a quick McDonald’s breakfast treat (the Suasage and Bacon sandwich is back!) I begun the early drive down to Peterborough for #mathsconf6. It was a fantastic day, and it was lovely to catch up with many friends again and meet. This post aims to provide a bit of a summary of the day… This time I have tried something new and wrote bits of this during the day (and then fleshed it out later) instead of writing lots of notes and then typing up a post. It has turned into a bit of a mammoth post!
The Opening Address – Mark McCourt – La Salle
As always an amusing introduction to the event where he made the point that between Year 1 and Year 11 there are only 320 mathematical concepts that students need to master and they have to do this in around 1600 hours of maths teaching. I have to agree with him – surely we should be expecting everyone to manage this?! However, for some reason this currently doesn’t happen.
Andrew Taylor – AQA
Andrew started by sharing a few of the things he hates about assessment (this isn’t all of them, I was stupidly distracted making some last minute presentation changes):
- Getting the grade is in the way of students getting a deep understanding of maths. “Surely we can find a way to get above that”.
- Testing for the sake of putting numbers on a spreadsheet.
I really liked how he expressed a desire that kids grow up with a love of maths and that they appreciate the power of maths.
This speech I found really interesting as it wasn’t a conventional exams and assessment update; it was a much more personal view of what he values in education and assessment. He mentioned the Cockroft Report as a a large influence on him, and I was interested to hear that Cockroft had expressed a concern about students taking exams where they can only achieve a third of the marks – this is certainly still an issue today. The SMP books also got a mention – I wish these books were still being published 🙁 Andrew emphasised that the most important key to success is “to go back to great teaching” and it is this that will get good results. The issue of jumping around tiers to obtain extra marks by “gaming” the system, for example, is going to be a lot harder to do with the new GCSEs and so we need good teaching to ensure everyone achieves.
A great quote from Cockroft is the one shown below on testing:
 Andrew then talked about what AQA does to help, giving the three points below.
Andrew then talked about what AQA does to help, giving the three points below.
- To get the correct assessment you must have the curriculum expertise; and this is why they have an expert panel meeting of people involved in maths teaching and maths education.
- Listening to people who use AQA and responding to provide the information that they require.
- They work hard to gain the trust of people using the assessments and providing the results. AQA strive for consistency in the questions / papers they produce.
Speed Dating Segment:
Despite best laid plans I hadn’t got my thing to share and instead I talked about the upcoming KS5 CPD day I’m organising in August. I managed to pick up some great ideas from others though, which I have summarised below.
Megan Guinan – Megan first shared the Tarquin protractors; I’ve not seen these before and it is cool that they are flexible.
 She then talked about how to fold a Kite out of A4 paper and shared some excellent pictures of display work produced by her students. The link she shared for instructions for this is very good.
She then talked about how to fold a Kite out of A4 paper and shared some excellent pictures of display work produced by her students. The link she shared for instructions for this is very good.
Deb Friis – Shared the MEI Introducing Trigonometry material – I particularly like the Aqua Ferris wheel idea for plotting sin graphs above and below the \(\) x-\(\) axis.

Jennifer Shepherd – I really really liked this idea for a constantly changing display that Jennifer shared
 It shows a progression of a topic through the Key Stages really well, and nicely allows students to contribute to a display that is easily kept fresh. Since the event Jennifer has tweeted a picture of her display,which I have included below.
It shows a progression of a topic through the Key Stages really well, and nicely allows students to contribute to a display that is easily kept fresh. Since the event Jennifer has tweeted a picture of her display,which I have included below.
 Emma Brooksbank – Quick and easy marking: At then end of every lesson she puts a question on the board which students answer on a post-it note which she then collects, marks and returns. The idea of returning the post-it notes is simple but something I don’t think I have ever done.
Emma Brooksbank – Quick and easy marking: At then end of every lesson she puts a question on the board which students answer on a post-it note which she then collects, marks and returns. The idea of returning the post-it notes is simple but something I don’t think I have ever done.
Philippa Winstanley – Problem of the Week: All year 10s do this to develop their problem solving skills. She shared a lovely bookmark of problem solving strategies that she gives each pair. I wish I had taken a photo of this…
Following the sped dating it was on to the workshops.
Workshop 1 – How to Get The Most From Your Data
As I am a massive data geek I was really looking forward to Amir (@workedgechaos) and Ben’s (@MrBenWard) session
In answer to the question “What is data?” They provided the following 3 points (I particularly like the third one), before saying that it is not a panacea to all your problems and in fact often creates more questions than answer.
- The result of recording the results and attainment of students.
- A source of information to inform decisions about your department.
- A means of providing objectivity around often subjective arguments.
Ben made a very good point that we should be “measuring what we value” and not just creating value in “what we measure”. This post by Tom Sherrington (@headguruteacher) about the following diagram is well worth a read and I am thankful for them highlighting this as I had missed it on Twitter.
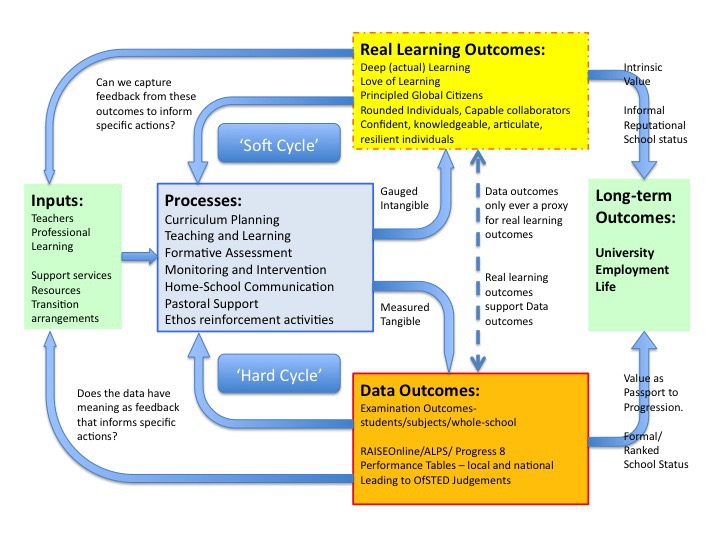
Most maths teachers I am sure see themselves as being pretty data savvy but Amir talked about the fact that being data savvy isn’t just about collecting data it is about using it effectively. I really liked how they included the concept of “live data” being used in the classroom such as QuickKey, diagnostic questions etc which can be used to inform (and modify) classroom teaching instantly. I’m guilty of not including this in what I see as data, and to be honest I don’t know why. I should make more use of this kind of data, and I actually think that recording this data could give me some interesting insights over a longer time frame of say a few years – definitely something for me to consider…..
The use of a spreadsheet containing information about staff interested me as I think many teachers would find this controversial and be reluctant to have this used in a department. I feel that as long as this was used in a non-judgemental way (which Amir emphasised that it should be) it could be really powerful in terms of quality assuring opinions on colleagues, identifying each teacher’s strengths that could be shared with the department as part of some CPD and identifying any support that is needed to ensure a department of all staff are happy. Ultimately, I believe that being happy in the workplace has a large impact on performance (both of teachers and of their students) and using data can help to ensure happiness.
I also thought Ben’s comment about having a department meeting to complete data entry together was fantastic as this would definitely open up the department in terms of sharing their planning and assessment of students. The importance of teachers valuing their data I think is also key: if staff value their data then it is more likely to have an impact on their teaching and change aspects of their teaching. From a personal point of view, at the moment it is easy to not value the data that we are entering for our Year 10s, for example, as we don’t have much knowledge of how the new GCSE is graded. However, we should keep in mind that across the year cohort this data is still powerful.
I am a big fan of data, but it is certainly important to remember that the data cannot tell the whole story as every pupil is an individual and so the use of data needs to be supplemented with professional judgement and knowledge of the pupils which can only come with devoting time to get to know them. But, being devils advocate here – could we just not collect more data?! (I think I may write more about this over the coming weeks once my thoughts have crystallised a bit).
Over the next few weeks I will certainly be thinking about and reflecting on these 3 questions:
- What do you need your data to do in your context?
- What gaps do you need to fill with your use of data?
- What will you do on Monday to begin to address those gaps?
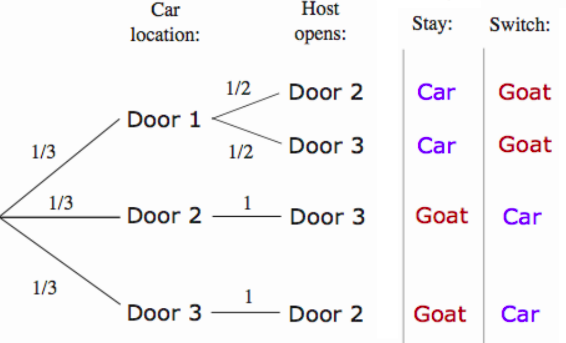
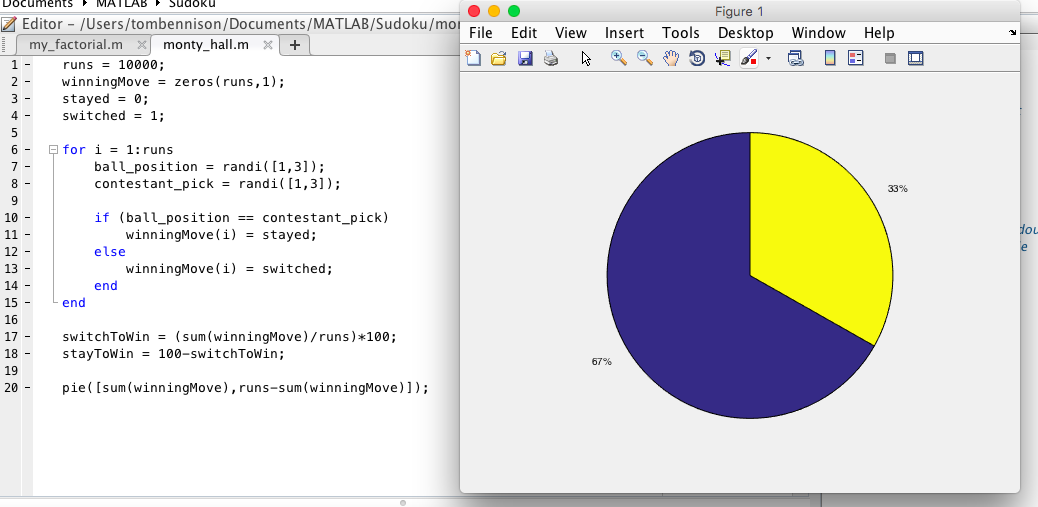
Workshop 2 – Using Software and Games to Inspire and Motivate A-Level Mathematicians: The Case Studies of Sudoku and the Monty Hall Problem
I was co-presenting a workshop in the second slot with Jasmina Lazic. This was an interesting experience as I hadn’t presented a workshop with someone that I hadn’t met face-to-face before today but I think (aside from the technical issues at the beginning of the presentation) it went pretty smoothly. We will write a blog post about the session soon, but here are the slides:
[prezi id=”http://prezi.com/j497g5f6_vep/?utm_campaign=share&utm_medium=copy” align=center width=600 lock_to_path=1]
Workshop 3 – Classroom Culture
Bruno Reddy (@MrReddyMaths) led this workshop and was very prepared and had his PowerPoint slides ready to download before his session. Bruno emphasised that to achieve the fantastic King Solomon Academy results the culture of the department (and school) was key.
The use of clapping as a way of saying well done and getting the class’ attention if they have been working in pairs was something that I had seen Bruno talk about before and I have used successfully in the classroom so it was nice to be reminded of this.
Bruno articulates culture as being what you stand for and how your actions articulate this. The emphasis on culture being from the beginning (or even before) was important, Bruno used some photos of KSA to ask us what we can spot about the culture from the word go. I was particularly drawn to the notices/banners on the ceiling as a way of making some of the cultural beliefs of the school evident. Bruno provided three Questions for reflection:
- What culture is evident in your prospectus?
- What culture is evident from open evenings?
- What culture is evident from your Year 6 days.
I drove back from the conference this evening thinking about these questions, along with many other things!
The use of clicking to provide feedback to the teacher (and their peers) definitely made sense as it is certainly true that students don’t often nod along as you teach them. To me, this would feel strange at first but it is surprising how quickly it begins to feel normal.
Bruno talked about 3 goals for lesson one at the beginning of the year:
- Routineering: Clear entry routines for all classes so that the expectations are there from the beginning. A task present for them to do as soon as they get in. A good entry routine reminds pupils of the high expectations in the classroom. I particularly liked this slide:
 The chance to see Bruno model establishing a new entry routine was fantastic – I am going to try this on Monday with one of my classes and I’m looking forward to seeing how it goes. As the routine begins to slip, he explained how it is necessary to bring this to the classes attention and explain how this would be sanction worthy. Bruno talked about Do Now tasks should give the pupils a chance to achieve and do well to be effective.
The chance to see Bruno model establishing a new entry routine was fantastic – I am going to try this on Monday with one of my classes and I’m looking forward to seeing how it goes. As the routine begins to slip, he explained how it is necessary to bring this to the classes attention and explain how this would be sanction worthy. Bruno talked about Do Now tasks should give the pupils a chance to achieve and do well to be effective.
- Visioneering – “You have to go big with their dreams and win hearts and minds”. I think this is an aspect I would struggle with as to be honest I’m not very good with acting but thinking a head to the beginning of next year I want to give it a go and am going to speak to my head teacher about making a results day video.
- Expectation Setting – Bruno set out two non-negotiables: “100%” and “Every Second Counts”. The “100%” expectation expresses that there is only one acceptable percentage of students following an instruction and that is 100%. I’ve found it hard to stick to this recently but after this session I am feeling re-invigorated 😉 Bruno’s advice to use sanctions for situations where there is a black/white divide is great in my opinion; implementing a sanction for something like an instruction to talk quietly is much harder to do
Workshop 4 – Ask the Exam Board
Eddie Wilde (OCR), Graham Cumming (Edexcels) and Andrew Taylor (AQA) panel discussion. Below I try to present a summary of some of the answers given to a few questions. Unfortunately I felt that about half of this session was wasted as they were answering questions that have either been (very) publicly answered before or the answers have been in published materials, but it was interesting to hear a more human take on them.
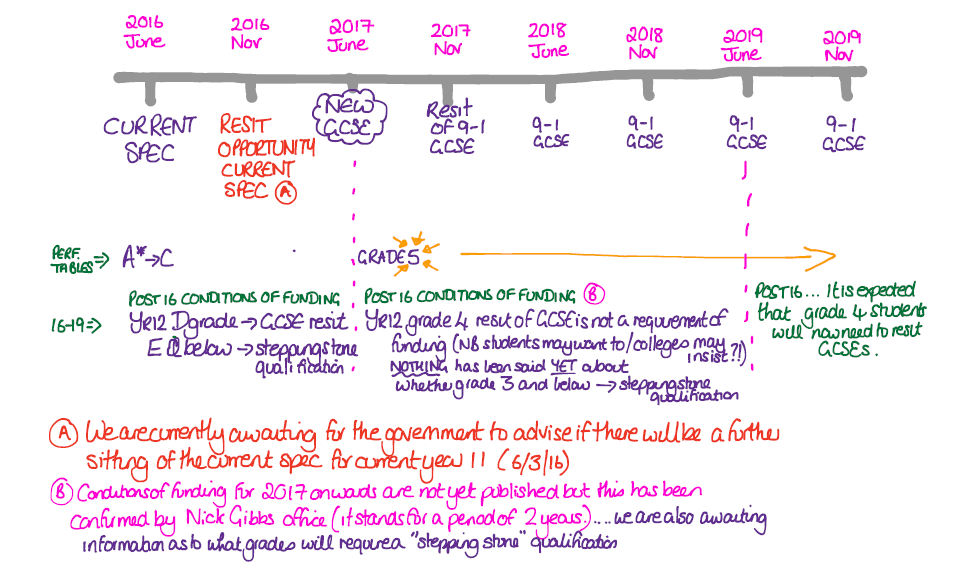
- What do the new grades look like? Will there be grade descriptors? GC – “we do not know what the boundaries look like, we can model them to an extent. We know roughly that 4 <-> C as Ofqual have stated earlier. They know that the ramping of difficulty will be different to current papers. Foundation papers up to Grade B, Higher to start at Grade C. AT – If we put a 9-1 grading on last years cohort we could see how the grades fall out, but it is a completely different system so it is an unknown. We are required to have 50% of the higher exam targeting grade 7 and above but it is hard to see how this will translate to student performance. EW – Individual questions will not have grades attached, it doesn’t happen now and it won’t in the future.
- How are we supposed to assess progress with current students? EW – For a strong Grade C candidate you are looking at a 4/5. All boards have ways to assess current students, eg Edexcel’s Check In Tests. But they will not translate into grades on the 1-9 scale. GC – All boards to have mock papers written for October, papers designed for students close to the end of Year 11. I particularly liked this quote from Graham “Hannah’s Sweets will be Question 1 on all our papers now”. AT – The ordering of pupils using old style assessments may not necessarily carry over to the same rank order in 2017 due to the different style of assessments.
- Can we have some guidance on what tier we should enter students for? AT – This is a common question at the moment. 10% of students getting a grade on higher tier on the current specification ended up with a U when matched up with the new style of assessments (it is currently around 1% to 4.5%). EW – If genuine C/D borderline students he would put them in for foundation as they could expect to be able to do about 2/3 of the paper, but he doesn’t want to tell you what to do. GC – If you want to use a current paper, look at the Results Plus data and chop off the first 20 marks to give an indication of how they would do on a new 80 mark paper. This would be optimistic though due to the changing of style.
- How many forms can questions about bounds and limits take? GC – “The possibility for bounds questions is of course unbounded”. Questions on this topic can be very simple but can be top grade questions. The higher grade questions are likely to be similar to current questions. Edexcel are trying to cover every style of question through their practice papers that they are releasing. One of the assessment objectives is to talk about assumptions, if a question was demanding more interpretation or analysis it would occur later in the paper. EW – Questions are not designed to trip students up.
- Trial and improvement, in or out? EW– Trial and Improvement is a perfectly valid technique but it is no longer a required technique in the new specifications so students could use this unless the question directs students to use another technique, eg iteration. AT – Trial and improvement is part of iterative methods which is only on higher tier content, and so questions that now involve trial and improvement must be set at a level to appear on the latter half of the paper (unlike the current “draw a trial and improvement table for this question).
- Truncation – one question from OCR, are there others? Is truncation not as important as others? EW – the fact that something appears in a SAM doesn’t indicate an order of priority in terms of content.
- Will there be an alternative maths qualification for those students who would not achieve at GCSE standard? – EW – Four is the new “good” for the first two years with the expectation that it will change to 5. Only the top third of those students who currently get a grade C are expected to get a 5. AT – Entry Level Certificate has been re-developed in parallel with the new GCSE specification and will be there to be used. We don’t know if students will be evenly distributed in the grade 5, it is an arithmetic thing. Grade 4 and 5 are comparable across the tiers and so parity will be achieved through common questions etc. GC – Edexcel have the Level 1 awards in Number and Measure alongside Level 1 qualifications in Functional maths.
- What are your views on the up coming changes to the new A Level? AT – we don’t have enough time. There are pros and cons to both modular and linear approaches. One of the pros to the modular approach is the increase in uptake for A Level maths and further maths in particular. Ofqual are very close to providing final guidance on assessment conditions.
- What can teachers be doing differently? AT – Teach well and concentrate on that. When a team of teachers are coming together before teaching a topic go to the spec and decide how to teach so it is not a walk in the park for top sets or how to bring it down to a lower level for lower sets.
- How do I promote a love of maths? EW – easy, enjoy it yourself and promote this to the kids. GC – show kids that they can love it. AT – Teach the subject and not how to pass exams.
Other Fun Aspects of the Day
The Tweet Up was enjoyed by many and it was great to catch up with Kyle McDonald (@jk_mcd) from Wellingon College and be told about their Harkness resources for A-Level. Sample versions of these are available on their website and further information can be obtained from Aidan Sproat (@AidanSproat).
I was also pretty excited to meet the Corbett Maths (@corbettmaths) in the lunch break.
It was lovely to finally meet Naveen Rizvi (@naveenfrizvi) and have a decent conversation with her in the bar after the event. I also enjoyed chatting with Neil Turner (@Mr_Neil_Turner) about various teaching related topics.
I ended the day with a lovely catch up with Jo Morgan (@mathsjem) before dropping her off t the station and driving home. Jo has just published her 50th “MathGems” post and Julia (@tessmaths) organised the most amazing cake for her!

I also got possibly the best conference freebie ever today courtesy of OCR:

All in all a fantastic day and I’m looking forward to the next one in Leeds.