A good friend of mine, Ed Hall had told me about a lecture at the University of Leicester this Tuesday (10th February 2015). This lecture was the 17th Annual Industry lecture organised by department of Engineering and was given by Professor Dame Ann Dowling. Professor Dowling is President of the Royal Academy of Engineering and a professor of engineering at the University of Cambridge where she ran the University Gas Turbine partnership with Rolls-Royce between 2001 to 2014. She is a world authority on combustion and aero acoustics and researches efficient, low emission aero turbines and low noise vehicles among other things.
The lecture hall was completely packed, I’m guessing over 200 people were in attendance. Professor Dowling started the lecture by showing how the noise from modern civilian airliners is significantly lower than that from airliners of the early jet age and thar they are also more fuel efficient.
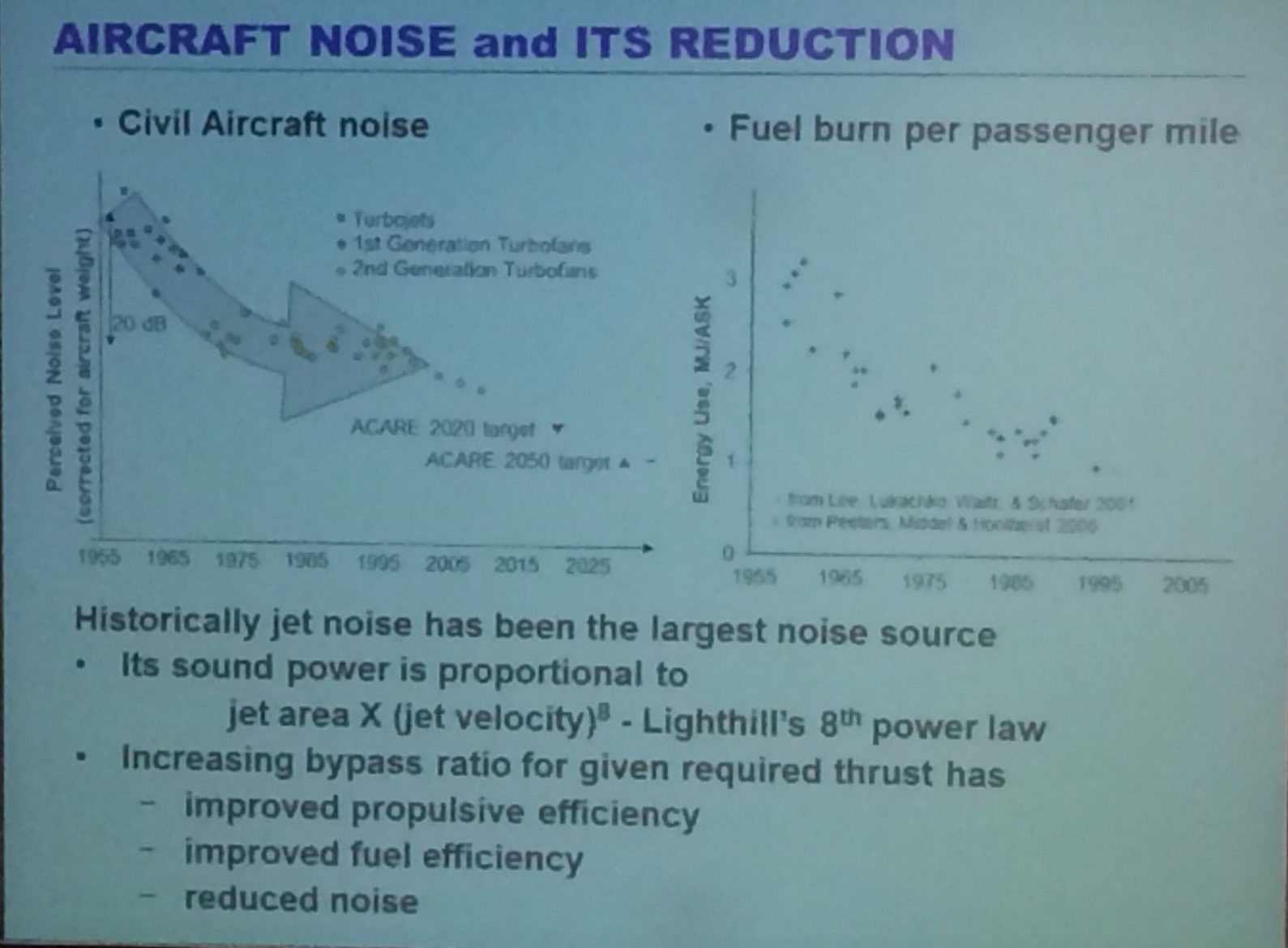
As you can see from the graph, this decrease in noise has plateaued (is this a word!?) in recent years. Perhaps a reason for this is that environmental concerns have led to an increase in attention paid to improving efficiency, she mentioned that increasing the size of the engines has increased fuel efficiency but increased the noise level (from the large fans).
More recently, during take-off the noise of the rear jet has been balanced by the noise of the fan at the front of the engine (on approach the noise of the airframe becomes significant too, I will be doing a write up of another talk which discussed this in more detail), and so, the noise of the rear facing jet is not the only thing to be controlled.
Below is a section diagram of the Rolls-Royce Trent 1000 (the picture is taken from their excellent infographic which is available here), I have included it here as I will refer to some of the key components.

The large size of the fan – ~2.8m for the Trent 1000 – contributes to the large noise from the fan, so making this as light as possible can help, for this reason Rolls-Royce now use hollow fan blades with an internal girder like structure. Something, that to me is less obvious, mentioned by Professor Dowling is the noise generated by the wake from the fan impinging on the static stators that are downstream of the fan. This can apparently be improved by designing the stator so that the wake hits them at different points leading to the different frequency components of the noise cancelling out (this is how I understood it anyway – I am not an aero-acoustic engineer!) – this is very cool! Modern jet engines also often have chevrons on the trailing edge of the jet nozzles to reduce noise by smoothing the mixing of hot and cold air, since the source of the noise is the velocity fluctuations in the air coming out of the nozzle. However, these are generally designed empirically since running a full large eddy simulation of a jet flow through a chevron-ed nozzle takes around 4-6 months on a national supercomputer. Professor Dowling’s team developed a far quicker method that was validated experimentally.
She then presented the SAX-40 concept design for a silent aircraft:
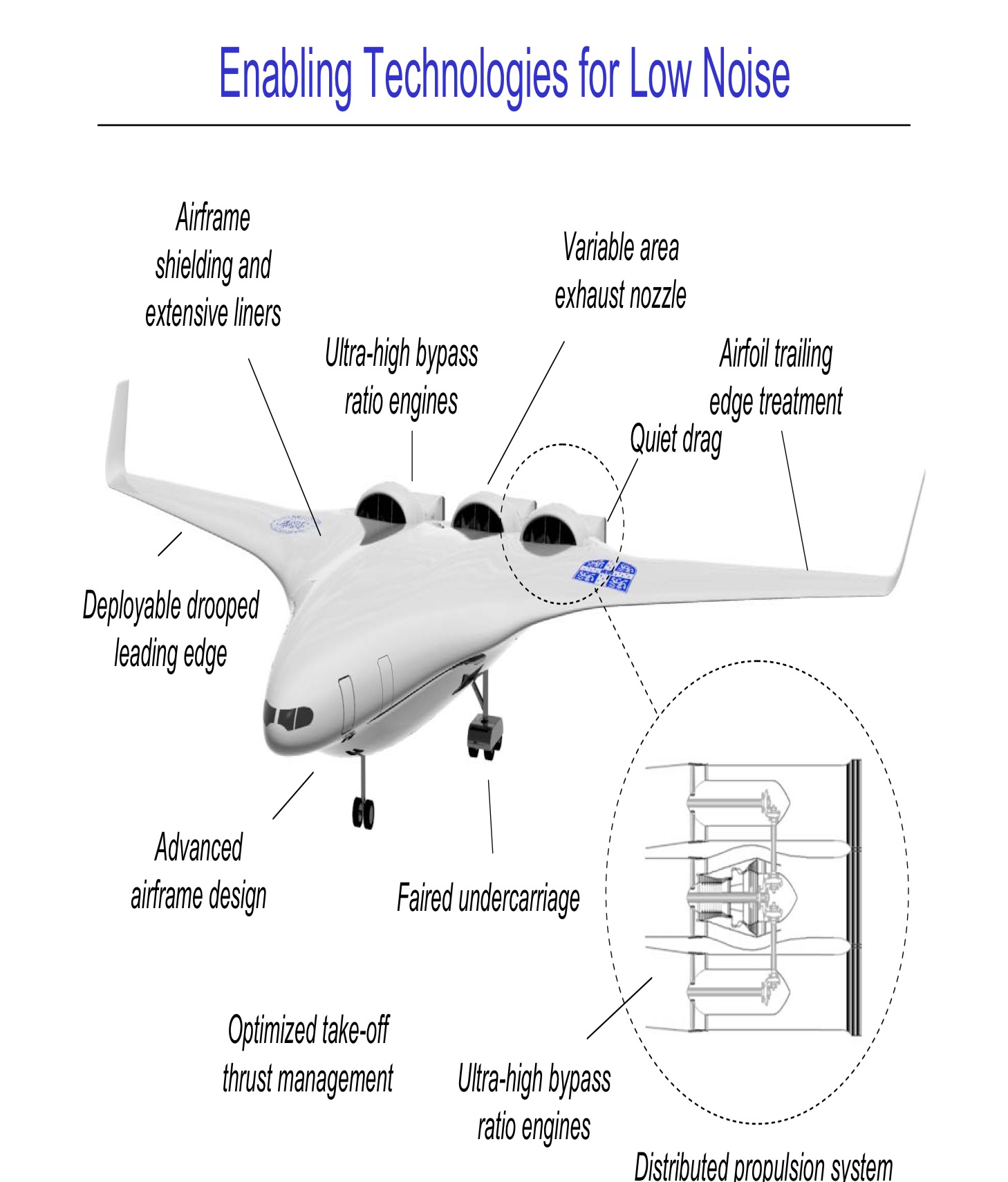
This image is taken from some slides available here. As you can see, this looks very different from todays conventional jets!
As the engines are buried inside the airframe, instead of in nacelles hung below the wings the airframe can be used to shield some of the noise, with more space being given over to the use of acoustic liners to contain the noise. The noise from the engines would also be reflected above the aircraft reducing the noise level when compared to a conventional aircraft even further. The wings of conventional planes reflect the noise below the aircraft and towards the ground. As mentioned earlier, the airframe noise is significant when a plane is coming into land; one factor contributing to this is the use of the flaps and slats on the wings which introduce large holes into the wing surface – the air flowing around these holes creates a lot of noise. For this reason, the concept features a deployable drooping edge.
The noise due to the undercarriage of an aircraft is also significant and Professor Dowling’s researchers looked into this too. To accurately measure the source of the noise from the undercarriage they installed 108 microphones in a section of floor from an aircraft which could then be used in a windtunnel. The undercarriage of modern civilian jets are pretty similar with most having multiple wheels that are exposed. The analysis discovered that having two wheels produced the largest reduction in noise, however this obviously limits the weight that can be born by the undercarriage. So, a design with the rear set of wheels staggered inside of the front, different shaped wheels at the front and rear and a fairing were found to reduce the noise from the undercarriage significantly.
This talk was very interesting and thought provoking. However, I’m not convinced we will ever see a plane like this due to how radical it is!!
It was also nice that there was a buffet reception after the talk where I had some interesting conversations with a retired engineer – you can’t beat free food! I had also been lucky enough to arrive in Leicester early and have time to talk to Ed about upwind fluxes, Runge-Kutta time stepping methods, discontinuous Galerkin methods and the Navier-Stokes equations – all exciting topics which I don’t have much of an opportunity to talk about anymore.