The Japanese method of multiplication seems to be everywhere at the moment – Julia (@tessmaths) I noticed had advocated it ( I think prompted by a tweet by @missradders) on Twitter overtone weekend and one of my oldest friends posted a video of it on my Facebook page yesterday asking how it works and if it will always work.
This method is apparently taught to Japanese primary school pupils (note to self: ask the Japanese exchange pupils when they next come!) as an easy method for multiplying large numbers (larger than the times tables anyway).
It works due to the way that numbers are written down in base 10. For example, 325 is 3 lots of a hundred plus 20 lots of ten plus 5 lots of one. This along with the distributive property of multiplication allows us to split numbers up when multiplying. If I was working out 24 times 12 mentally I would split it up into two multiplications – 20 times 12 and 4 times 12 – then add the results. Mathematically, this can be written as:
\( 24 \times 12 = (20 + 4) \times 12 = 240 + 48 = 288 \)The Japanese method takes this a step further and says that both numbers can be split up in this way and so that
\(\) 24 \times 12 = (20 + 4) \times (10+2) = 20 \times 10 + 20 \times 2 + 4 \times 10 + 4 \times 2 = 200 + 40 + 40 + 8 = 288 \(\)
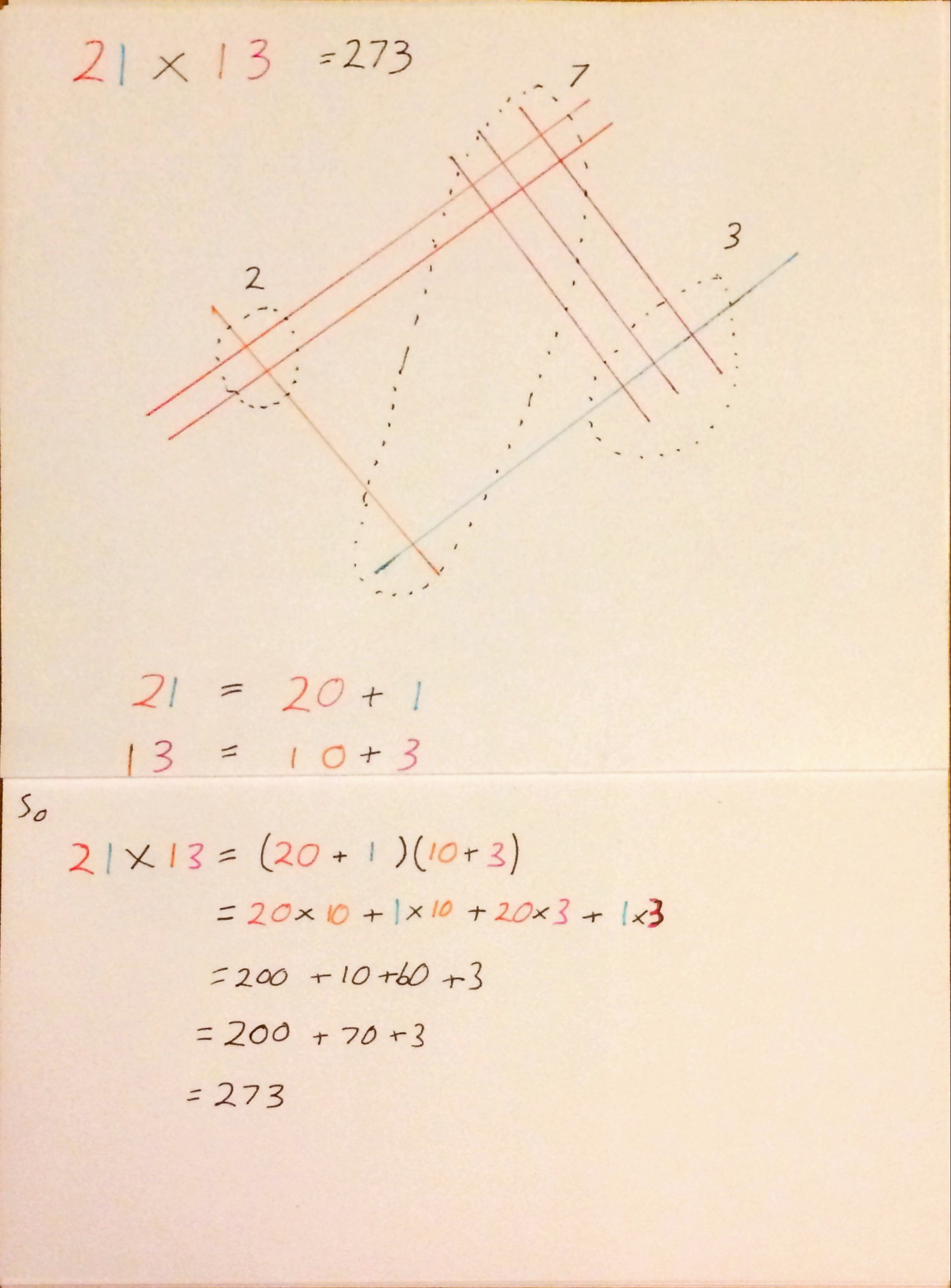
To multiply using the Japanese method you represent 24 as two parallel lines, a large gap and then another parallel line and represent 12 as 1 parallel line with a gap then 2 further parallel lines. The lines for 24 and 12 cross each other. Then to calculate the product you count the intersections on the right for the units column, the tens is calculated by combining the two sets of intersections in the middle and then the number in the hundreds column from counting the intersections on the left.
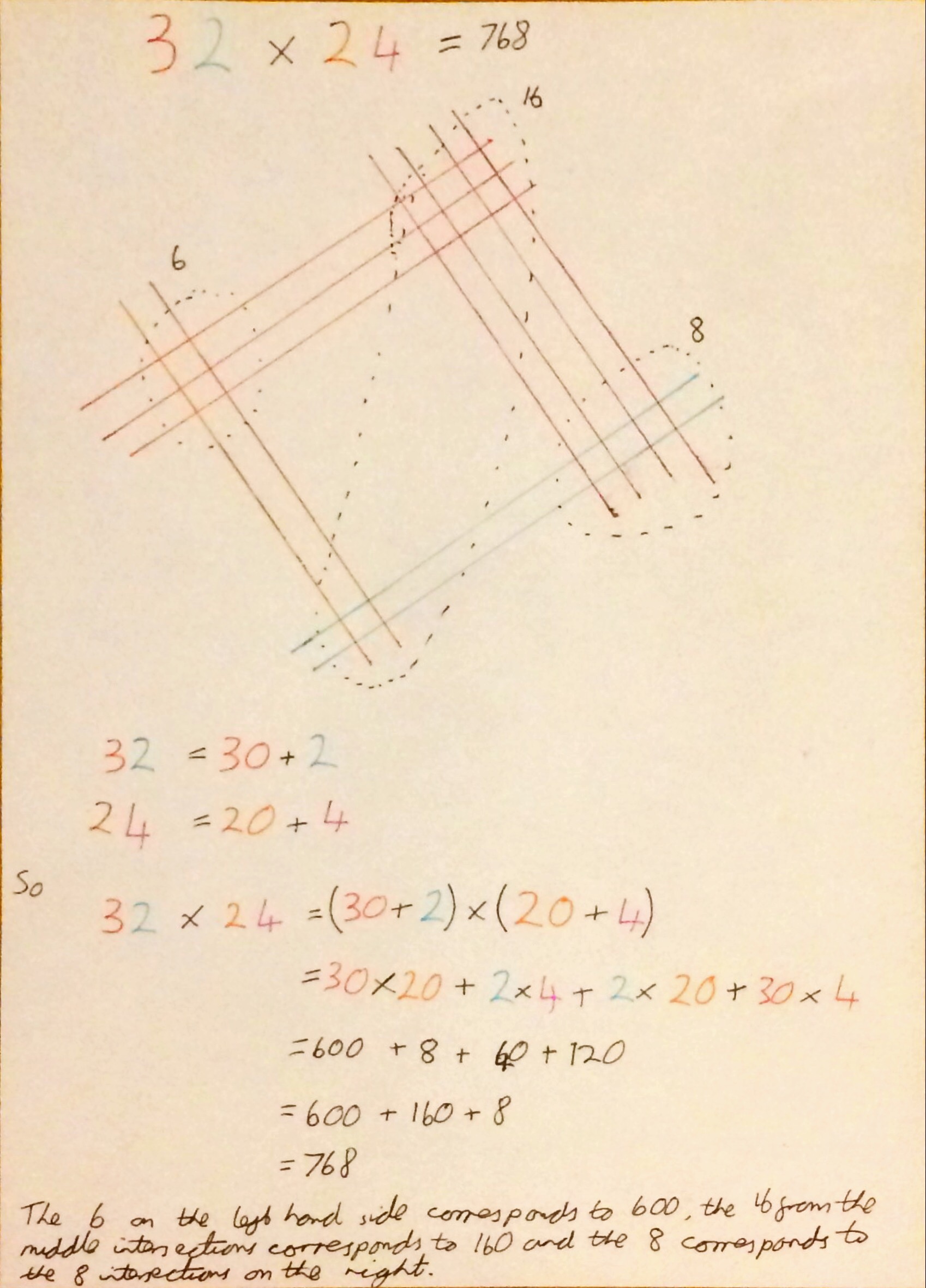
I think that makes a lot more sense in a picture, so here is another example:
In the example above the number of intersections in the middle is 16 and so 10 of them have to be carried to the left, increasing the number of hundreds from 6 to 7.
For larger numbers this method becomes incredibly cumbersome – what withdrawing all the lines, counting intersections and dealing with the carries. See the example below for two 3 digit numbers:
 I much prefer the lattice/Chinese/Napiers Bones method myself, but that is for another day.
I much prefer the lattice/Chinese/Napiers Bones method myself, but that is for another day.