Many people came out of this exam saying it was hard, even some of my FM class said they didn’t particularly enjoy it. Compared to the 2014 paper i do think it was a bit harder; the lack of a question concerning the trapezium rule was a noticeable omission of some easy marks.
Starting on a question by question basis, Question 1 was a straightforward application of the binomial expansion, only requiring 3 terms to be given. This is esppecially easy as you are given the binomial expansion in the formula book! I think this was a very nice start ot the paper and hopefully would have boosted the confidence of the students sitting the paper.
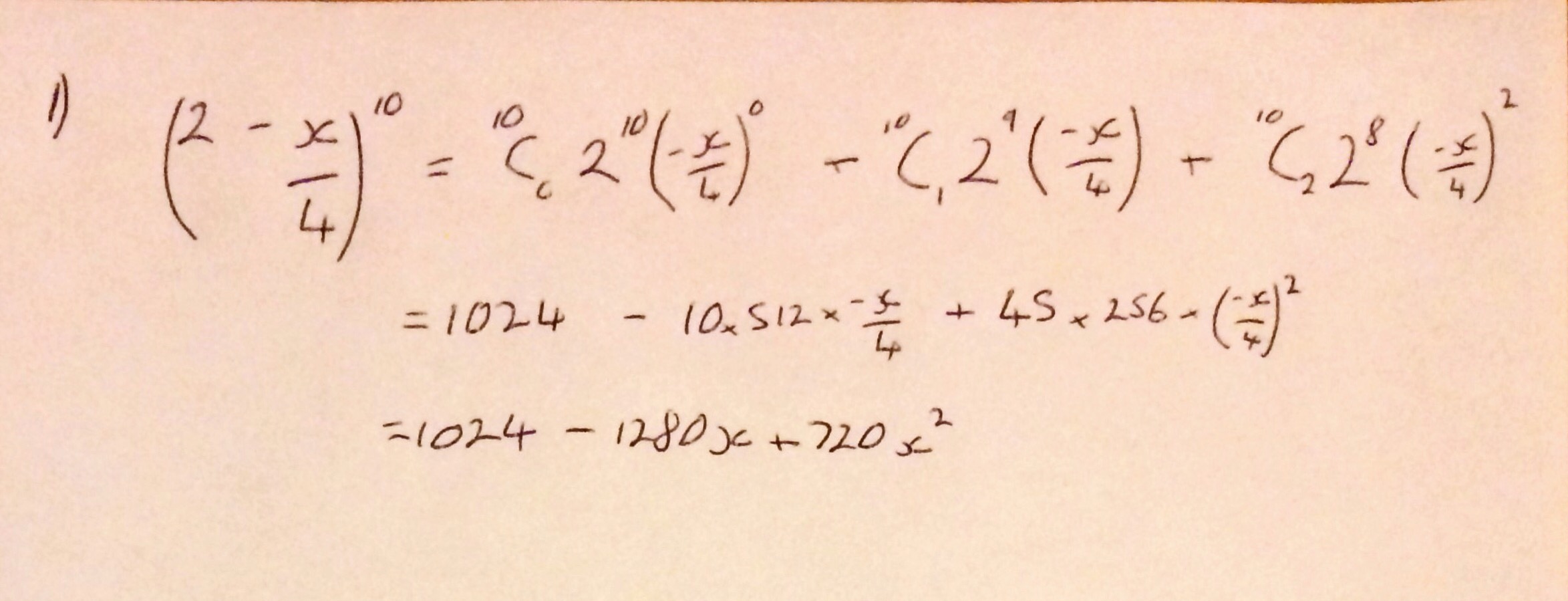
Moving on to question 2 we had, what I think, is quite a nice circle geometry question. Finding the equation of the circle is straightforward, given that you are told the centre and a point on the circle – conceptually I think this is easier the starting part of the equivalent question last year. We then go on to find the equation of a tangent to the circle requiring a bit of memory of circle theorems from GCSE and the properties of perpendicular lines.
Some students that I have spoken to have said that they found Question 3 hard, it is definitely more challenging than the equivalent 2014 question, however it is almost identical to the corresponding question in the 2013 paper. Just use the remainder theorem and factor theorem to form two equations in terms of \(a\) and \(b\) and then solve. It factorises nicely, into the factor given and a differenc of two squares (as long as you recognise that a factor of 3 can be pulled out).
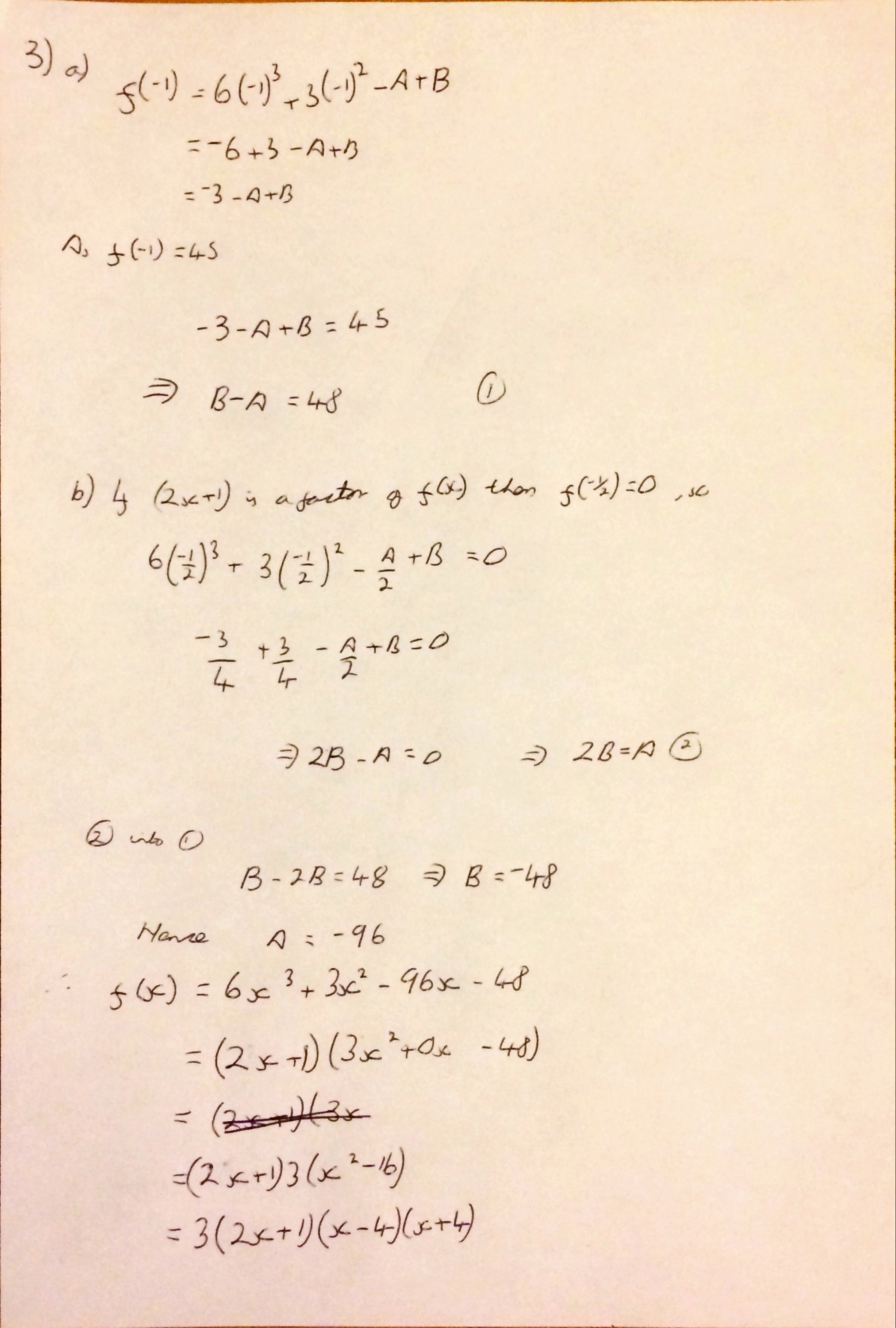
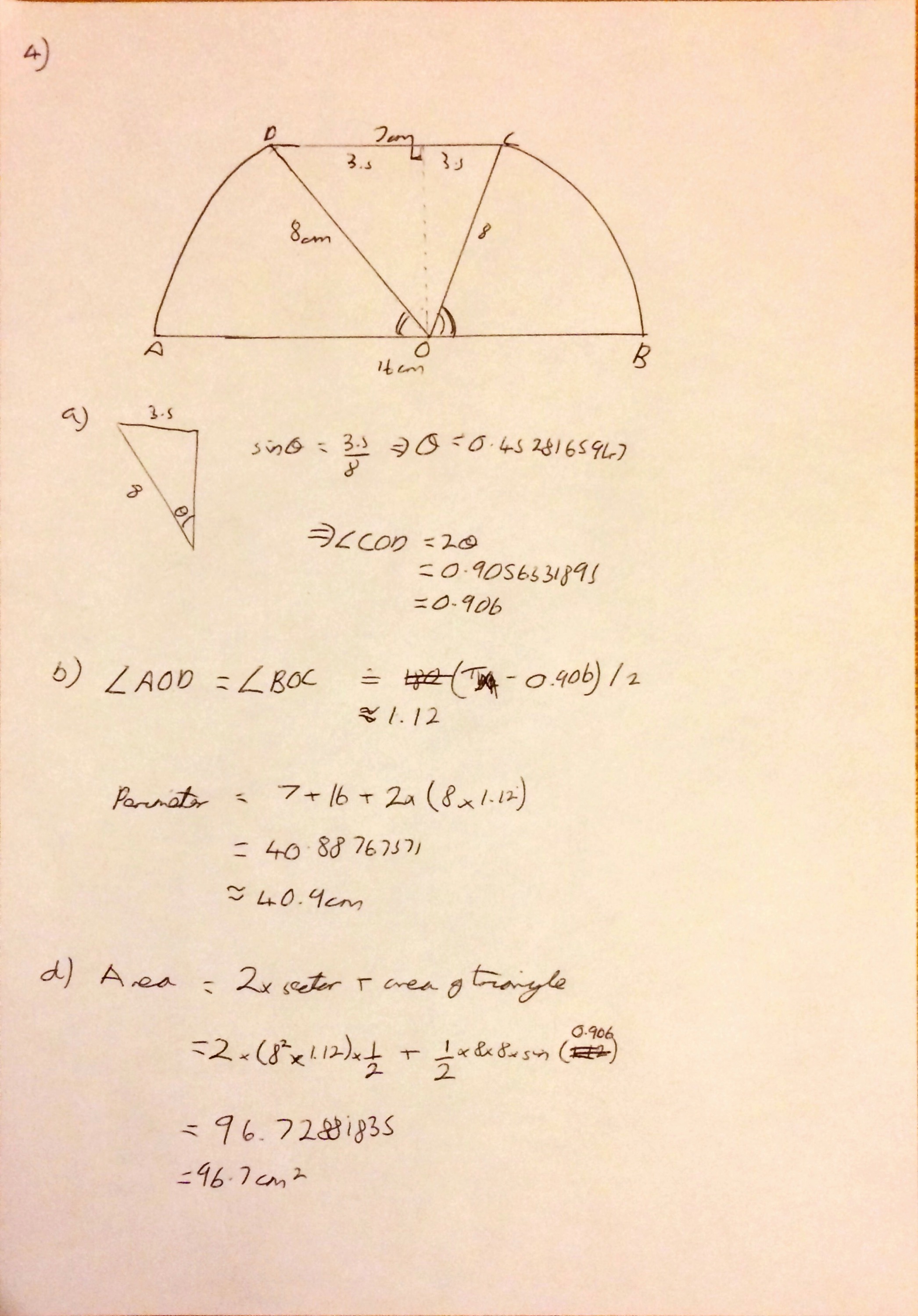
The area and perimeter of sectors question (Question 4) seems fairly typical to me, I think some may have found the first part of the question a bit tricky, and won’t have thought to break the triangle into two right angled triangles and then double it. Once the angles have been calculated, completing the rest of the calculation is fairly simple. I guess some may have forgotten to add the base length in when calculating the perimeter. Please marvel at my awful diagram for this question, and note I used the incorrect angle for the last part at first!
Question 5 concerned geometric series and to me feels harder than the equivalent question last year. However, as the formulae are all given in the formula book, forming the equations (simultaneous equations again!) required for the first part shouldn’t be too difficult, and solving them drops out nicely. The second part of this qquestion requires a bit more thought and the use of logarithms to efficiently solve – I also think a few people will have forgotten to round up to the nearest integer.


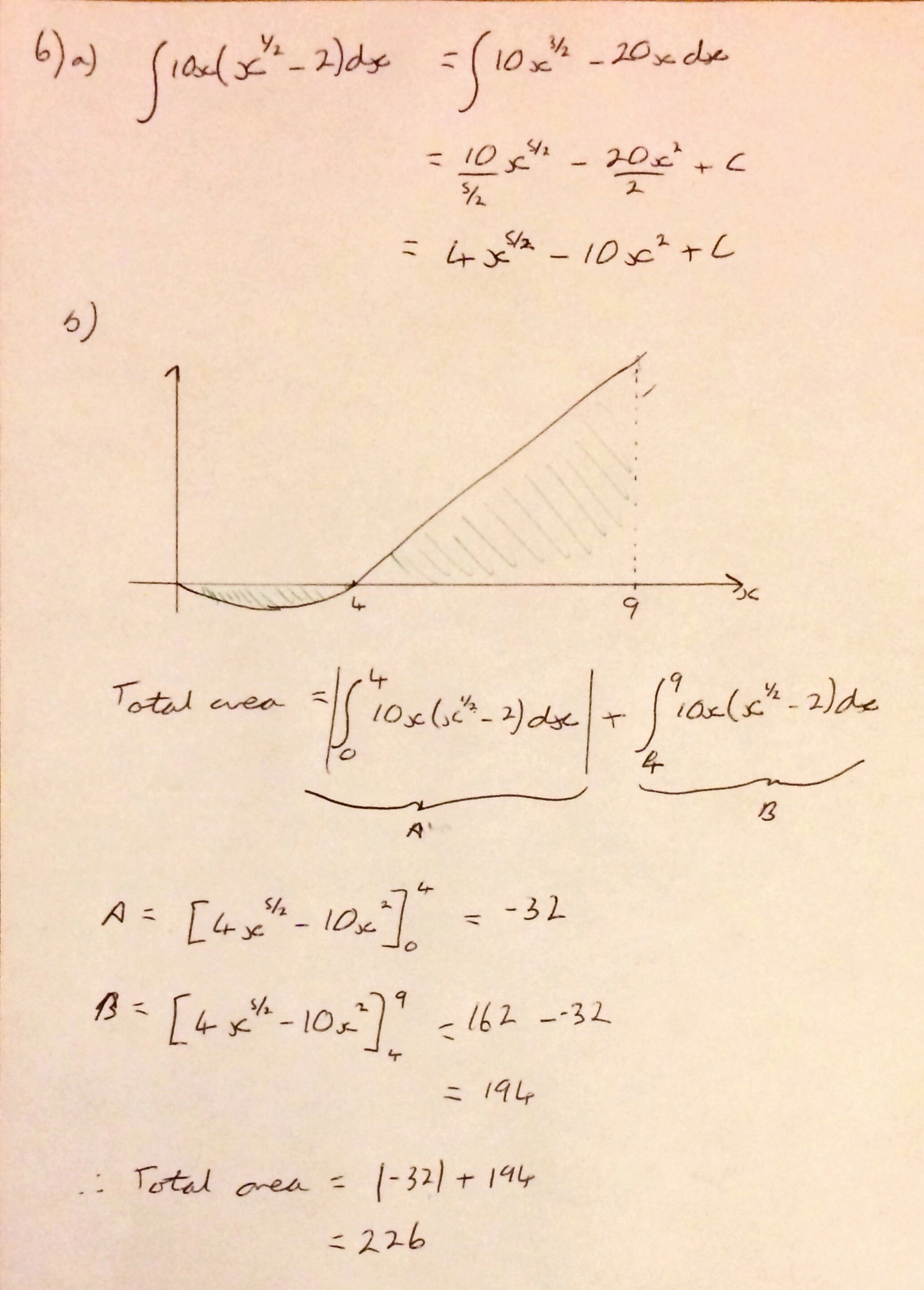
Question 6 moved on to integration and finding the area under a curve. They even gave you the points where the curve crossed the axis and a very helpful picture of the shaded region to find the area. The tricky part I imagine would be remembering to take the absolute value of the area of the first region when working out the total area.
Question 7 was the main logarithm question and I think this was slightly easier than the last two years as it was obviously a logarithm question and no curve sketching was required. As long as students are systematic in their application of the logarithm rules part b should be ok, though there are plenty of places for arithmetic errors to creep in.

I think the trigonometry question will have thrown a few people: you don’t often see \(3\theta\) in a question, but apart from that part a is ok as long as they remember the period of \(\tan (3\theta) \) is a third of that of the period of \(\tan ( \theta) \). The phrasing of part b seems to have confused a few people, but once you have got to a quadratic in \( \cos x \) the solutions drop out nicely.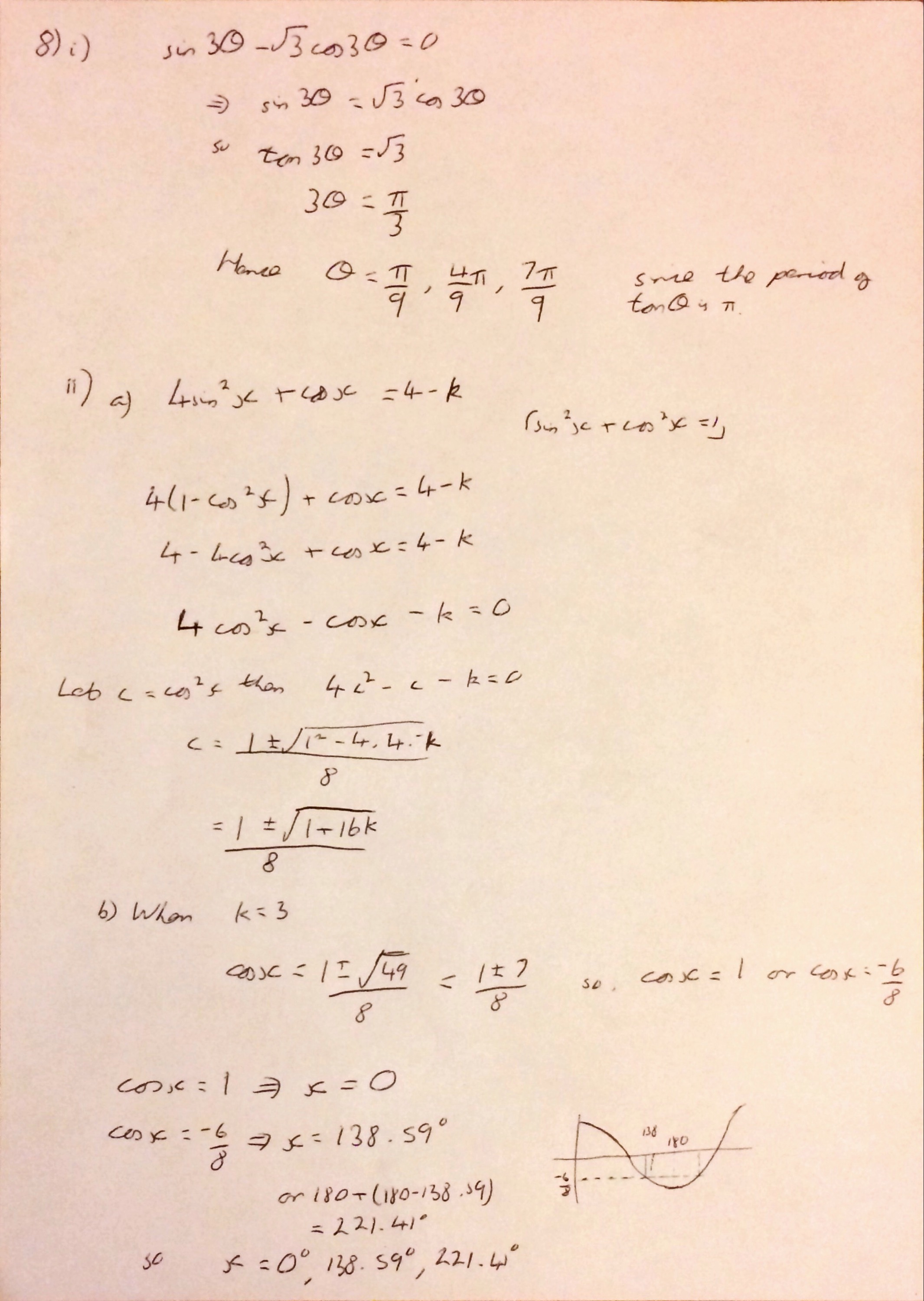
The final question was very similar to the last question on the 2014 paper – in that it concerned minimising a function of the surface area of a 3D shape. Minimising it and checking the nature of the stationary point is straightforward and these marks could be picked up even if the candidate hadn’t managed to derive the expression for the cost of polishing themselves.
Overall a nice paper, a bit more challenging than some recent ones in places but generally it seemed pretty fair. They are liking simultaneous equations at the moment.
A scan of the questions is here and a pdf of my solutions (complete with my incorrect attempt of Q5b) available here.


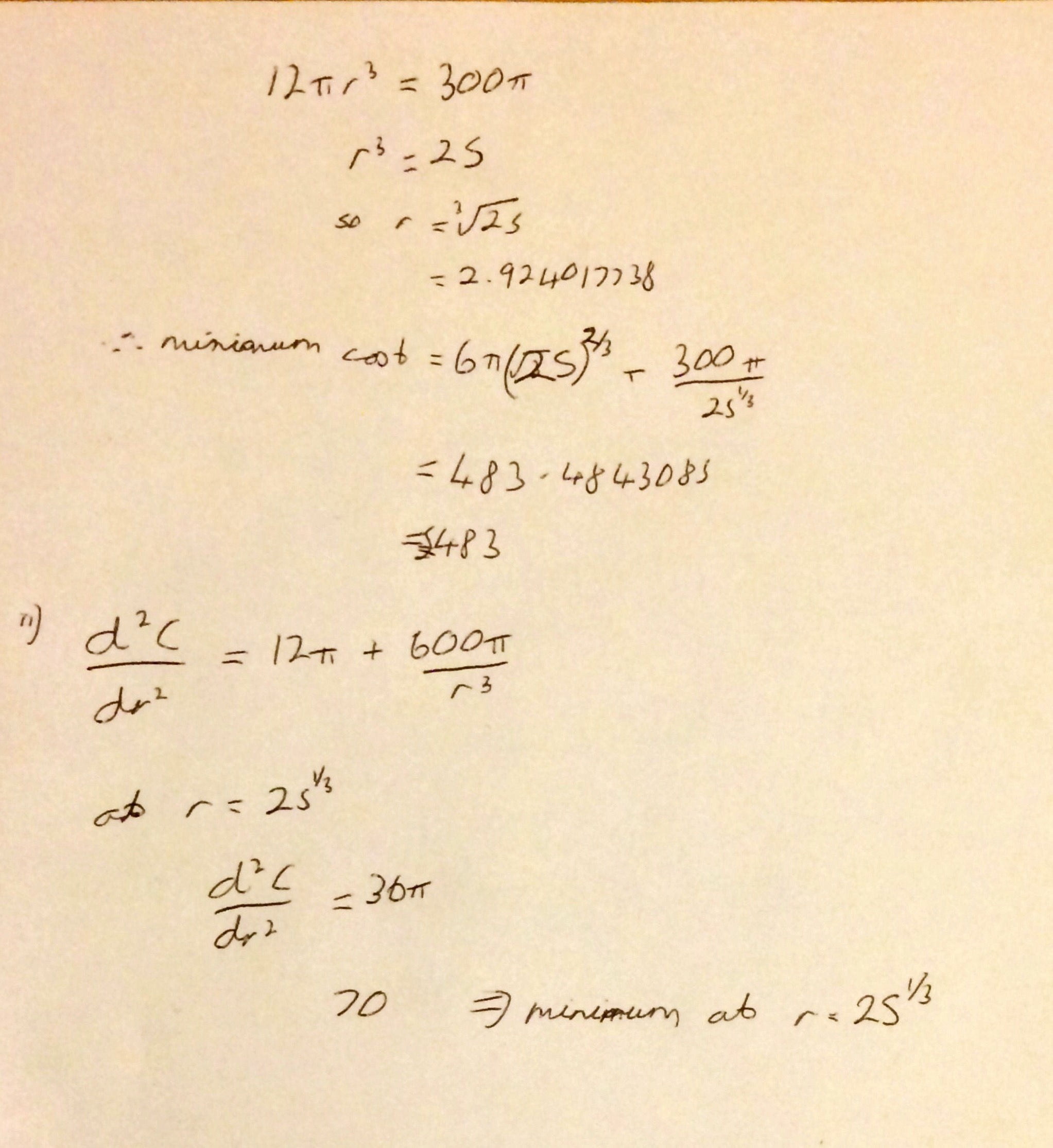
3 replies on “Thoughts on Edexcel Core 2 2015”
Nice reflections Tom, did you see my post on the questions that annoyed me?http://wp.me/p2z9Lp-u9
Regrading the sector question, why did you split it in two for part a and not use the cosine rule?
And wasn’t it bizarre that neither c1 nor c2 had any graphs questions. (Bar a 2 marker on c1)
I hadn’t – but I now have and have left a comment 😉 nice post. And no idea really, the cosine rule just didn’t come into my head – I need to use them more I think, I often make things more difficult by trying to create right angles!
And yes, very odd – they’ve given so many pictures this year.