Earlier on today I took the picture below of my tea cup (Lipton Passionfruit and Raspberry black tea, brought back from Madeira if you are interested)

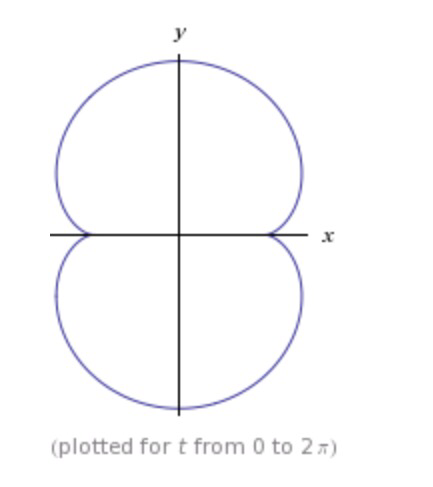
I’ve always liked seeing this pattern at the bottom of a tea cup and I’m sure many of you recognise it as an example of a caustic curve. This is the envelope rays of light reflected on a curved surface. In fact, the curve shown above is half of a nephroid (the name is derived from the word for kidney shaped( as shown in this plot from Wolfram Alpha
Mathematically this curve is defined by the following equations
\( \begin{align} x(t) &= a(3\cos (t) – \cos (3t)) \\ y(t) &= a(3\sin (t) – \sin (3t)) \end{align} \)
with cartesian curve
\( (-4a^2 + x^2 + y^2)^3 = 108a^4y^2 \)
You may have plotted these curves in school as they are a popular “stitching pattern”. Namely, place \(n\) points equip-distributed around the circumference of a circle, and then work round the circle joining the \(n\)th point to the \(3n\)th point with straight lines. I’ll do one as an example at some point and post it on here.
In the mean time just marvel at the fact that such a cool curve appears at the bottom of a cup of tea! The light rays need to meet the cup at a very precise angle to obtain this curve – in fact tilting the cup gives some nice curves as they transition into and out of a nephroid.