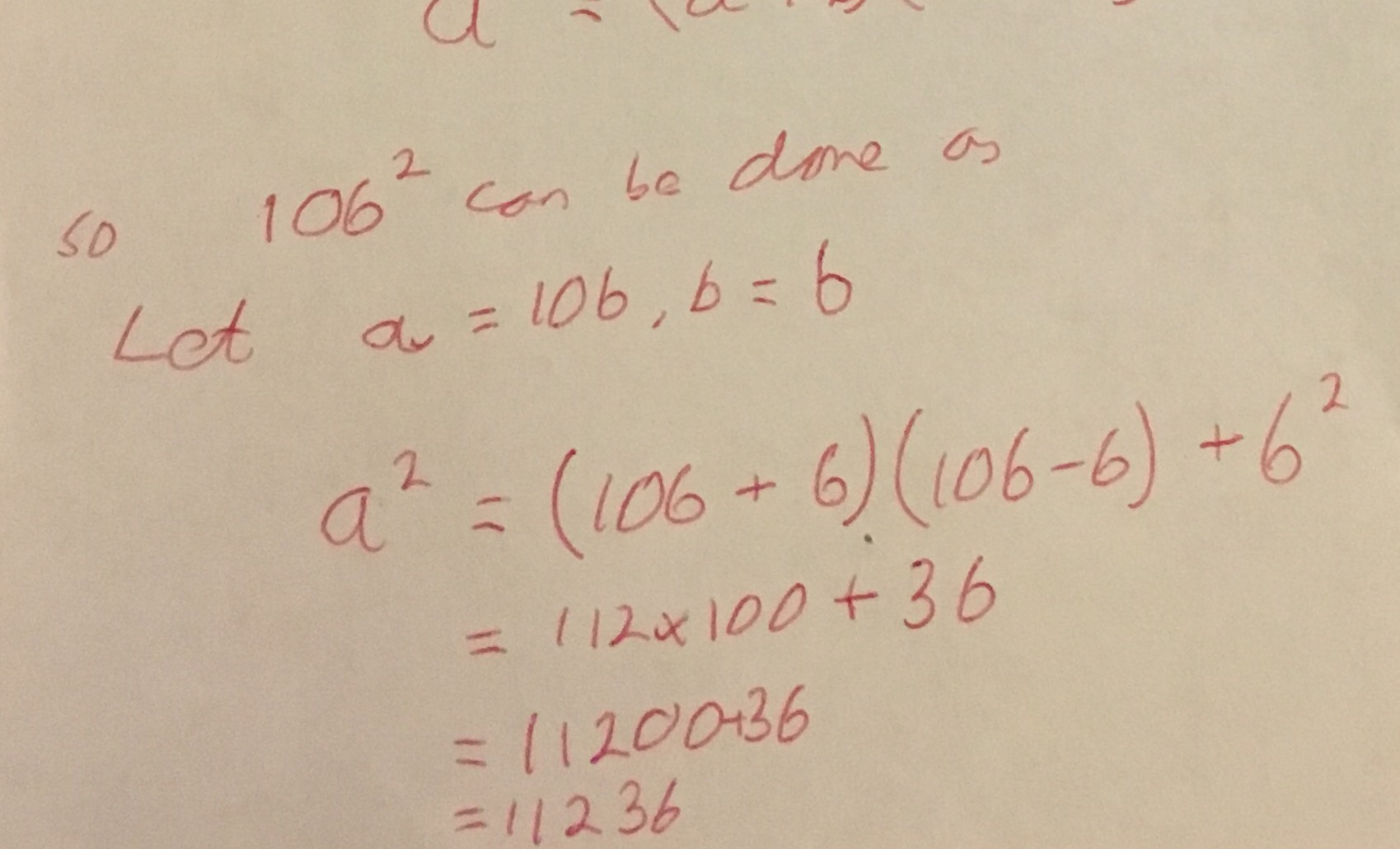This Wednesday was the Nottingham Regional Final of the UKMT Senior Team Maths Challenge and I was lucky enough to take my team of Sixth Formers who did really well (a very proud teacher here!).
I thought I would quickly share a couple of simple tricks for squaring numbers, which I am sure that most of you will know but I had never really had much of a need for things like this until I started preparing teams for this kind of thing.
The first one is for squaring numbers that end in 5. For any number ending in 5 take the digits before the five, call this \(n\) and then multiply by \(n+1\) before appending 25 to the result. For example for \(325^2\) work out \(32 \times 33 = 1056\) and so \(325^2 = 105625\). To show why this works just consider the following.
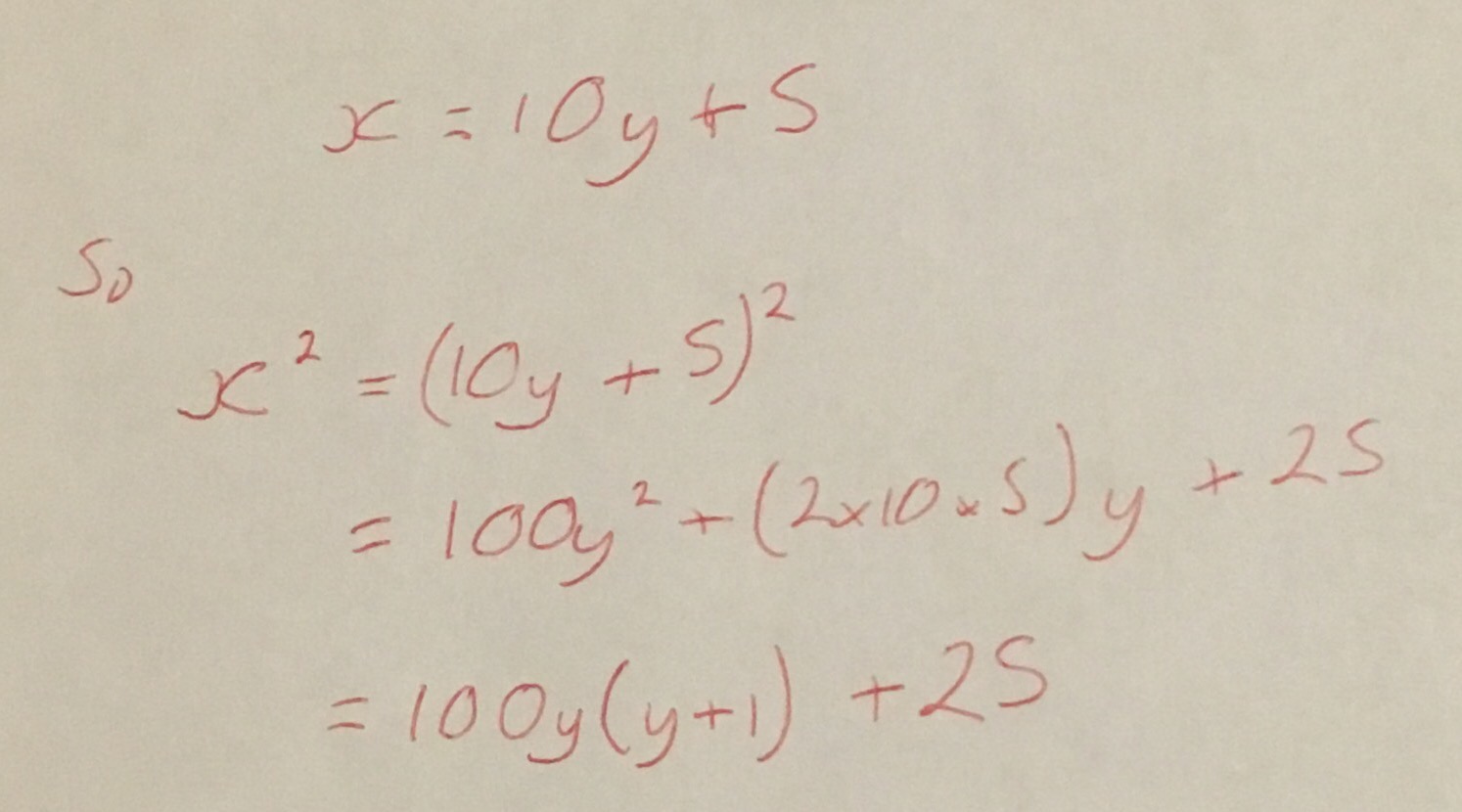The last line of this is merely the product of \(y\) and \(y+1\) with 25 appended to the end.
Another trick makes use of algebraic identities to change the squaring of an arbitrary number into some easier squaring operations.
Consider \(a^2 = (a+b)(a-b) + b^2\). This can be used to help us work out some squares, for example:
