This post mainly concerns the use of WolframAlpha and has been prompted by a tweet by Peter Rowlett on the 10th of December 2015.
WolframAlpha is an incredibly useful tool that more and more students are beginning to use to check their work (and, I’m sure in some cases just do the work for them!) and the free from input that is a large part of WolframAlpha’s mission makes it very easy to use.
However, sometimes this natural language free form output doesn’t result in what the user expects as this tweet from Peter (@peterrowlett)
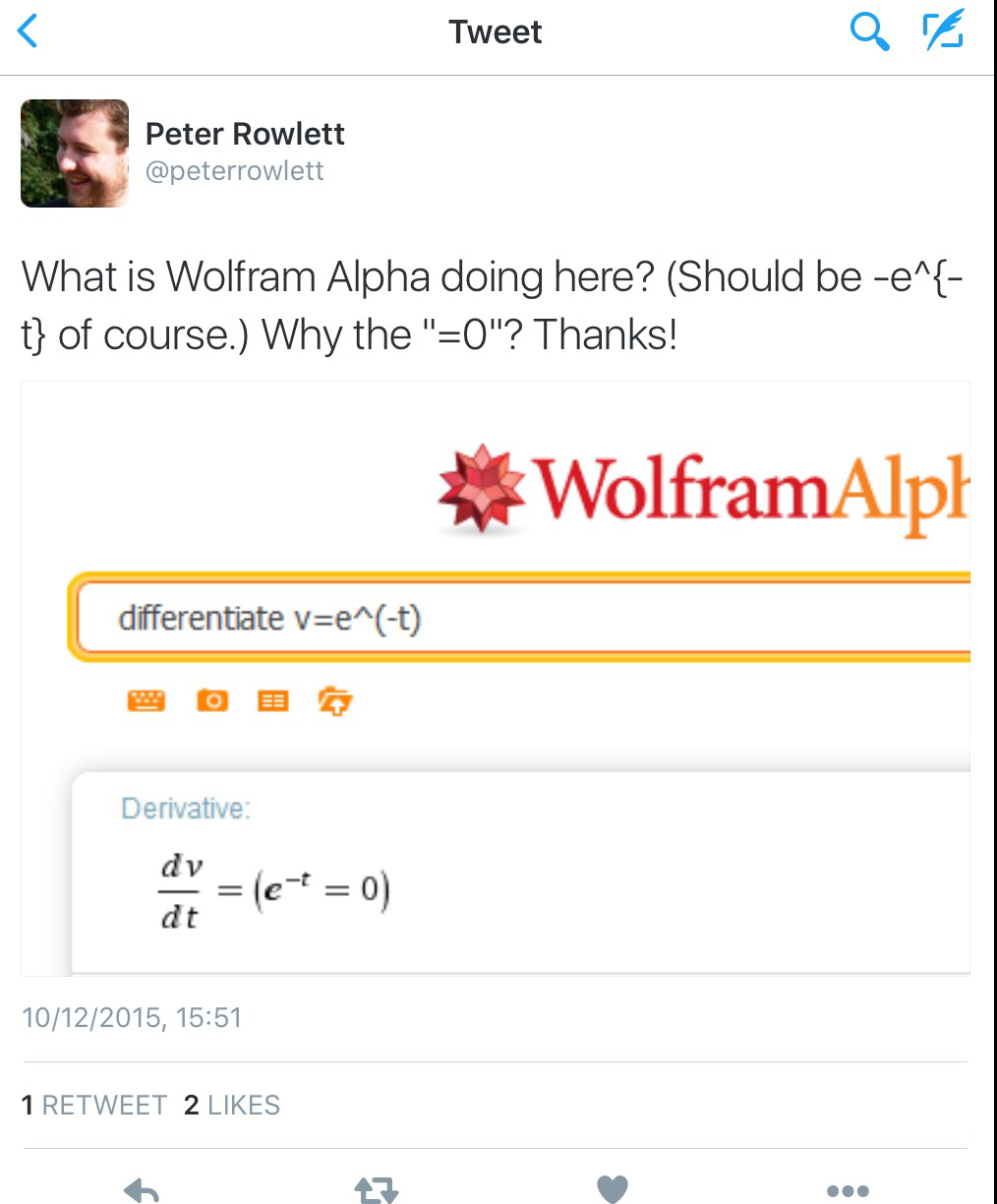
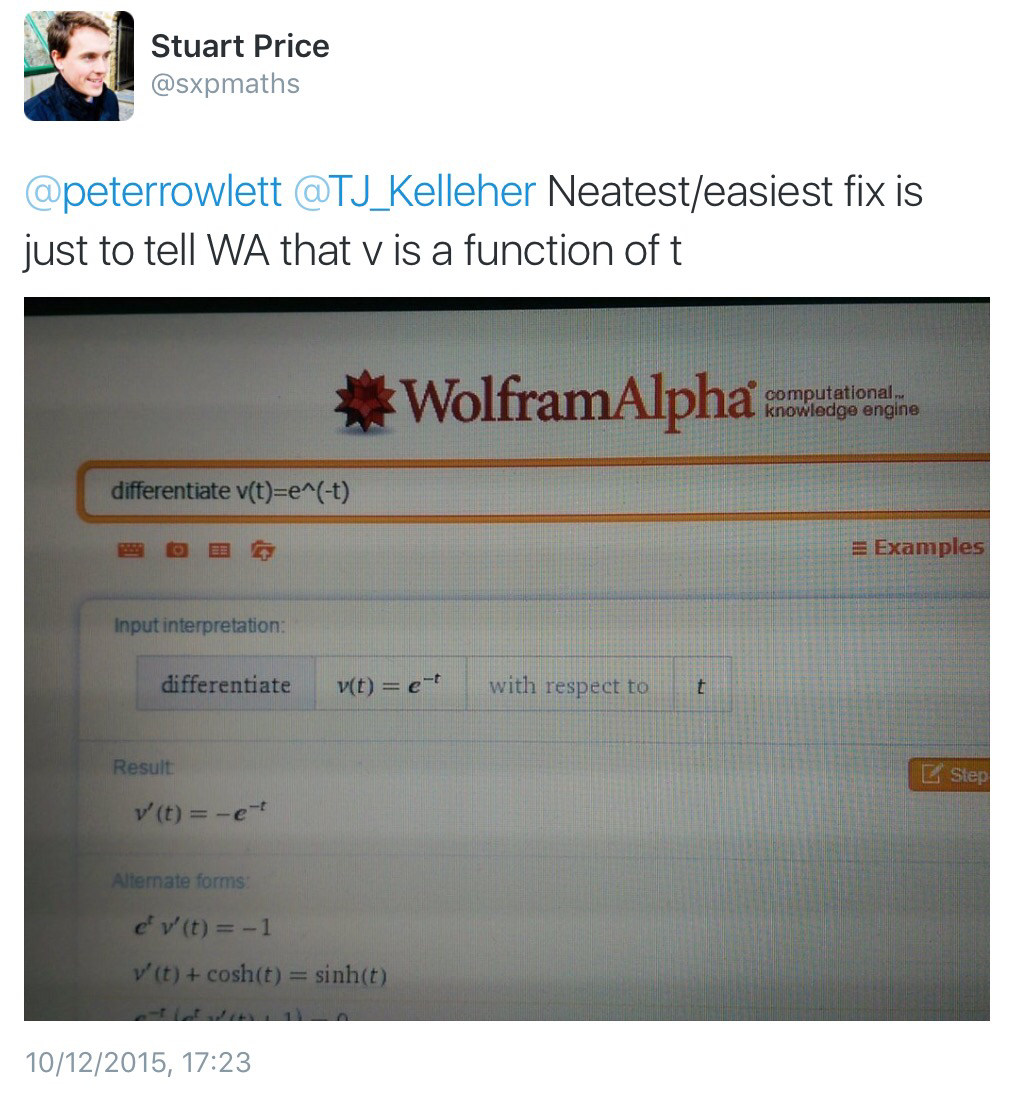
Of course, we understand implicitly that \(v\) is a function of \(t\), but because WolframAlpha doesn’t know this it and differentiates both sides – taking \(v\) to be a constant – and then multiplies by -1 on both sides (removing negative signs if possible is often seen as making an expression simpler). Stuart commented that mking \(v\) a function of \(t\) explicitly solves the problem.
I then commented that I would normally just use the Wolfram Language / Mathematica syntax (D[v[t] = Exp[-t], {t,1}]) – of course this goes against the idea of using free form input but it does remove any ambiguity of what I am interested in WolframAlpha working out.
Ordinarily I use formal syntax almost all of the time when using WolframAlpha as I like the precision that it gives me, however yesterday I discovered that some commands don’t work correctly! for example, if I try to use the DSolve command to solve a second order differential equation with initial conditions I get an error:
whereas just typing the differential equation with initial conditions gives me the solution:
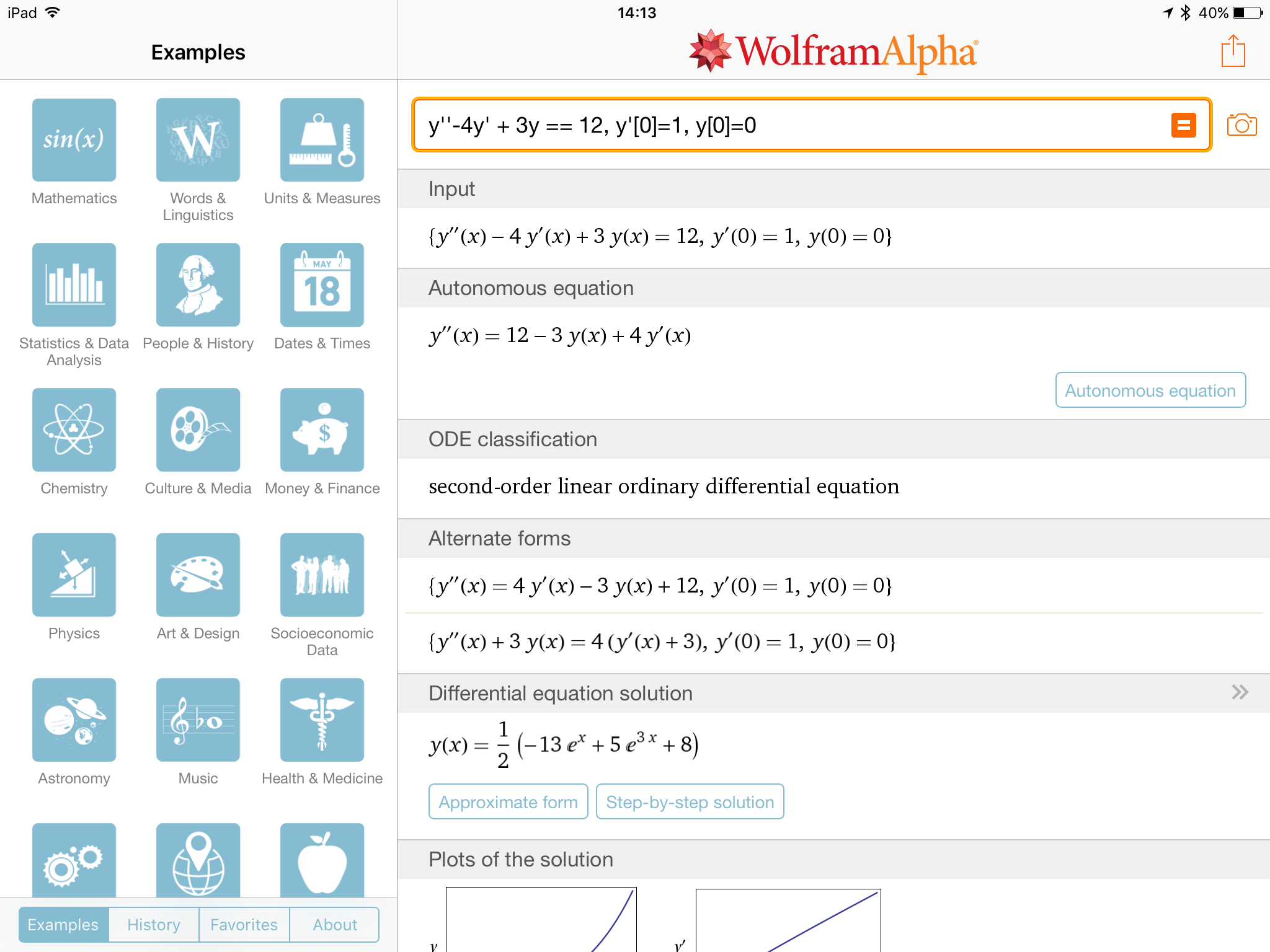
I find this a bit odd – maybe Wolfram are trying to push free form input. Regardless, it is still important to be mathematically precise when entering functions to ensure that you get the correct result.
I’ve recently started using the WolramCloud for computations when I want to use formal syntax and I will blog about that some time soon!