Today one of my colleagues asked me how this followed: 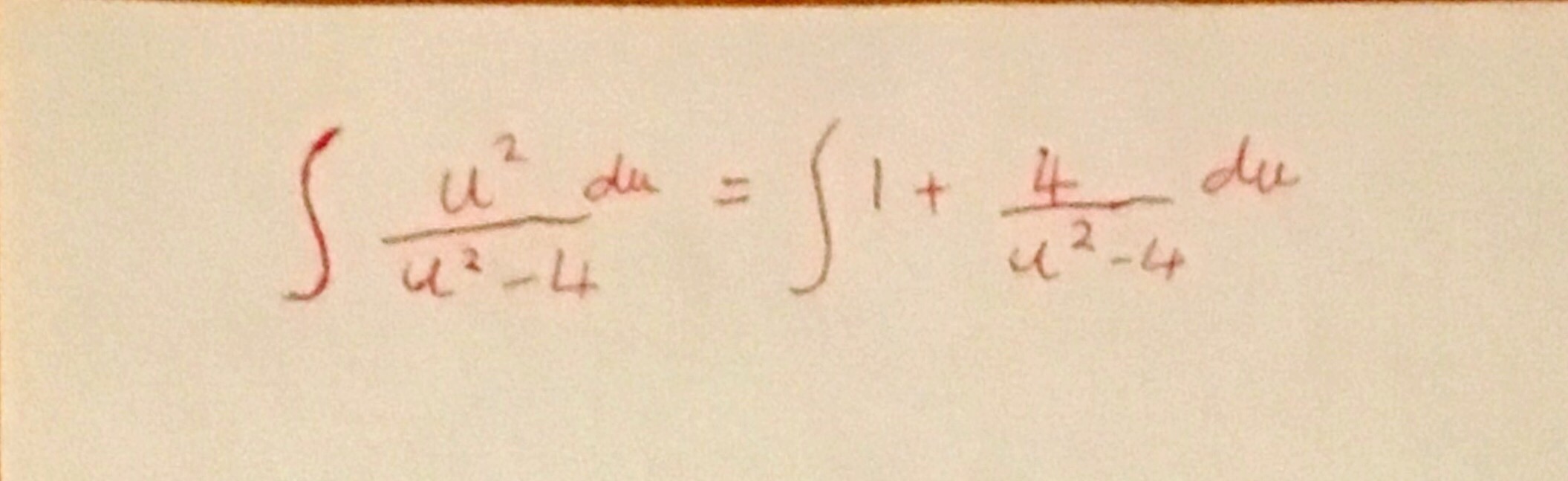 Thinking back my response (in front of the class) was something along the lines of “that’s a fairly standard trick used when integrating”. This troubles me as it makes it seem that it has come out of nowhere by some kind of magical process and probably adds to the feeling that mathematics is a just a collection of rules to be followed.
Thinking back my response (in front of the class) was something along the lines of “that’s a fairly standard trick used when integrating”. This troubles me as it makes it seem that it has come out of nowhere by some kind of magical process and probably adds to the feeling that mathematics is a just a collection of rules to be followed.
A better description, in my mind would be something like the following: “When faced with an integral that you can’t do straight away, try to manipulate it to something that you can do by either ‘adding 0’ or ‘multiplying by 1’. That is you do something that changes the form of the integrand but which leaves it equivalent to what you started with. In this case you ‘add 0’ by adding 4 and then subtracting 4:”
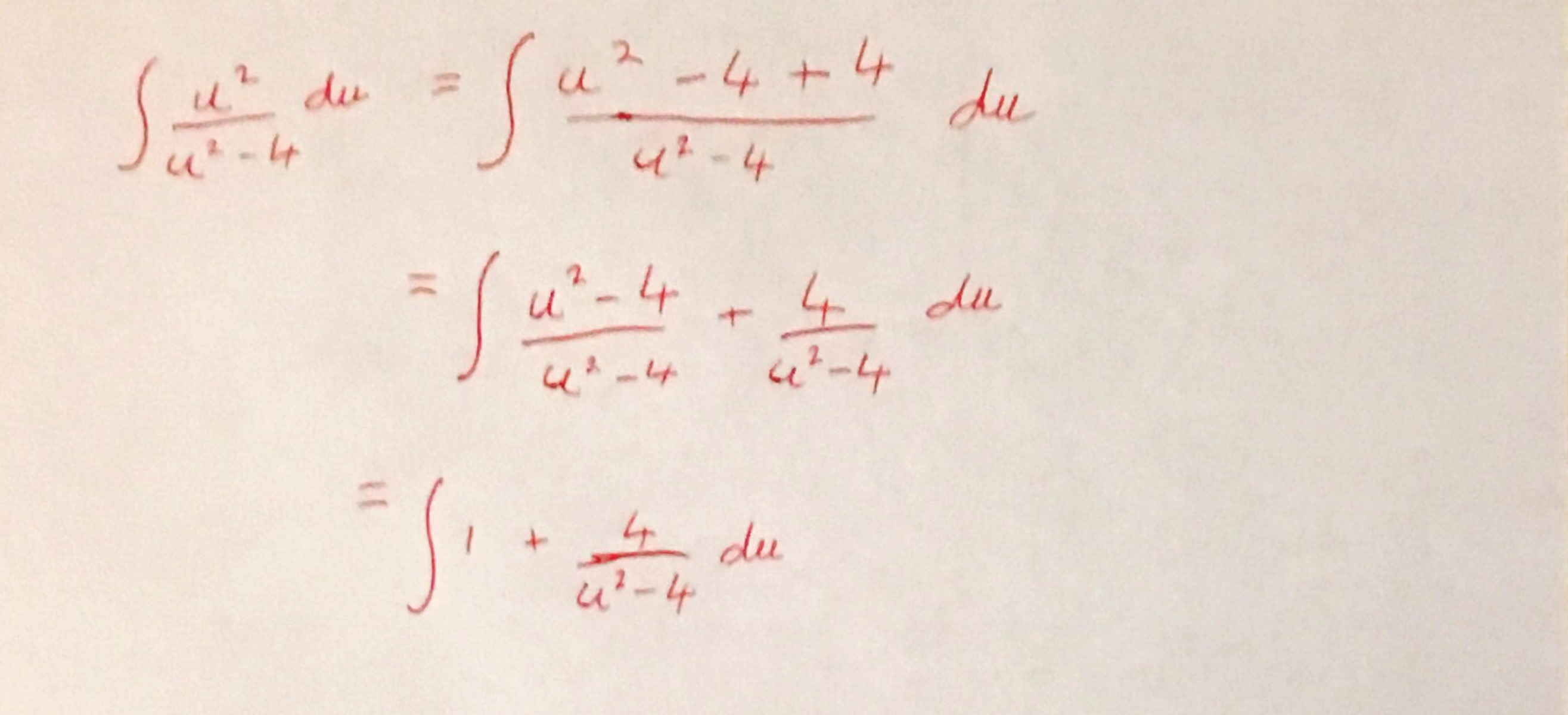 Do you think that avoiding the use of the word “trick” is important?
Do you think that avoiding the use of the word “trick” is important?
In my experience professional mathematicians use this phrase to mean a “commonly used technique” and so it doesn’t have the connotations that the phrase can have.
Should we avoid the phrase? Or try to push for a “maths specific interpretation”?
One reply on “Is “trick” a bad word?”
I sometimes describe myself as a mathematician but really I’m an engineer who teaches maths up to Further A Level and I’ve been doing that for a long time. As a result of the lack of formal maths at university I miss a lot of these ‘tricks’ but all problems are solvable with a sound grasp of the basics. With the above problem there is no need to be aware of the trick, simply re – write as fractions. Similarly I don’t memorise the double angle trig identities but derive them. I encourage pupils to do this too. Understand fully the underlying principles, a thorough understanding of manipulating algebra and be able to deal with fractions effectively means you can achieve success without recourse to memorise common results. This approach permeates through my teaching and I openly discuss it with the pupils.