I’ve just enjoyed reading Anne Watson’s latest blog post “Finding Nemo and Dissection” on the Oxford Education blog and at the end of it was something that I haven’t noticed before.
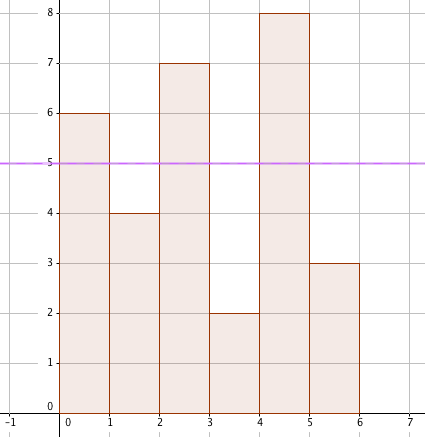
If you represent discrete data as a bar chart, then the arithmetic mean of that data is a number such that if you draw a line at that value on the \(y-\)axis then the area of the bars above the line is the same of the area of the gaps below the line.
For example, consider the data set \(\{6,4,7,2,8,3\}\) which has arithmetic mean \(5\). As you can see from the diagram below the areas above and the gaps below the line (plotted at the arithmetic mean of the data) are equal.