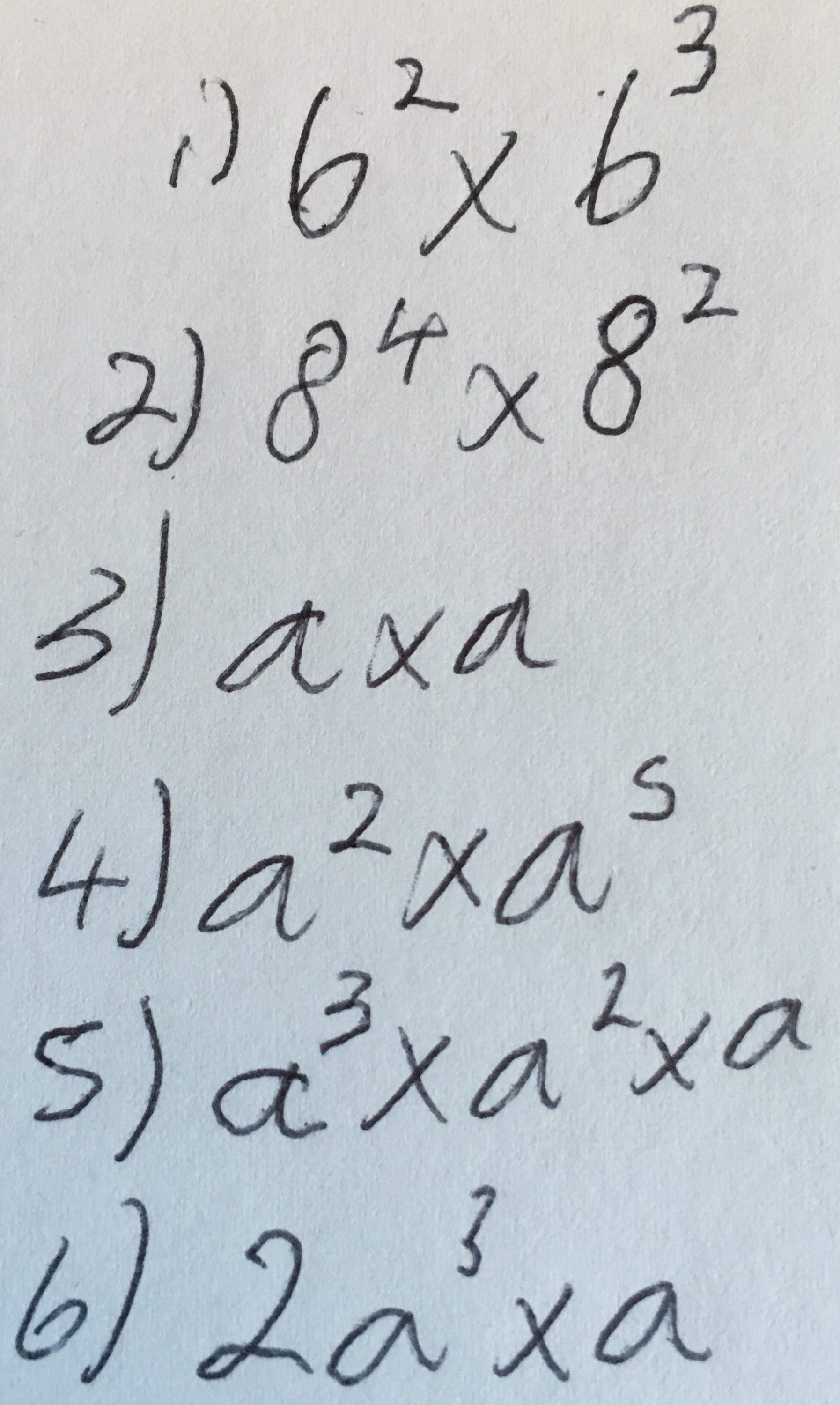Yesterday morning I wasn’t as positive setting off early to #mathsconf5 in Sheffield as I normally am due to having felt really ill on Friday and I still wasn’t feeling great on the Saturday morning. Giving a workshop in the first session meant that not going wasn’t really an option and I was very thankful to @Miss_J_Carter for offering to drive. I’m also going to put not being sure if I recognised Hannah (@MissRadders) in the queue for car park money down to my poorly-ness!
When I arrived I was (incredibly) excited to be given this tea towel by Julia (@tessmaths):
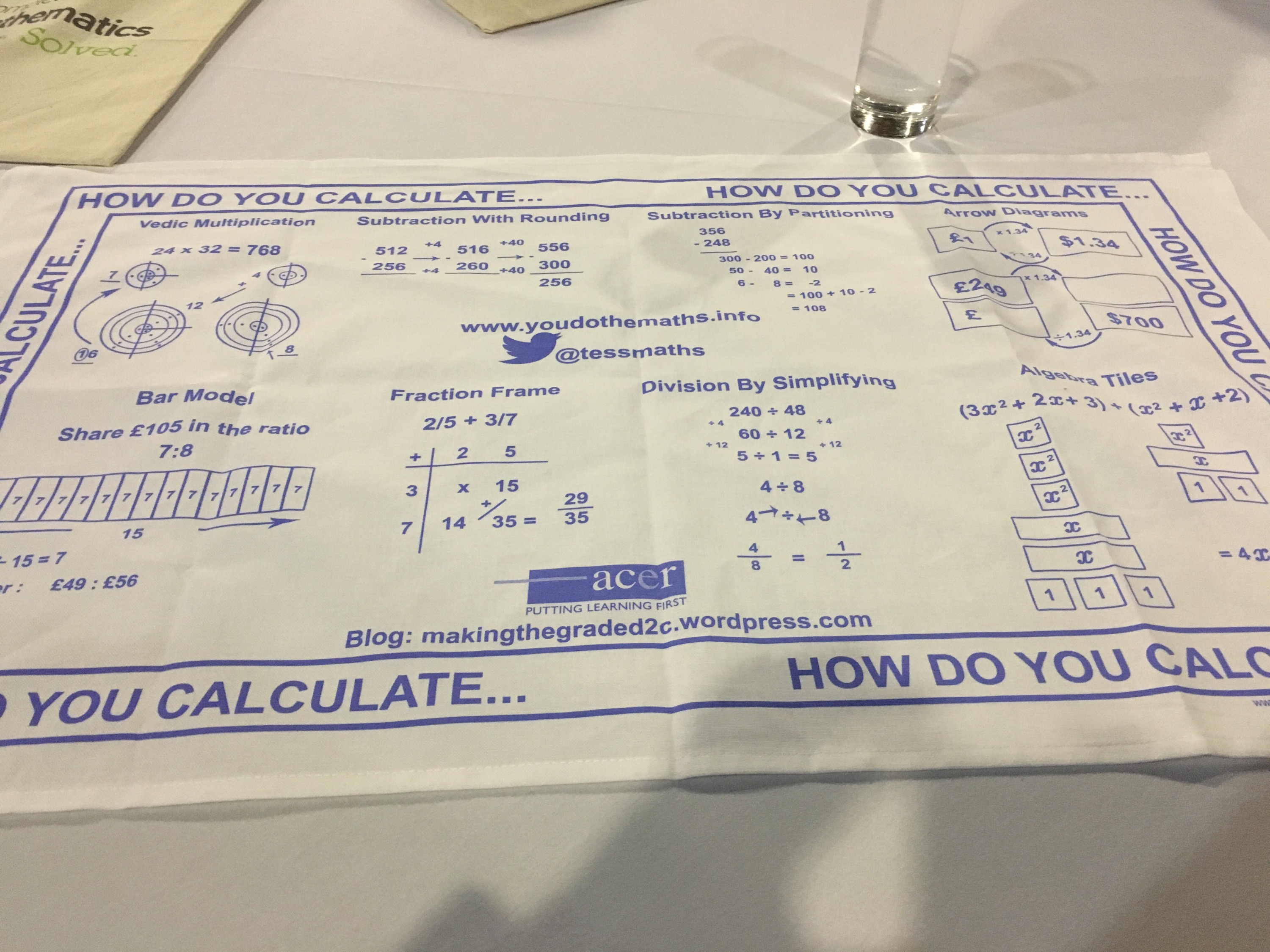
I hope she understands just how happy this tea towel made me!
The conference started as usual with a presentation by Andrew Taylor of @AQAMaths – he helpfully put his slides online here. I was particularly interested to hear about the KS3 assessment materials that they are going to be releasing.
Following that we had the speed dating 🙂 The first one ended up being more of a general chat though. For the second someone who isn’t on Twitter shared the idea of having a grid that students work through to formalise the process of solving an equation for example. I like this idea as it provides a bit of structure and would hopefully lead to better written mathematics from students. The last person I spoke to is also not on Twitter and talked about using tools such as Secretive which I have used a couple of times before but then also mentioned Mentimeter which I haven’t used before. A friend of mine recently mentioned the graphing capabilities of Mentimeter so i need to look at this soon.
I’m going to briefly highlight the best bits of each session, but I didn’t take as good notes as normal so they are definitely not comprehensive!
Session 1:
I was delivering a workshop entitled “How to enjoy (and Succeed at) Your NQT Year” during the first session of the day. I’m not going to say a lot here as I plan to write about it specifically (hopefully tomorrow, definitely by Friday) but I enjoyed the discussions I had with people attending my workshop. It was particularly nice to have @dannytybrown in my session.
[prezi id=”http://prezi.com/-dz30jtfabtw/?utm_campaign=share&utm_medium=copy&rc=ex0share” align=center width=600 lock_to_path=1]
Session 2:
For Session 2 I had chosen @dannytybrown‘s workshop “Time to Slow Down?”. It wasn’t what i was expecting but I really enjoyed it. I was sat on a great table where we had a lively discussion about the initial slide 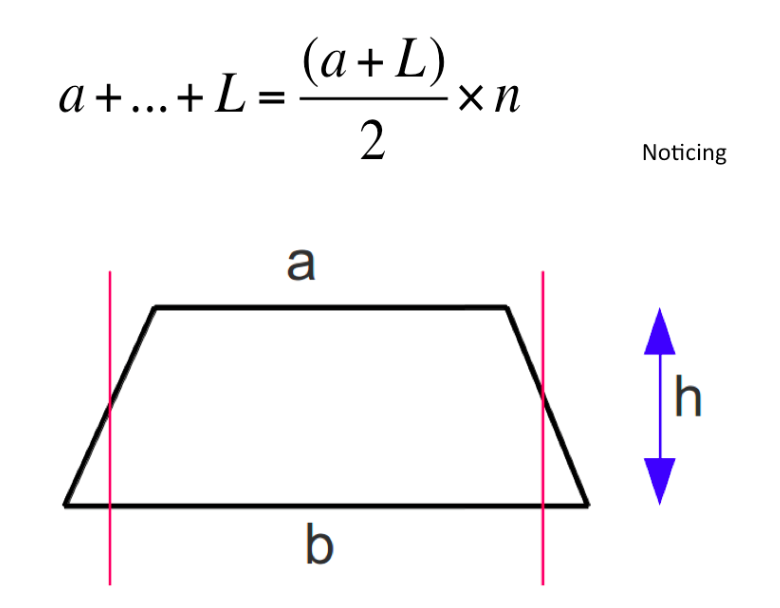
What do you notice? I had never really considered looking at the formula for the sum of an arithmetic sequence in conjunction with a picture of a trapezium before – some great points were made by people in the audience.
We then discussed an account of a conversation between Danny and someone else about an observation of a particular A Level lesson. The conversation is hopefully viewable in these photos of the handout:


It was interesting to consider this as it raises many important questions. I certainly think becoming emotional and letting yourself be annoyed means that as a teacher you don’t reflect properly on a lesson.
Session 3:
Luke Graham (@BetterMaths) chaired a session where attendees collaborated to come up with a list of topics that they are wanting ideas of how to teach in the new GCSE and then some ideas of how to do this. I had been asked to oversee a table looking at the Statistics strand – there really isn’t much in the new GCSE on statistics. The result of this session is shown in Luke’s tweet

I’m looking forward to seeing where he takes this.
The TweetUp:
During a nice long lunch break ( the mini pies were pretty good) the TweetUp organised by Julia (@tessmaths) took place. This is becoming a bit of an institution and I was on the QRCubed table again which embarrassingly I had forgotten how to solve. Lots of people were getting involved with Pete Mattock’s (@MrMattock) STEP questions, Jo’s (@mathsjem) selfie booth and the various other activities on offer. The “TweetUp and do Some Maths” is a great part of the day and if you haven’t been to one before make sure you come at #mathsconf6.
Session 4:
This was the first session that I decided on. Bruno Reddy (@MrReddyMaths), Craig Jeavons (@Craigos87) and Matt Fox (@MFx15) have recently returned from Shanghai and this session “Sh****ai Is Not ADirty Word” was dedicated to them sharing some of the things they experienced and noticed.
I was interested to learn that the students do eye relaxation techniques every day – perhaps something we should implement over here, I’m sure it would help me at least! I think the fact that teachers in Shanghai work in 5 year cycles and must log 240 hours of CPD in those 5 years in order to progress to the next level is significant. This is much more than in the UK and surely improving teacher’s practice is the thing that will lead to the biggest increase in assessment scores (whether we want this to be the focus is another question!).
The quick ramp up in difficulty of the questions concerning the simplification of surds shown on the slide below is very interesting. Question 3 is significantly harder than question 1. 
I would be afraid to use such varied questions (where the difficulty increases quickly) in a “quick response” activity as shown below.
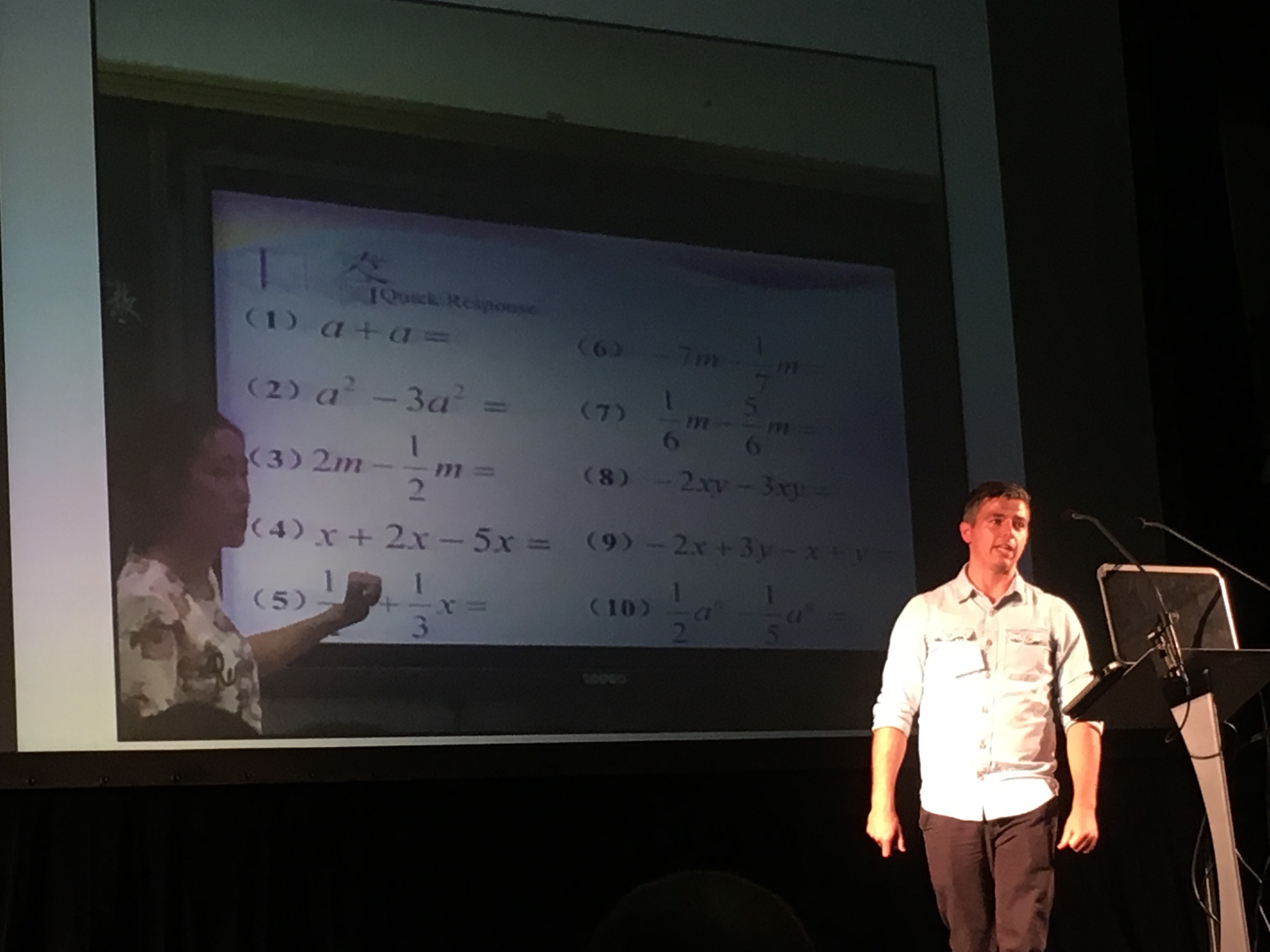 I liked the evidence of students who are equivalent to Year 10 using the \(\because\) and \(\therefore\) symbols to explain their mathematics. I firmly believe that we should be encouraging this sort of formalism in our students, certainly at A-Level.
I liked the evidence of students who are equivalent to Year 10 using the \(\because\) and \(\therefore\) symbols to explain their mathematics. I firmly believe that we should be encouraging this sort of formalism in our students, certainly at A-Level.



The variation in the index law questions above is striking. In the UK we would normally do lots of similar questions such as:
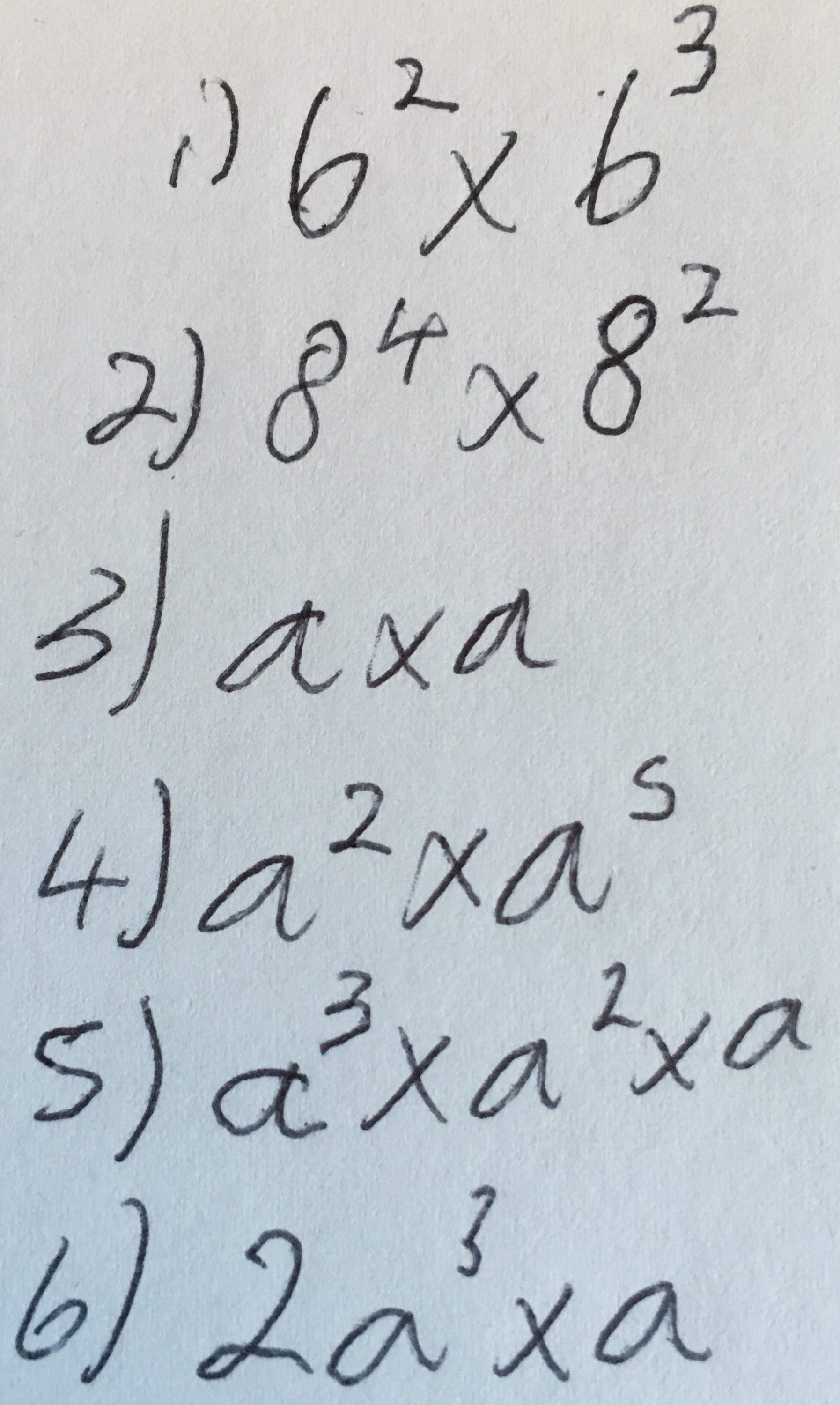 Because of this our students aren’t being exposed to as wide a variety of situations where the index laws can be applied – this leads to difficulties in the future, for example when cancelling algebraic fractions down. James Pearce (@MathsPadJames) has written about this in a great post yesterday.
Because of this our students aren’t being exposed to as wide a variety of situations where the index laws can be applied – this leads to difficulties in the future, for example when cancelling algebraic fractions down. James Pearce (@MathsPadJames) has written about this in a great post yesterday.
Session 5:
Kris Boulton’s (@Kris_Boulton) talk on the “Stories of Maths” had been one that I was really looking forward to and he didn’t disappoint. Writing about it really can’t do it justice and luckily I recorded it, so if you missed it download the file (it’s about 1.6GB) from here and watch it – you won’t be disappointed.
I particularly enjoyed the reading about Sumerian (I think!) shepherds and how they could find out if all sheep had returned before the invention of counting. Will definitely be using that in class. The origin of the word “sine” was also interesting as I didn’t know the full story there.
Overall it was a really good day, and as ever great to catch up with people. Mark McCourt has written a blog post outlining the philosophy of the mathsconfs that is worth a read.
Looking forward to the next one on the 5th March in Peterborough…..
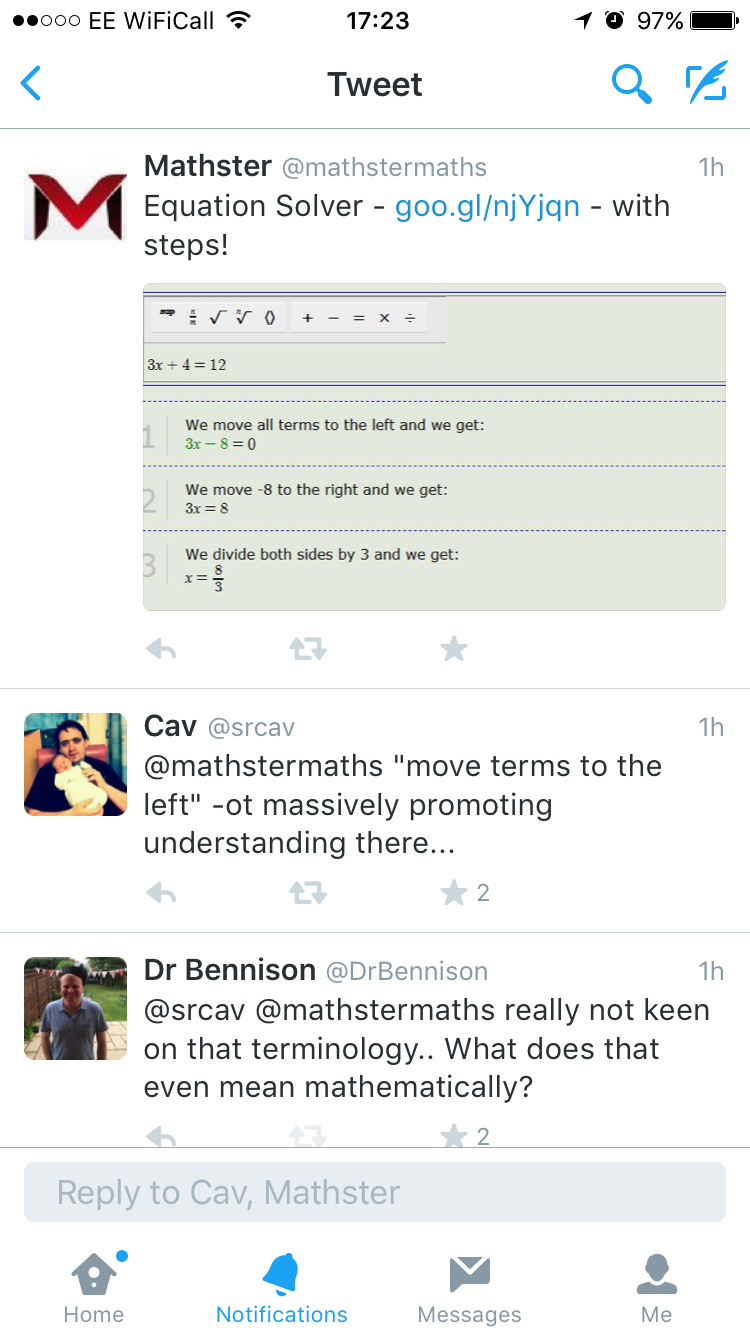
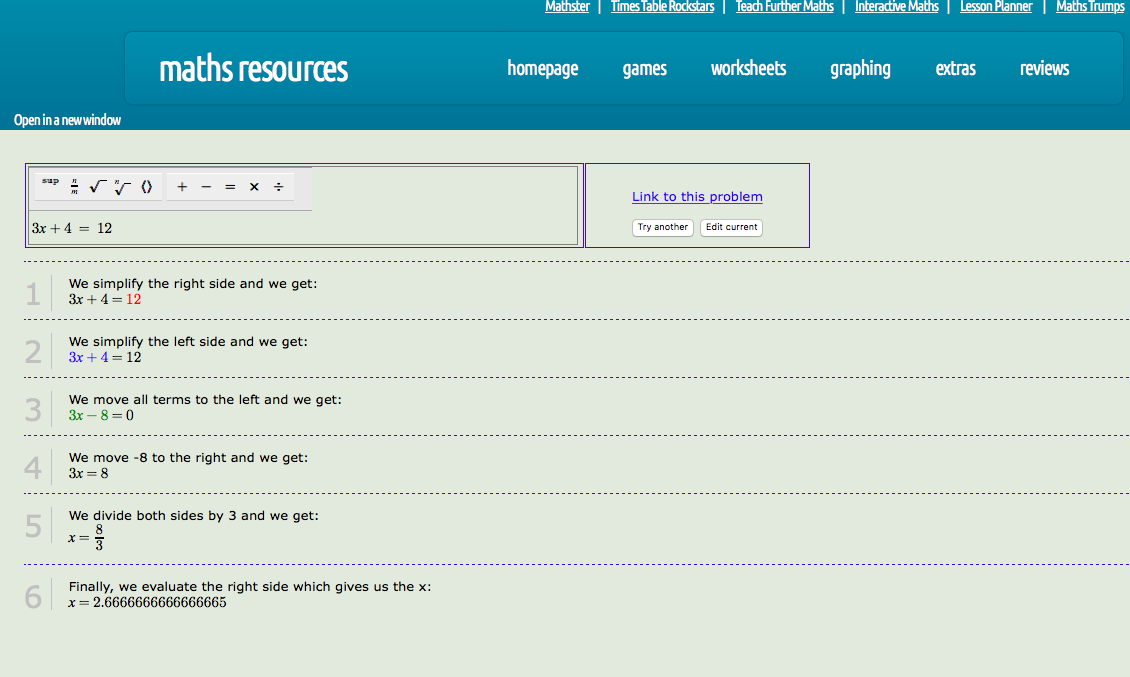
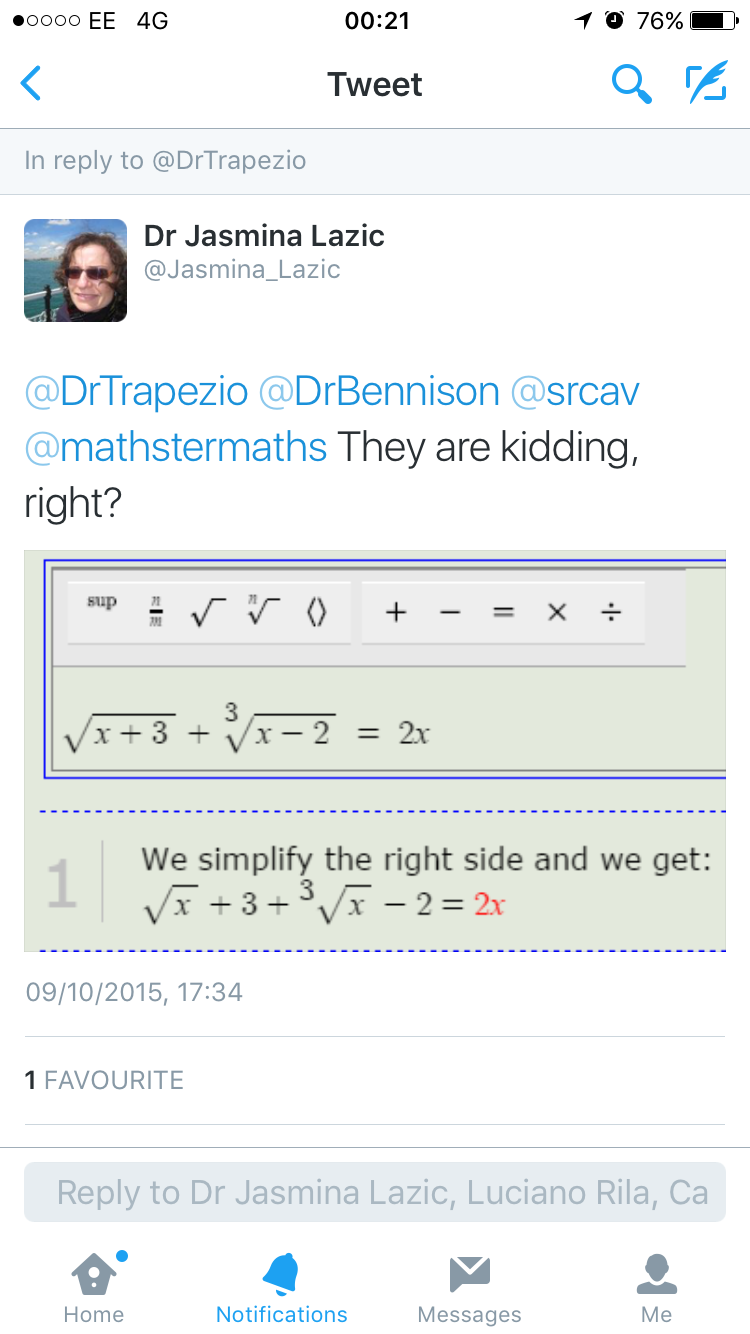 I’m curious as to how this app is working, specifically
I’m curious as to how this app is working, specifically