Last night I read an excellent blog post by Stephen (@srcav) discussing the readiness of students for the current maths A Level. It turns out that this blog post was actually a response to another great post by Jo (@mathsjem) and I was going to comment on both posts, but then thought they would probably be a bit long for comments. So here are some of my thoughts…
The Importance of Algebra
As Jo points out it is possible to do well at GCSE without much of an understanding of algebraic manipulation. Algebra is, in my opinion, the bedrock of A Level, and students need to be able to perform algebraic manipulation correctly, confidently and quickly to do well at GCSE.
This appears to come as quite a shock to many students, who have got used to algebra questions being one of 4 main topics, and normally quite distinct from others. I have only been teaching at school level for a short time, however, to me a diagnostic algebra test at the beginning of Year 12 seems to be a very good predictor of A Level grades (far more so than GCSE grades) if the student doesn’t put work in to practice the algebra skills that they may be potentially lacking.
Timing
The choice of student’s applied modules seems to be important, and to me this choice means that an A Level grade is not really fit for being used by universities to compare students. M1 is a tougher module for a student to complete than either S1 or D1 and so an A Level where M1 and S1 have been chosen isn’t directly comparable to an A Level where the student has “chosen” (or pushed towards by a school looking for improved results) S1 and d!. The new 100% prescribed content of the new A Level should remedy this and enable the students to see maths as the connected subject that it is without the arbitrary distinctions placed on it.
Timing is also a problem for those students who are taking Maths and Further Maths. Ideally, a student could complete all of the standard A Level in Year 12 before studying Further Maths in Year 13. Where this isn’t possible students study Further alongside the standard A Level. Working on FP1 content whilst working on C1 content is obviously problematic as students don’t know all the techniques (polynomial division being one of them) that is expected for the Further Maths content. They also haven’t had the practice, or necessarily developed the mathematical maturity that is expected of them. This has obvious effects on confidence levels of the students, as well as creating time pressures when delivering the content.
Type of Exam Question
As Jo mentioned there is a large change in the wording of exam questions at A Level. I think that there should be greater parity between GCSE and A Level mathematics in this. I understand though, that this may go against some of the GCSE reforms to push questions towards simpler wording and grammatical constructs (as AQA definitely seem to be doing) so that students with weak language skills aren’t at a significant disadvantage in their mathematics exams. If we are taking students onto A Level who have achieved a grade B with less than 50% of the paper correct, it is entirely possible that students with weak language skills will end up taking A Level maths where understanding the exam questions could be problematic.
Students also sometimes find the use of more formal mathematical language and symbols confusing. This could be remedied by introducing some of this into the higher GCSE classes; for example sigma notation could be introduced when computing the mean of a set of numbers.
Managing the Transition
I believe that a mathematics A level is the most rewarding A Level a pupil could take, and so I, like all teachers I’m sure, want to make the transition from GCSE to A Level as manageable as possible.
In my school we set some summer work which is essentially revision of GCSE algebra, though it is clear that not all students have revised this sufficiently when they come to do their initial algebra assessment. This year I also sat the Further Maths students some harder work that was more open ended and of a problem solving nature. I wanted to stretch them and also get an idea of how their brains worked when faced with a challenge. These questions than formed the first lesson of the year. On the whole they were well received by the students with them saying that they enjoyed having a go at them even if they did not correctly solve them. This experience of struggling towards a solution is important. Many Further Mathematics students have probably never struggled with a maths question before and the increase in difficulty can sometimes be uncomfortable and hard for them to handle. Learning to fail and accepting that they will learn an awful lot in the process is an important thing to experience on the road to becoming a mathematician.
I’ve also found encouraging group work important too as this forces them to discuss the maths instead of working in isolation. Being able o discuss the questions and work through problems is important as there often isn’t enough time to talk through problems with all questions in class.
Off Syllabus Mathematics
Last year I was lucky enough to have some timetables time to work with the most gifted of the year 11 students, looking at mathematics that wasn’t on either the A Level or GCSE Syllabi. Due to my interests we looked at, among other things, floating point representation of numbers and round off errors, formulae for calculating Pi and iterative schemes for solving linear systems. Many of these topics are typically studied in Year 2 of an undergraduate degree, yet they were accessible to students who had just completed a GCSE course (of course some of the rigorous analysis was left out….). I am passionate about exposing students to maths outside of the syllabus as I think background knowledge often helps them see how to approach a question in a different light, or at the very least provides a motivation for studying what we do at school which is sometimes not explained enough.
A Final Niggle
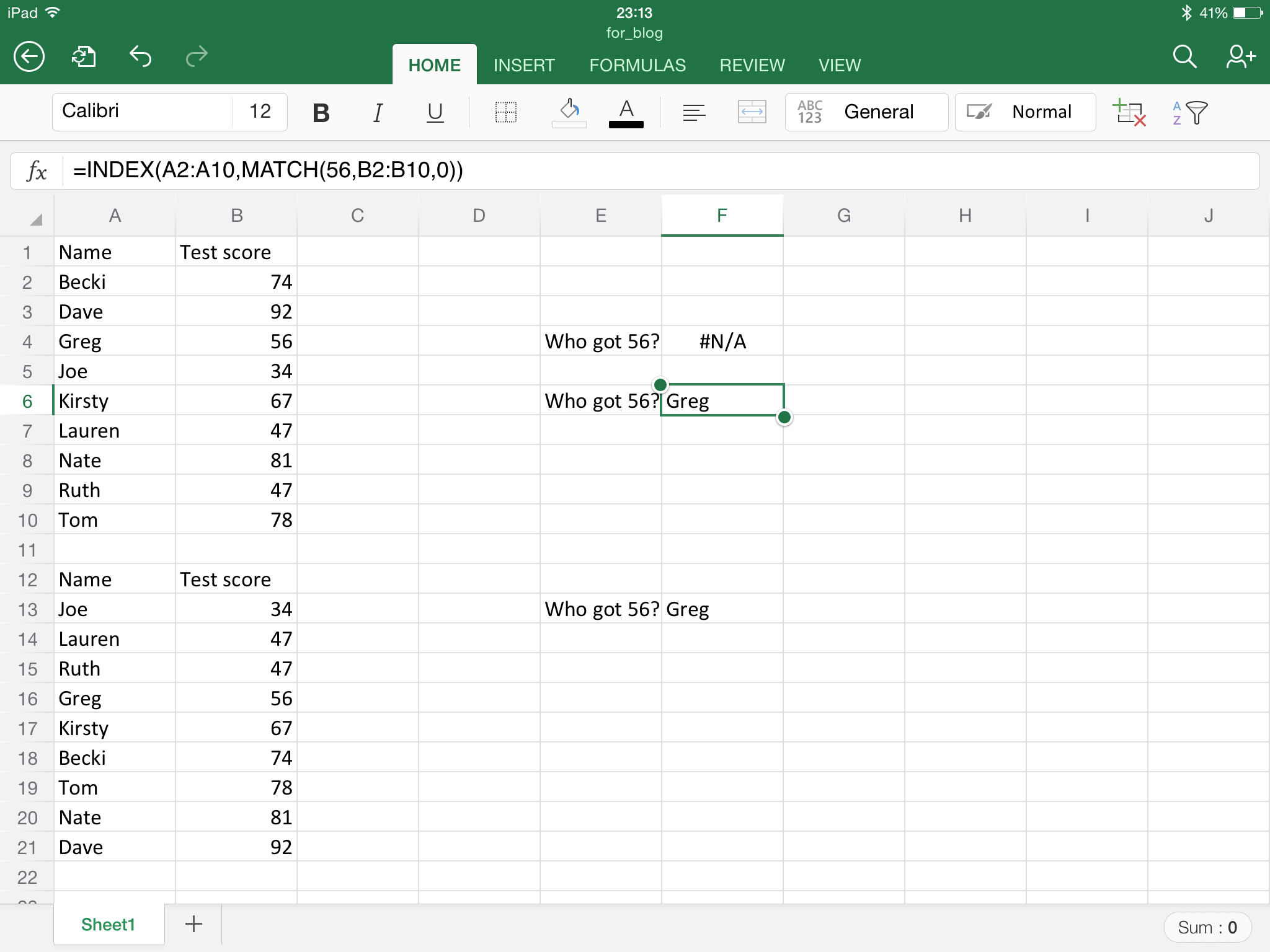
One thing that I have always loved about maths is the “universal truth” that maths brings. A mathematical concept is always true no matter what, and something that you learn early on cannot be then shown to be rubbish. This is in contrast to the other sciences, for example in Chemistry when you learn about chemical bonding you seem to be forever told to forget what you have been told previously! For this reason it always pains me when teaching the quadratic formula that students begin to believe that getting a negative discriminant must mean they have gone wrong! I can’t see any reaso. Why a higher tier GCSE student couldn’t handle a question such as the following:
I certainly don’t understand why complex numbers are not in the standard A Level as they are so fundamental.
Anyway, I’m looking forward to joining in with Jo’s chat tomorrow and looking forward to hearing other people’s views.