This Saturday I went to a great session organised by the East Midland’s branch of the Association of Teachers of Mathematics. It was led by Colin Foster of The University of Nottingham who was talking about “Rich Mahematics from Closed Questions”.
Writing about the session in a no-linear fashion I liked how he used Fermat’s Last Theorem as an example of a yes-no question (often seen as a closed question) leading to rich mathematics.

A closed question is often defined as a question with one correct answer and no scope for discussion. The open vs closed question idea is something that is discussed often, with closed questions being seen as inferior to openquestions and not readily leading to rich mathematics. The aim of this session was to show that rich mathematics can come out of closed questions.
I liked the initial question of \( 15 \times 823 \). This works out to be 12345. I think this could be a nice launch point for a lesson, looking at other similar sums, divisibility rules etc.
Colin then made the point that two closed questions together or a sequence of closed questions can be a good prompt to some interesting maths. He first gave two quadratics \(x^2+7x+6\) and \(2x^2+7x+6\); both of these quadratics can factorise. Then the prompt questions could be things like “Is this a fluke?”, “What can we say about how to make these?”. I confess I haven’t figured this out yet, so will probably write about it when I do.
As an example of a sequence of questions consider the following:
- How many factors does 10 have?
- How many factors does 100 have?
- How many factors does 1000 have?
- How many factors does 10000 have?
I started by manually listing factors, and soon noticed a pattern of the square numbers appearing. It becomes much clearer when you realise that \(10 = 2 \times 5 \), \(100 = (2 \times 5)^2 = 2^2 \times 5^2 \), \( 1000 = 2^3 \times 5^3 \) and so the factors can be computed using a two-way table
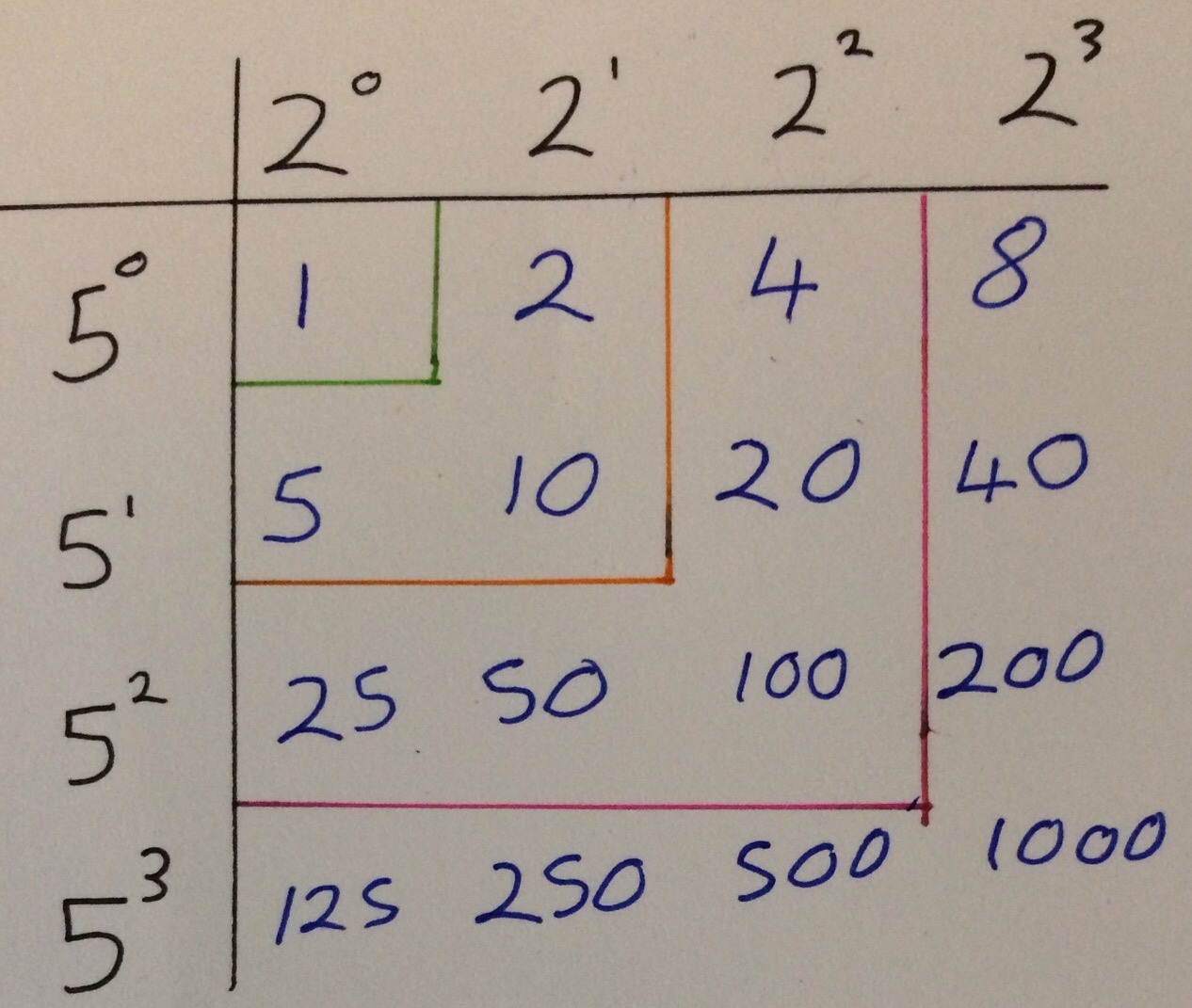
There are many opportunities for students with this task including practise at finding factors, spotting number patterns, predicting future terms of the sequence, generating nth term rules and investigating how the factors of other sequences grow (for example 6,60,160,1600 and 2,4,8,16,32). Of course not everyone in the class will reach the same point, but this isn’t a problem. I really liked Colin’s justification for doing these kind of activities:
“The emphasis is on the thinking going on in the classroom, not on the kids getting to the final answer”
This is a nice “low floor, high ceiling” task and I’m going to use it for an observed lesson later this week, and I will blog about the lesson in full towards the end of the week.
I also realised (something that in hindsight I should have known before as it is obvious) that any prime number to the the power of \( n \) has \( n+1 \) factors.
After looking at factors, Colin presented some inequalities to shade (see his paper here for more information – it’s a nice short article!) and a few problems about fitting rectangles into squares.
All in all it was a great session (it was also good to catch up briefly with Rob who is the secretary of the East Midlands Branch) and the £5 cost is a bargain.
It also reinforced the fact that I have always been irritated by the open/closed questioning distinction. An open question can just as much lead to narrow mathematics as a closed question – it’s the questioner (is that a word?!) that is important.