Almost a couple of weeks ago now (I can’t find the original tweet) John McCormack (@JohnJMcCormack) tweeted to me this “bumping” method for subtraction.
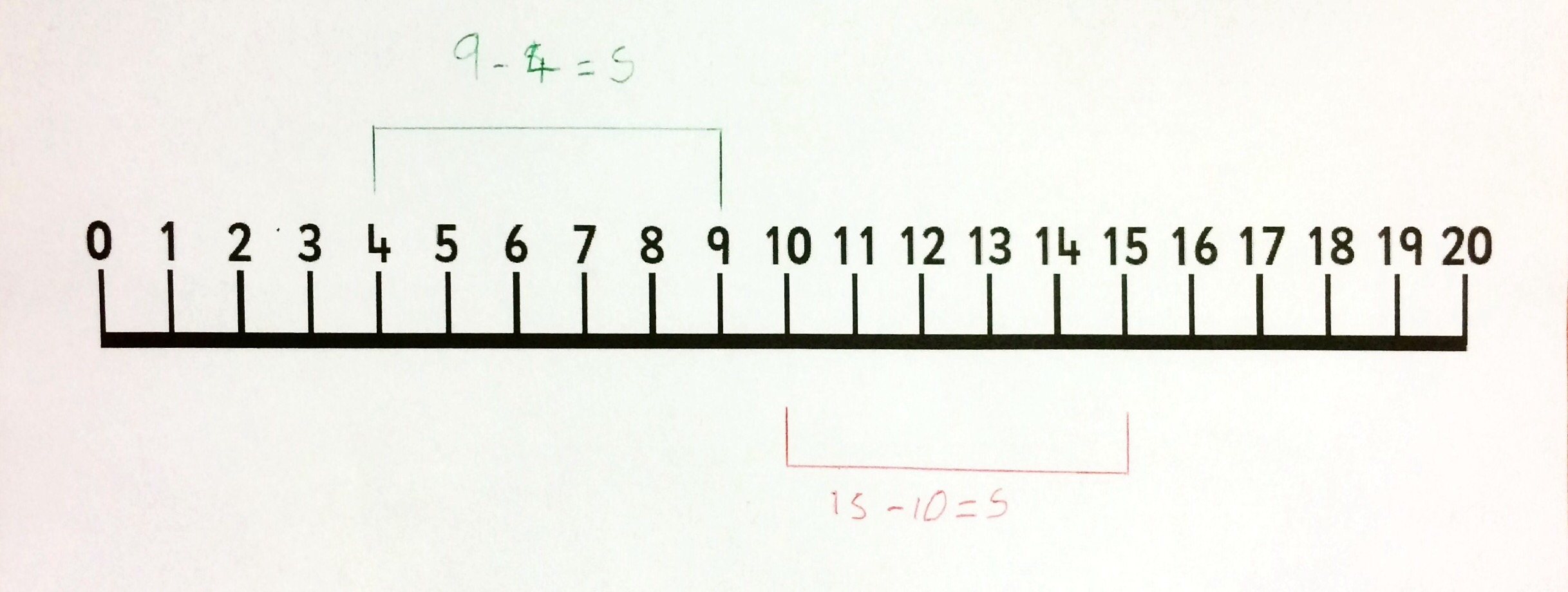
I haven’t seen this method promoted before. It makes use of the fact that the difference between 9 and 4 say is the same as the difference between 15 and 10:
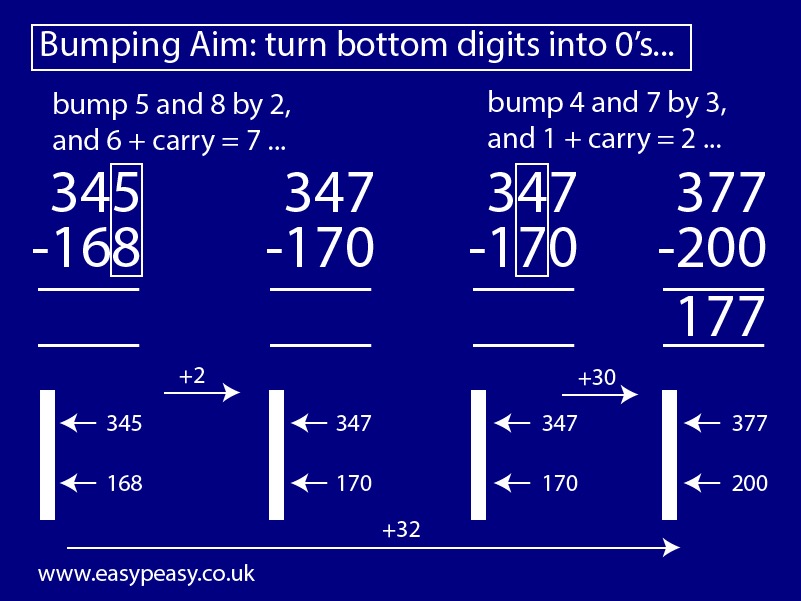
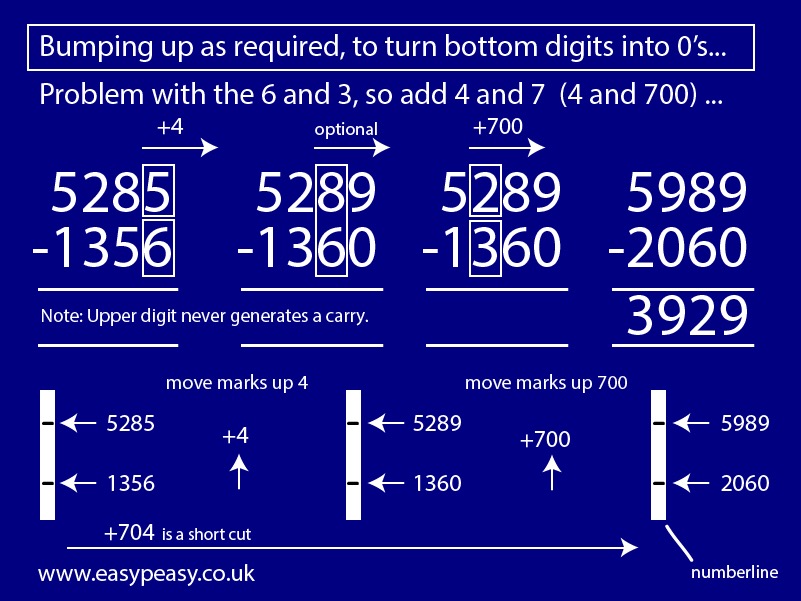
Subtracting a number ending in zeros is clearly easier than subtracting a general number from another and this is the inspiration for the bumping method. This is something that I (and probably a lot of people who have a good number sense) do when performing mental calculations, but I wouldn’t have thought to do it as written method. The only difficulty is remembering of the carry.
Here’s another example:
John has a website where he has posted some black and white examples.
I’d be really interested to hear what you think of this method – I quite like it, but I’m not sure I’d want to teach it as the general method for subtraction.
Would you teach this method and why? Do you have any examples where you think this will be helpful or where it won’t work?
2 replies on “The Bumping Method”
Hi Tom, this is indeed a lovely alternative to the standard algorithm worth treating as enrichment for those who’ve mastered the standard approach. I agree wholeheartedly with your caution about teaching it as standard. (And I’ll go on a bit about this…) Beware the law of unintended consequences and the impulse to teach novelty as if that meant “better”.
This variant, and many others, have been considered, weighed, and tried against the standard algorithm in more contexts that you care to imagine and have been known since before the time of Leonardo of Pisa who introduced Hindu/Arab arithmetic to the West 1000 years ago. And the standard approach has prevailed (yes, more-or-less worldwide, with only minor variants). Leonardo himself tried many of the variants. E.G., for a while he favoured lattice multiplication but in the end rejected it as burdensome and poorly organized. Some present these things as if they were new; actually they are as old as the hills.
Mathematics is a discipline full of standard practices and presentation conventions, and novel approaches can train students to be left-handers in a world of right-handed scissors (cognitively, I mean). If standards mean nothing, then why not write numbers backwards — say 124.76 means sixty-seven and four hundred twenty-one thousandths? Are they not equivalent ways of doing things? Imagine the consequences if half the students were taught this. There’s an old joke in the UK that the government is planning to switch the law so everyone drives on the right side of the road, but they’re going to introduce it slowly. First the lorries will change over…
The urge for educators to reinvent the processes, notations and nomenclature of a discipline invented and refined over centuries by the smartest people in history is hubris. That is even before one takes into account that for our best and brightest going into STEM disciplines, standards will be essential — for them mathematics is a precise language in which what one person writes down is critical for another to understand, immediately, clearly and without ambiguity. The simplest calculation or communication error can lead to disaster (examples abound). In Engineering there is a saying with a lot of truth to it: If you make an error — somebody is going to die. Why would an educator in grade 3 think, “Hey, it’s a good idea to scramble the way my students do this standard thing; it will look really cool and different, and they’ll be, like, always speak math in an exotic, foreign-sounding accent!” Our world is moving rapidly into higher levels science and technology, so those affecting millions of others’ lives must be more and more conversant in extremely abstract language (i.e., mathematics) of what value is it to introduce confusion and ambiguity concerning what students write down to record their work in that language?
This is a fantastic comment. Thanks Robert 😉