The Arithmetic Mean – Geometric Mean (AM-GM) inequality is possibly one of my favourite inequalities (another is the Cauchy-Schwarz inequality, see a later #summerblogchallenge post for more details on this).
Earlier this week I was honoured to have received an envelope of goodies from Ed (@solvemymaths). Alongside the very cool mathematical Mr Men stickers, there was a note from Ed with a lovely geometric illustration of the AM-GM for two lengths \(a,b\).
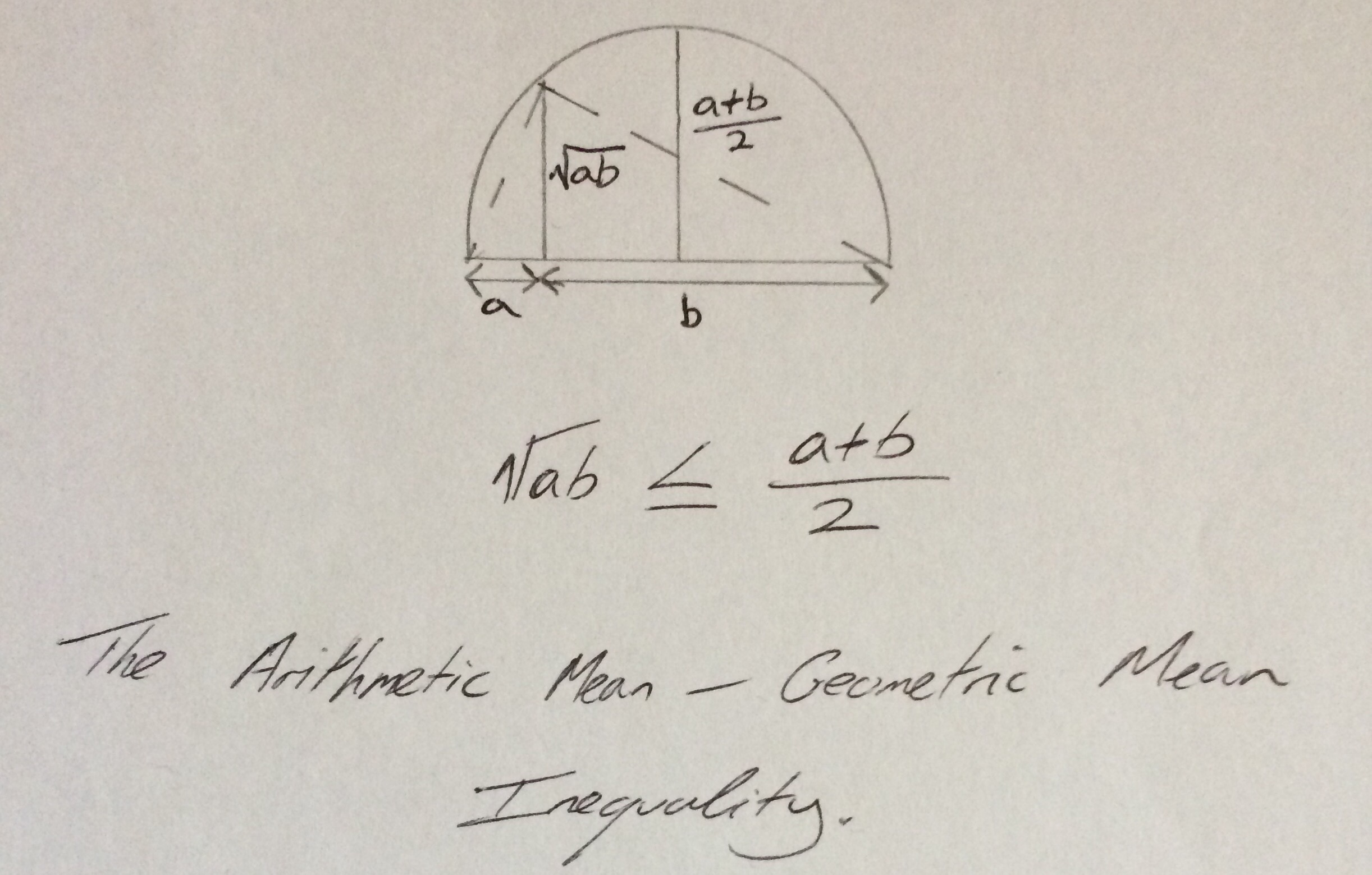 In words, the AM-GM inequality states that the arithmetic mean of a set of (non-negative) numbers is always greater than or equal to the geometric mean of the set of numbers. More formally, the AM-GM inequality can be stated as follows: For a set of non-negative real numbers \(a_1,a_2,a_3,…,a_n\) the following inequality holds
In words, the AM-GM inequality states that the arithmetic mean of a set of (non-negative) numbers is always greater than or equal to the geometric mean of the set of numbers. More formally, the AM-GM inequality can be stated as follows: For a set of non-negative real numbers \(a_1,a_2,a_3,…,a_n\) the following inequality holds
\(\frac{a_{1}+a_{2}+a_{3}+ \cdots + a_{n}}{n} \geq \sqrt[n]{a_{1}a_{2}a_{3} \cdots a_{n}} \)
Example: For the set \(1,6,9,15\) the arithmetic mean is \(\frac{31}{4} = 7.75\) and the geometric mean is \(\sqrt[4]{810} \approx 5.3348 [\latex].
Proof: There are many different proofs of the AM-GM inequality. The excellent Art of Problem Solving website lists a few here . I particularly like the one using the rearrangement inequality as it is so concise.
The AM-GM inequality is often useful for questions on STEP and Maths Challenge papers, here is a typical question and a solution.
Question: Given that [latex]a,b,c\) are non-negative integers, show that
\((a+b)(b+c)(a+c) \geq 8abc\)
Solution: Given that \(a,b\) then applying the AM-GM inequality we have that
\(\begin{align} \frac{a+b}{2} &\geq \sqrt{ab} \\ a+b &\geq 2\sqrt{ab} \end{align} \)
Performing similar calculations with the other pairings we can obtain
\( \begin{align} b + c &\geq 2\sqrt{bc} \\ a+c &\geq \sqrt{ac} \end{align} \)
So, since the numbers involved are all positive we can multiply the inequalities to obtain
\( \begin{align} (a+b)(b+c)(a+c) &\geq 2\sqrt{ab}2\sqrt{bc}2\sqrt{ac} \\ &= 8\sqrt{abbcac} \\ &= 8\sqrt{a^2b^2c^2} \\ &=8abc \end{align} \)
as desired.
Can you come up with a nicer solution? Can you come up with similar questions?
The AM-GM inequality comes up in higher level maths too, a friend, Edward Hall of the University of Leicester has reminded me that it is used in a modified form when proving the continuous stability of the solutions to parabolic PDEs. He also mentioned that he has recently seen it used in a paper concerning Discontinuous Galerkin (more on these in the future) methods for quasilinear PDEs.