At the beginning of July Stuart Price (@sxpmaths) blogged this post looking at A Level textbooks through the ages. I really enjoyed reading this, and was particularly drawn to a picture of a book that described computer programs written in Basic for use in the maths classroom. I was so keen to look at this that I straight away ordered a copy from Amazon and here it is:

This book is fantastic, and it’s a shame that I don’t know of anything similar today (does anyone reading this?) – cue for me to write one, yet another project….
The BBC Micro holds a special place in my heart as it is the first computer that I can remember using at Grove Primary School. I remember sitting at one in the BBC room and doing various things, including my first bit of programming in BASIC (I later had a fairly long hiatus before coming back to coding).
Having become used to modern computers you forget the limitations of older computers such as the BBC Micro. For example, at the beginning of the book some of these limitations are mentioned, such as the fact that the BBC Micro’s filing system can only cope with 31 filenames. I particularly like this quote from the introduction to the book
“The lack of ‘idiot-proofing’ means that they [the programs] may sometimes ‘crash’, but in these circumstances a consideration of why it went wrong may itself be very illuminating, This will usually be due to inaccuracies in computer floating-point arithmetic, the non-existence of solutions, or the singularities of functions, all of which children should be aware of.
I don’t know of many ‘children’ who have an understanding of floating-point arithmetic or the failure of certain numerical methods in the presence of singularities – it is even possible to get through some undergraduate numerics courses without really tackling these issues!
I am going to write a few posts over the summer looking at some of the programs in this book, with the odd modification (I’ve quite enjoyed doing a bit of Basic for the first time in over 20 years).
Of course, to run some BBC Basic programs I either need access to BBC Micro (If anyone has a working one that they don’t want anymore please let me know!!) or a decent emulator. As a mac user there aren’t many BBC emulators available, and those that are don’t seem to have been maintained since 2012. But then I found this excellent Javascript emulator by Matt Godbolt (@mattgodbolt). On his blog there is a lot more detail about the implementation of the emulator, as well as some other cool posts – I urge you to check them out if you are interested in coding! The video about the BBC emulator is definitely worth a watch. It’s sad that the emulator doesn’t apper to work on an iPad though.
I first tried Program 1 from the book, which is a simple program to compute the first \(n\) triangke numbers, where \(n\) is an input from the user. This is shown on the screen shot below:
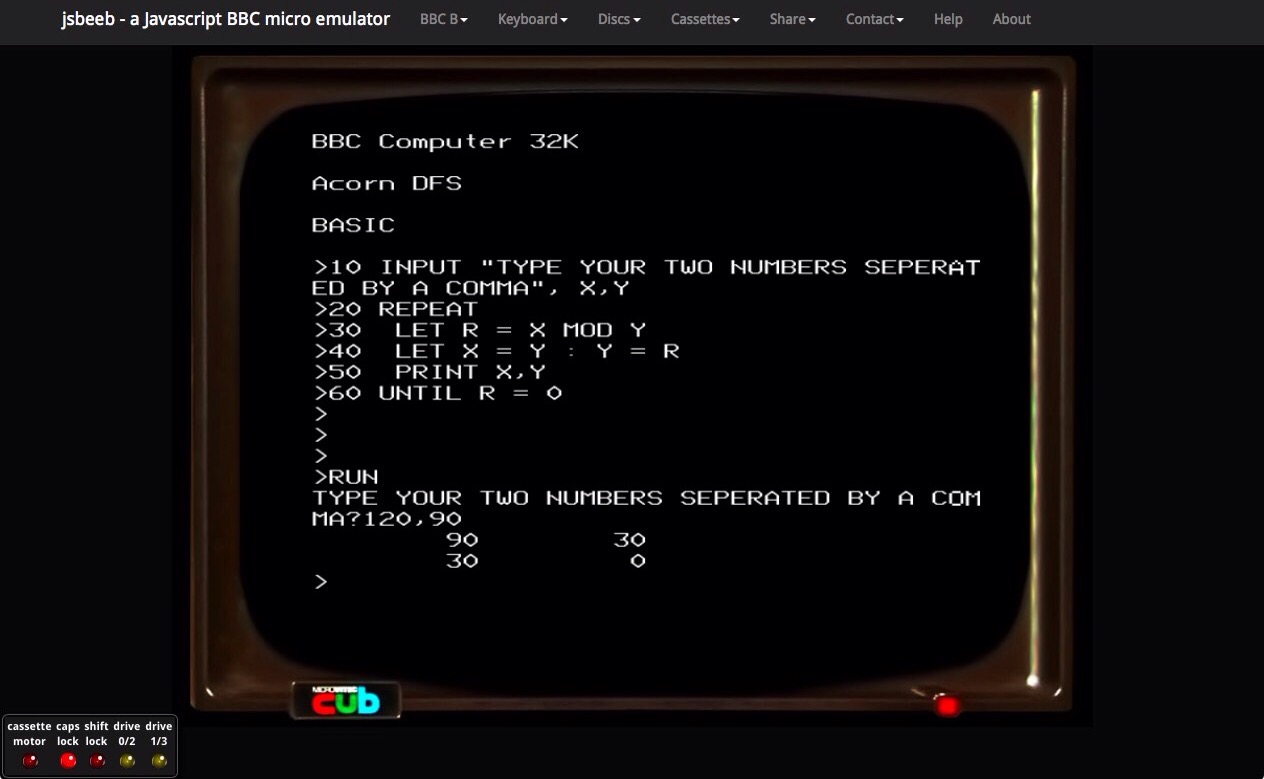
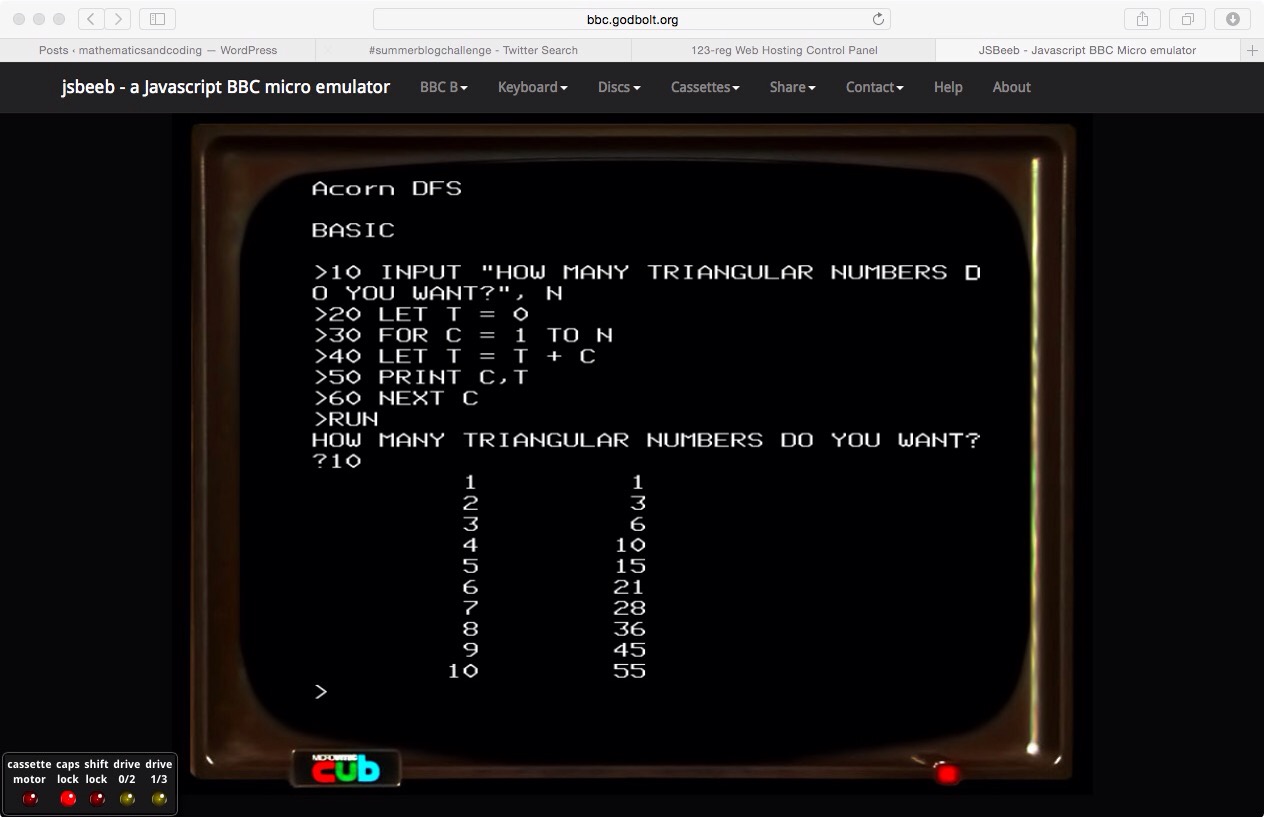 I then thought I would try the highest common factor program:
I then thought I would try the highest common factor program:
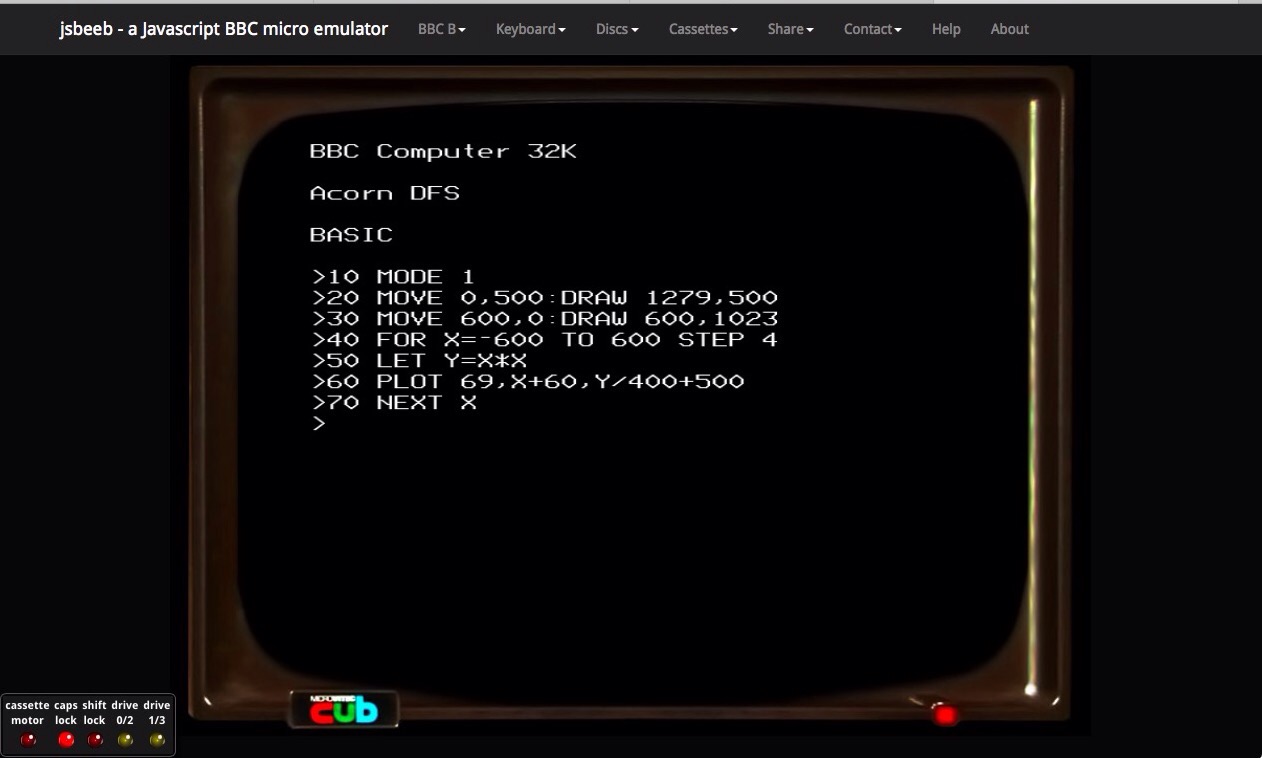
 I then thought I would look at something a bit more complicated, and try plotting the graph of \( y = x^2 \). One thing that you don’t have to do with things like scaling the output explicitly to fit the graph onto the display when using Matlab or NumPy. Of course the BBC Micro and BBC Basic is not as sophisticated as this, and we are explicitly giving coordinates on the screen of where to colour a pixel – because of this osome scaling needs to be done. This explains the divide by a 400 on line 60 of the below code from the book.
I then thought I would look at something a bit more complicated, and try plotting the graph of \( y = x^2 \). One thing that you don’t have to do with things like scaling the output explicitly to fit the graph onto the display when using Matlab or NumPy. Of course the BBC Micro and BBC Basic is not as sophisticated as this, and we are explicitly giving coordinates on the screen of where to colour a pixel – because of this osome scaling needs to be done. This explains the divide by a 400 on line 60 of the below code from the book.
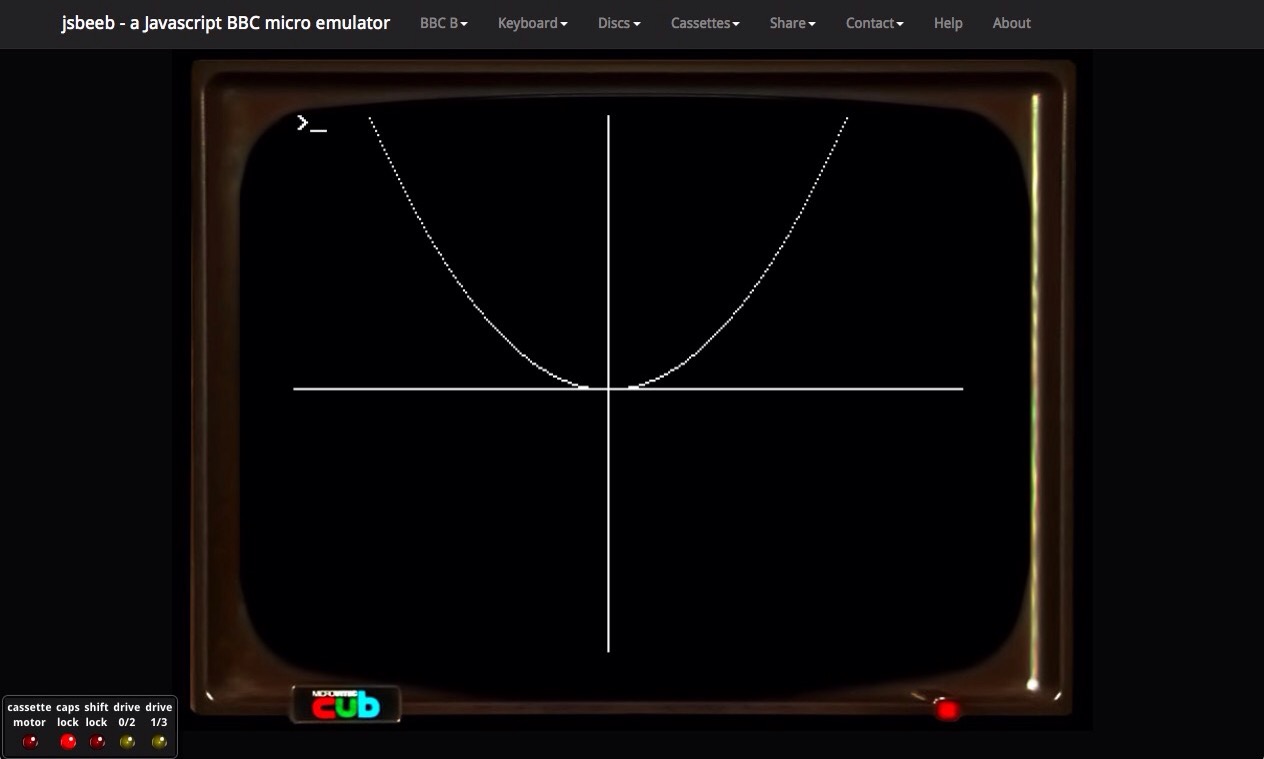
 This code generates the following output which is recognisably the curve of \(y=x^2\)
This code generates the following output which is recognisably the curve of \(y=x^2\)
 I’m going to play a bit more with the graphics commands and will post next week with some further programs from this book, and maybe one that I have written myself too.
I’m going to play a bit more with the graphics commands and will post next week with some further programs from this book, and maybe one that I have written myself too.
3 replies on “The Magic of the Micro: Part 1”
I love today’s post 🙂 ps I’ve always played with the idea of writing s text book too just for fun….
I’m also interested in the intersection of learning math and programming. I have not seen a good entry-level math-focused language for students (e.g. Scratch is great for animation but not so much for math), so I tried my hand at writing one: http://www.mathgram.com. I’ve had mixed success with it with my homeschooled son, but I need help to learn where it could be successful. I’d love if you could take a look and let me know your thoughts on how/where it could be useful.
Sorry for the late reply. Thanks for the comment – mathgram looks interesting.Could you DM me an email on Twitter please?