Yeaterday I picked up my free copy of The Times with my My Waitrose Card and on page 3 it had this puzzle:
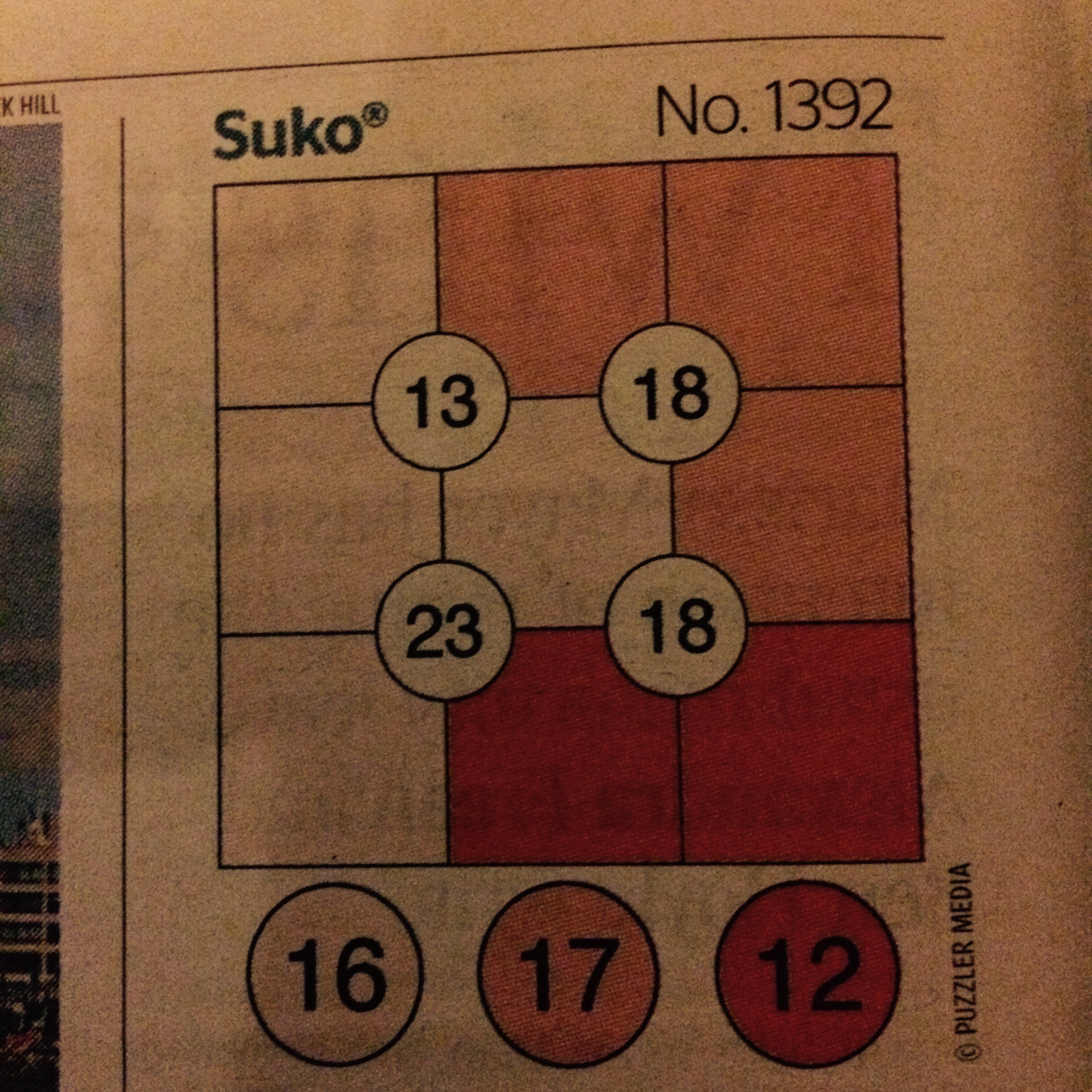 The rules are deceptively simple
The rules are deceptively simple
- You must place the numbers 1-9 in the 9 squares, using each number only once.
- The number in each circle should be equal to the sum of the four surrounding squares.
- Each colour sum is correct.
This puzzle turns out to be trickier than it looks, and this was the intention according to this little bit of history. The puzzle was created by Jai Gomer of Kobayaashi Studios.
The three pictures below show my workings to solve this puzzle.
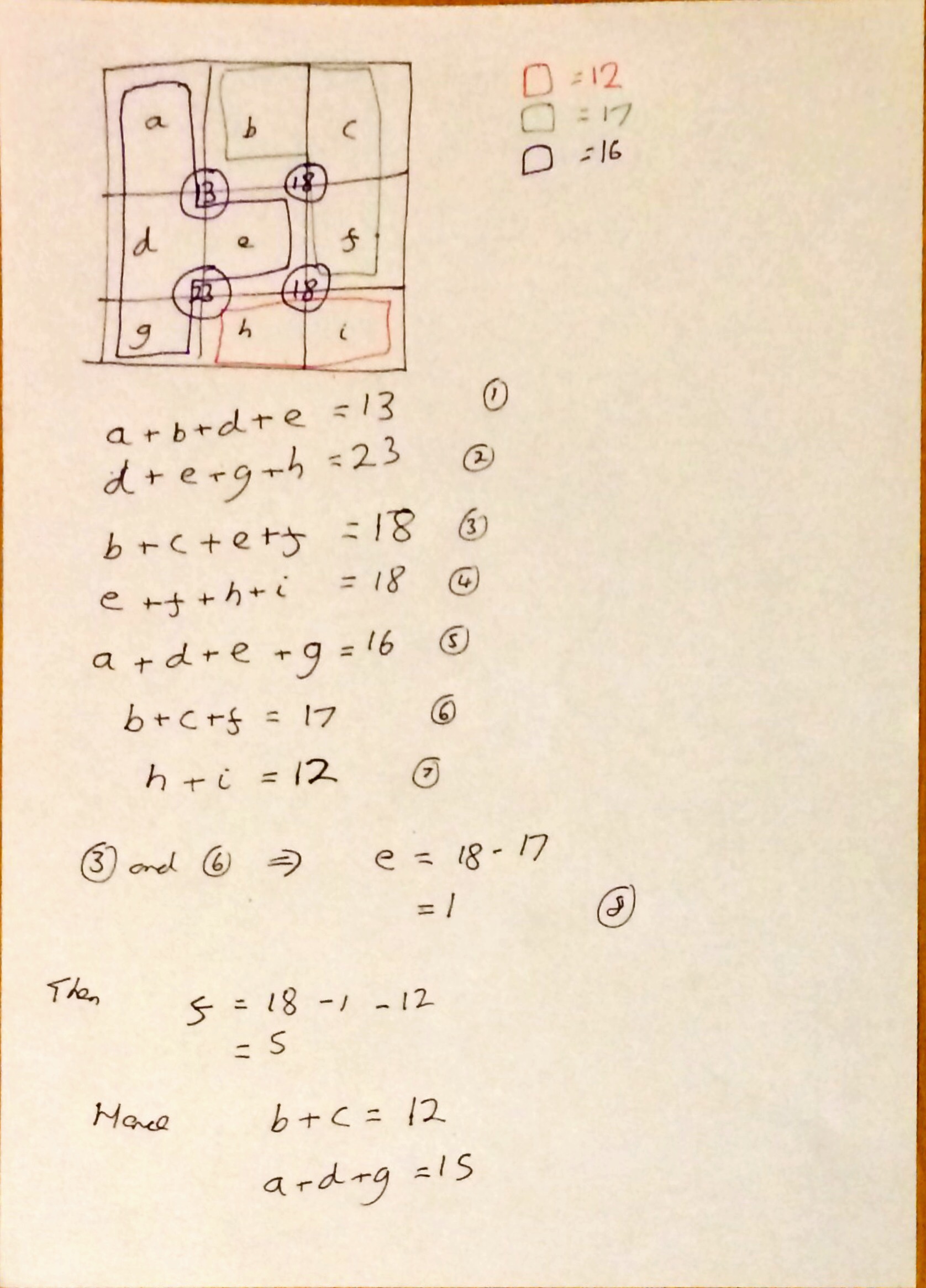

 To start with we have 9 unknowns and 7 equations so clearly an indeterminate system; hence brute mathematical force alone won’t be sufficient. Applying a bit of logic we can deduce two of the numbers. At this point I thought great, now I have 7 unknowns but 7 equations. However this was very foolish of me, as in fact we only really have 5 equations for our remaining 7 unknowns. And so, I had to make a few educated guesses on the likely magnitudes of some of the unknowns based on the totals that they contributed to. Once I had done this, the other unknowns dropped out fairly easily and a quick verification at the end showed that I had all the values correct. It could have been different though if I had been incorrect with these educated guesses.
To start with we have 9 unknowns and 7 equations so clearly an indeterminate system; hence brute mathematical force alone won’t be sufficient. Applying a bit of logic we can deduce two of the numbers. At this point I thought great, now I have 7 unknowns but 7 equations. However this was very foolish of me, as in fact we only really have 5 equations for our remaining 7 unknowns. And so, I had to make a few educated guesses on the likely magnitudes of some of the unknowns based on the totals that they contributed to. Once I had done this, the other unknowns dropped out fairly easily and a quick verification at the end showed that I had all the values correct. It could have been different though if I had been incorrect with these educated guesses.
So I have a few unanswered questions
- Have I missed something? Could I have done it without these educated guesses?
- Could I remove one condition and the solution still be unique?
- Would colour totals split into 3,3,3 squares instead of 2,3,4 lead to easier or harder puzzles?
I shall ponder these….
10 replies on “Suko”
I suppose I did something similar to you, but I left out any linear algebra techniques. After finding the 1 and 5 from the orange and red colors, I listed all possible combinations for each color. For red, there were two combinations left (A: 9,3 and B: 8,4); for orange, there were two possible combinations (A: 9,5,3 and B: 8,5,4), and finally for white there were 6 combinations.
Looking only at which combos work with each other, we get that only AB followed by white’s (1,2,6,7) and BA followed by white’s (1,2,6,7) work.
This means that white is 1,2,6,7. For ordering, we see that the top right corner must be the same as the sum of the top left and middle left. Looking at the numbers, the only choices are 2,6 or 2,7 for the white top left and middle left (to add to either 8 or 9). It’s unreasonable to expect the middle left to be 2 and still have the bottom left 4-square add to 23 (so with an educated guess), we have the two possibilities completely fixed now:
2 – 4 – 8
6 – 1 – 5
7 – ? – ?
or
2 – 3 – 9
7 – 1 – 5
6 – ? – ?
Worth noting that this “educated guess” can be wholly confirmed by imagining we did let the middle left be 2, then that means we would need the bottom left and bottom middle add to 20, which is absurd.
Finally, we look at the bottom sums and see that the second option does not work with 8 – 4 because we will only get a sum of 22 and not 23. So we are left with the correct solution of
2 – 4 – 8
6 – 1 – 5
7 – 9 – 3
Thanks for the puzzle
I always enjoy seeing how people have enjoyed playing my puzzles, and how they continue to tax the minds of players! I also enjoy seeing the different solving methods used by the wide variety of people playing Suko and Sujiko around the world. Thank you for this post.
Happy puzzling! 🙂
My solution is similar to Zero’s.
From the orange cells, we can determine that centre cell (e) is 1
The centre cell(=1) + red cells(=12) + f = 18, so f = 5
So b+c = 12, as does h+i. Only 9,3 and 8,4 are valid, (7,5 is impossible, as f=5)
Given d+e+g+h = 23 and e = 1, so d+g+h=22
h must be 8 or 9 (since if h was 4 or 3 then d + g = 22 – (3 or 4) = 19 or 18 – too high for 2 cells)
so d+g=14 or 13
As 9 and 8 are taken the best we can do is to make 13 with d and g set to 7 and 6 (and h = 9 ***)
Given h = 9 (and i=3), then b+c must be 8 and 4. In fact b must be 4 (if it were 8 then it would be too big as d is 6 or 7, e is 1 and a + b + d + e = 13). As b=4, then c=8. Only 2 is left so a = 2, and as b=4 and e = 1, d must=6 (to make 13) and finally g=7 completes the solution.
But my real reason for posting is to show another formula you can use which can be helpful for filling in all but the corner cells.
If we let A, B, C and D be the sums of the 4 grid squares (13,18,23 and 18 in this example), then you can prove that
b + d + f + h + 3*e = (A+B+C+D) – 45
Sometimes the above formula can be used to get to the solution even quicker.
For example, as before, e = 1 and f = 5.
Using the above formula b + d + f + h + 3*e = (A+B+C+D) – 45
we have b + d + 5 + h + 3*1 = (13 + 18 + 23 + 18) – 45
giving
b + d + h = 19
When we find that h = 9 (see *** above), we get b + d = 10. As e = 1, this means a = 2
It’s easier to use simple logic. Middle square must be 1 to make higher 18 total. Three of the white squares plus left-hand red square make 23, but same three white squares plus top left square make 16. Hence left-hand red square must be 7 greater than top left square. We’ve already used the 1 so it must be 2 and 9. Then the other red square must be 3, and we can put in 5 to complete the lower 18 group. The middle and right hand squares on the top row must total 12. Only possibility left is 4 and 8. 4 must be on the left or you get a duplicate 2 in the 13 group. Then 6 and 7 go in easily to complete the puzzle. It’s a lot quicker to do this than to write it!
Yes definitely quicker to do it than to write it!
May reply to this in another year’s time ! Meanwhile, does anyone know of any free software to solve Suko puzzles, including finding multiple solutions if any?
Hi Richard. There are sites such as [ http://www.herrmann.me.uk/script/puzzles.htm ] which offer help with solving Suko and Sujiko puzzles, along with Master Sujiko. I’ve not offered such a facility myself for two reasons – 1. Because others can build this kind of programming better than I can, and 2. I think it takes away from the challenge when the solution is only a click away! Still, as they say, different strokes for different folks! I must say that your working method on this puzzle is very much the same as mine [ I work through each puzzle manually when creating them, to ensure that they can be played by humans, as well as machines 🙂 ]. I’m chuffed to see people still playing, and enjoying my puzzles, so thank you for that.
Thanks Jai, my main concern was to find a way of checking for duplicate solutions. I enjoy doing the Suko puzzles in the Times newspaper.
you can solve this quickly using the diagonals rule: a+j must equal 5 because 45-(23+18-1) =5 so a+j must 2,3 and j must be 3 and h is then 9 (12-3). the other diagonal is 45-(13+18-)=15 which must be 8,7 (the 9 is already found) then the rest follows quickly… about 1 minute!
I have played around with the effect of swapping pairs of numbers over in the Suko puzzle. I am trying to establish what constraints there are around the values of the four internal totals (e.g 13 18 23 18 in the puzzle above). I can get combinations such as (21,21,19,19) and (19,18,17,16) and (17,17,17,19), but am coming to the conclusion that it will not be possible to have an arrangement of digits which gives all four internal totals the same. Does anyone have either an example that it can be done or a proof that it cannot?