On the 2nd November 1815 George Boole was born and in celebration he has been honoured by a Google Doodle.
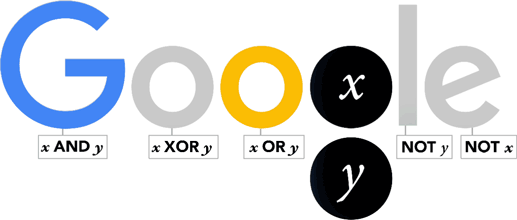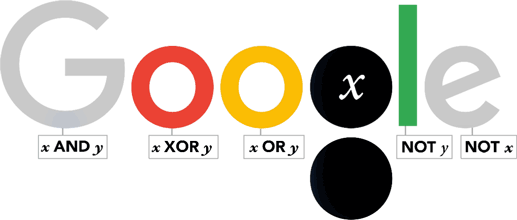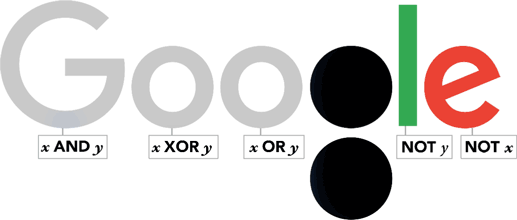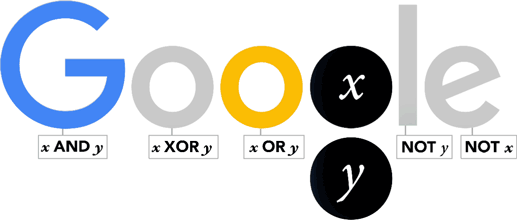
In addition the University of Lincoln’s mathematics and physics department organised a public lecture. to be given by Evegeny Khukhro
George Boole is credited with many things, including
- Founding invariant theory.
- Invention of boolean algebra.
- Intorduction of mathematical probability.
Boole’s first mathematical interest was is the realm of mathematical analysis and differential equations. He published two textbooks that also included soem original research contributions concerning thr algebraic approach to differential equations. Broadly speaking we denote the derivative as the application of an operator \(D\). So that if \(D(f) = u \) then \(f = D^{-1}(u) = \int u \). For example we could have the following Differential equation (DE) \( \frac{\mathrm{d}^2f}{\mathrm{d}x^2} + 3\frac{\mathrm{d}f}{\mathrm{d}x} + 2f = \sin (x) \) can be written in operator notation as \( D^2(f) + 3D(f)+2f = \sin (x) \) or \( (D^2+3D+2)(f) = \sin (x) \). For his contributions in this field he was awarded The Royal Medal of the Royal Society.
In 1841 Boole published one of the very first papers on invariant theory, this paper is credited by Arthur Cayley in his paper of 1845 which is often credited as being the start of invariant theory.
Of course Boole is most famous for his contributions in the world of logic. He first pulished a book on logic in 1847 whilst he was still in Lincoln, before publishing again once he had moved to Cork.
I was interested to learn that Boole only allowed the operation of Union when the sets were disjoint, Evegeny then presented a nice table comparing modern notation with that of Boole.
 Boole is also famous for his contributions to mathematical probability, most notably his name lives on in Boole’s inequality.
Boole is also famous for his contributions to mathematical probability, most notably his name lives on in Boole’s inequality.
In conclusion “Boole made a giant step towards mathematics as a truly abstract discipline, causing a paradigm shift, giving mathematics enormous scope and potency” (Khukhro, 2015). Evegeny has made his PowerPoint slides available here.
