University of Huddersfield Mathematics Teacher Conference

On Saturday 7th November Ed Southall (@solvemymaths) organised a morning’s conference. This was primarily aimed at his trainees but a few tickets were made available generally. It was definitely worth making the trip up the motorway in the awful rain to go to this and was great to catch up with Ed, Hannah  (@MissRadders) and Beth (@MissBLilley) afterwards. Andrew (@ApApaget) and Megan (@MeganGuinan1) but I didn’t realise until the end.

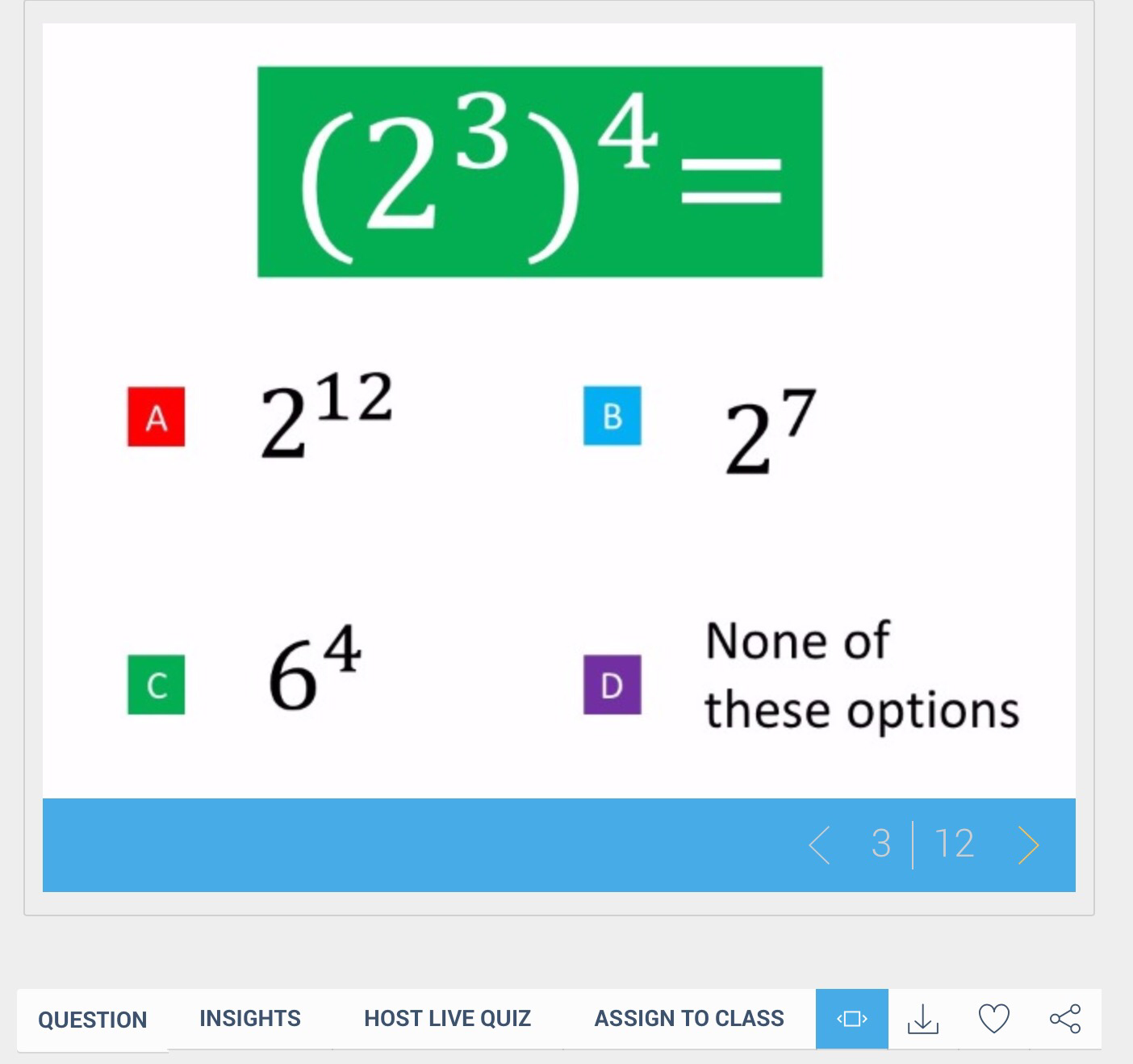
The day started with Craig Barton (@mrbartonmaths) talking about his excellent Diagnostic Questions website. I confess that as yet I hsven’t really used this website to its full potential but it is one that I want to explore more. The GCSE Maths Essential Skills quizes are excellent (a question from one of these is shown below) as each of the multi-choice answers exposes a misconception on a common GCSE topic.

 

Craig’s weekly insight blogs are excellent and well worth a read, I found the one about writing algebraic expressionsparticularly interesting.

Another feature of this website that I like is that students have to explain their reasoning (admittedly a contentious issue at the moment) when they select an answer which is great information for the teacher to have. If they make a wrong selection they are shown a range of correct explanations from their peers.

After Craig I went to the lovely Beth’s session on using the history of maths to help teach maths.

  I learnt a few fascinating things about the Greeks that I didn’t know, including an ingenious method to measure the radius of the moon.

 

Beth has written a great (first) blog post about her presentation here and has allowed her files to be made available either on TES or here.

Following Beth’s presentation I went to Laura Hadfield’s workshop “Making Differentiation Visible Throughout the Lesson”. For me there wasn’t much new here, but I was really interested in how everything in her lessons is traffic-lighted for differentiation. She doesn’t use the usual traffic light colours instead going for blue for “Practise”, green for “Mastery” and pink for “Apply”. I do something along these lines in some lessons, but certainly not in every lesson and it was interesting to hear of a department where this is a consistent practise. Like most things, I imagine it has more of an impact when consistently done. One comment that Laura made intrigued me – she said something like “there is no problem with using textbooks as long as the instructions aren’t ‘do question 1 to question 20’.” To me this is a problem with the textbook, not the instruction. If the textbook is well designed then working through a sequence of questions should develop fluency and understanding well. Admittedly there would have to be some teacher intervention but a good textbook would have pedagogically well designed questions.

To end the day we had the legend that is Don Steward present some excellent things. This was genuinely the best hour and a half of CPD that I have had.

Don opened with the following picture (I think the inquiry maths prompt has been inspired by this) as an investigation to do with Year 7 – “Do we get the same a nswer if we go either way round the diagram?”. Following a discussion students can then substitute some small numbers in and  investigate what happens: Is there a pattern? Can this be generalised? What if we change the numbers/operations  on the branches? I really liked his suggestion of how to introduce algebra into this task and it is definitely something I am going to try in the classroom. The idea being that when asked “how do we show this for all numbers?” many students will suggest trying a big number such as a million, but we can’t fit all those zeros into the circle and so we write ‘m’ and work through creating an algebraic expression. I think this is a fantastic way to introduce algebra in a non-threatening way. He then moved on to suggest that a student should think of a number  (Beth must have been very excited to be included in Don’s presentation here!) but not say what it is, so we have to give it a letter, ‘b’ say. We then pass this through the operations deriving the same expressions, but as we don’t know what this letter stands for we have shown that the pattern always holds. Don has also written this activity up back in 2013 in his excellent post “Both Ways”.There was a large emphasis in Don’s session on visual representations for proofs, and Ed has posted the visual proof of this pattern in his write up of the session.

Don then talked about some great proofs that made use of the following diagram

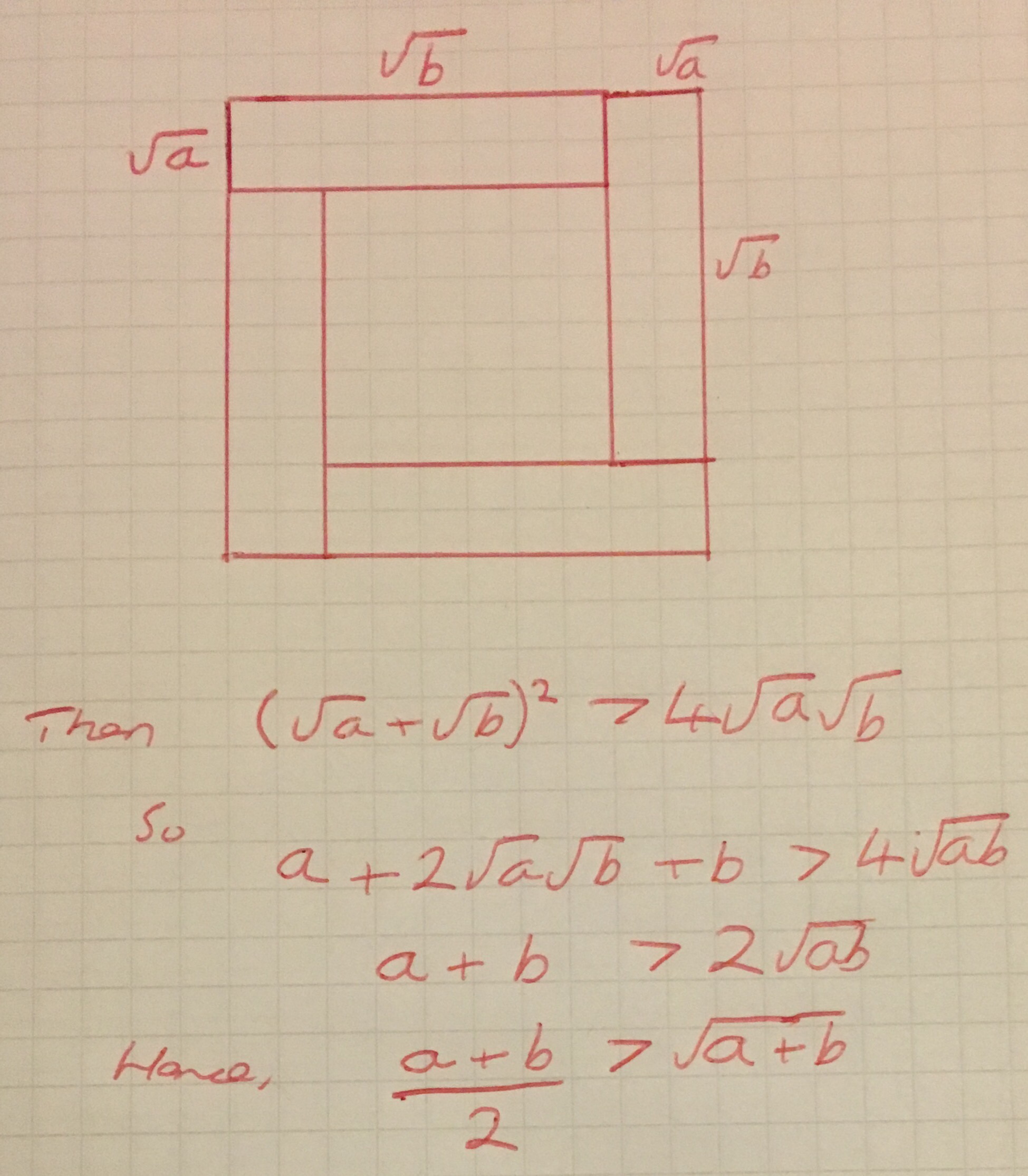
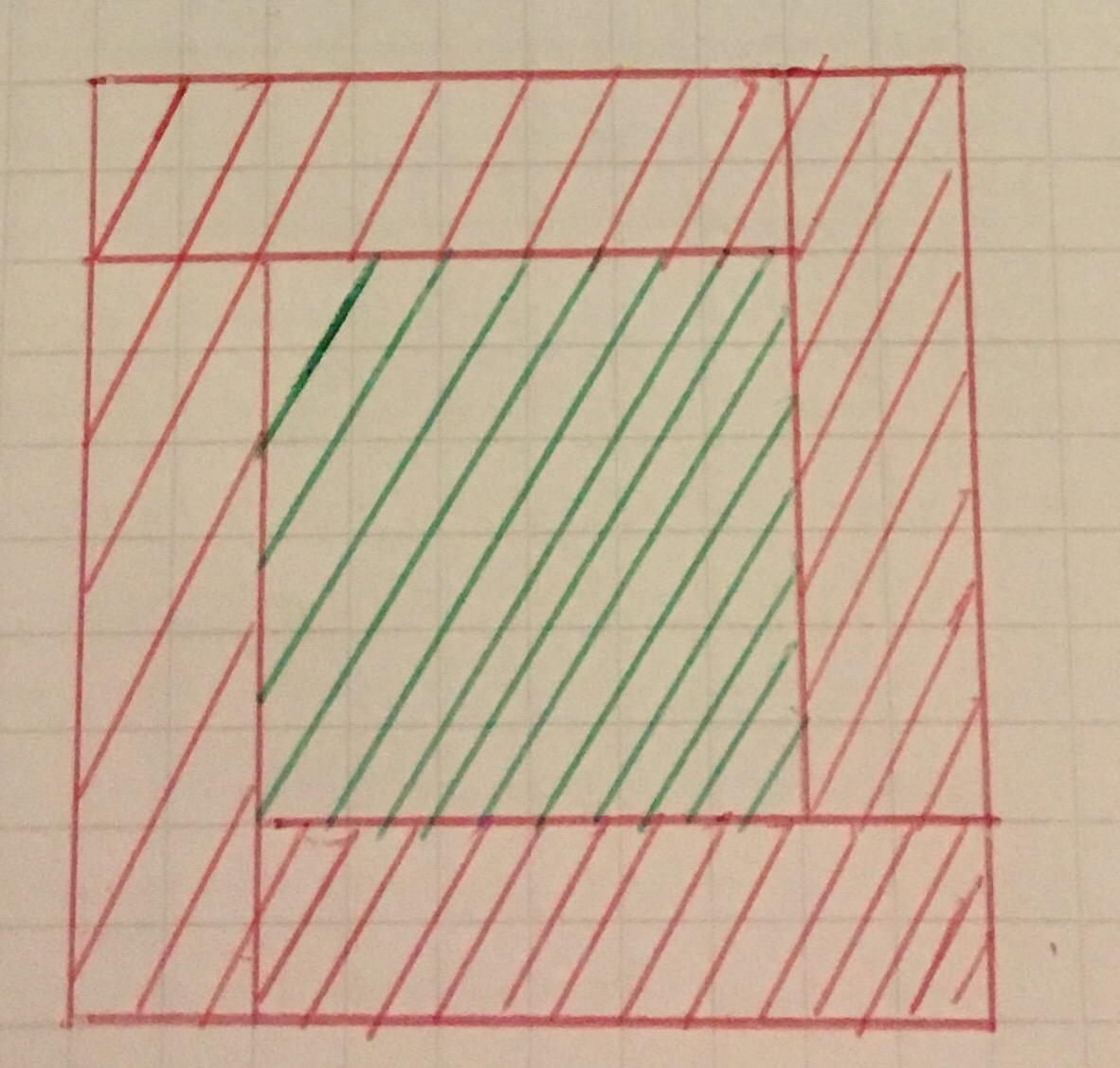 I particularly liked the one for the arithmetic-geometric mean inequality (or two numbers) shown below:

 Don then discussed some investigations involving relationships between the area and perimeter of rectangles – he has recently written about these on his blog here.

I was also pretty excited to see an alternative construction of an angle bisector that is is considerably easier than the one traditionally taught.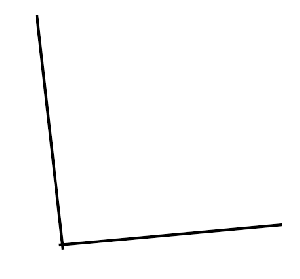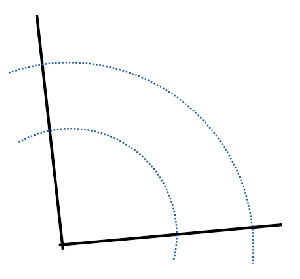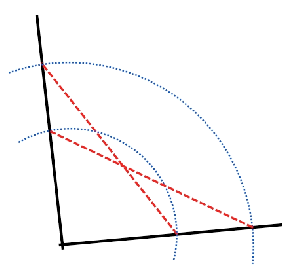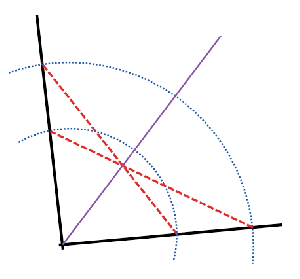 

The session ended on a mathematical approach to Magic squares, but Ed has written an excellent post about this, so head over to solvemymaths.com for more details.

Overall I had a fantastic morning in Huddersfield, thank you Ed for organising this.