I may be wrong, but it seems un-common to introduce the Poisson distribution in S2 by discussing its original application to real data. Before teaching in schools I developed an “Introduction to Quantitative Research Methods for Engineers” course and this was how I introduced the poisson distribution in the lecture notes. I think it is a great way to bring a bit of the history of mathematics into your teaching, and in my opinion certainly motivates the Poisson distribution more than the fairly awful way it is introduced in the Edexcel text book.
The distribution function for the Poisson distribution is as follows: If \( X \sim Po(\lambda) \) then \( P(X=x) = \frac{e^{-\lambda}\lambda^x}{x!} \)
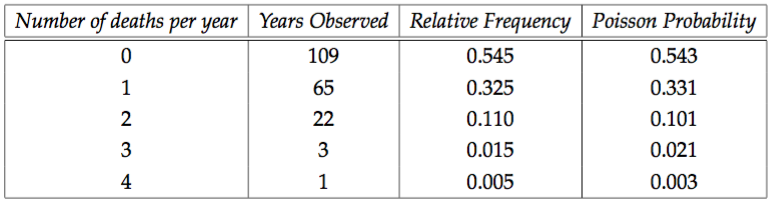
In L. Bortkiewicz’s book of 1898, “The Law of Small Numbers” he discusses the number of fatalities in 10 corps of the Prussian cavalry that were the result of horse kicks. He has 200 years worth of data, and to this data he fits a Poisson distribution after calculating an appropriate rate parameter.
From the table it is clear that a Poisson distribution, with rate parameter \(0.61\) provides a pretty good fit (of curse the goodness of fit can be calculated!).
As an aside, tabulating Poisson probabilities is extremely tedious… You can save yourself a lot of time by using WolframAlpha, especially if you know some Mathematica / Wolfram Language syntax.For example to tabulate the values for a Poisson distribution woth rate parameter 2, for example you can do the following
In the above the command “N[Table[(Exp[-2]*2^x)/Factorial[x],{x,0,10}],4]” generates the following
Here I have used the Table command to tabulate between \(x=0\) and \(x=10\) the Poisson distribution function with parameter \(-2\). I have then wrapped this with the N command so that I get values to 4 decimal places output instead of the default exact expressions.
Whilst WolframAlpha’s natural language processing is good, using the syntax of the underlying language makes it a lot more powerful.


2 replies on “Introducing the Poisson Distribution”
Nice call back to the Grad School. I’ve lost count how many times I’ve gone through this example with graduates! It’s a nice introduction to the Poisson distribution.
Cheers Tom. Yes I don’t get why more people don’t use this example…