This morning I made the journey down to the University of Leicester’s Fraser Noble Building for the latest ATM/MA East Midlands branch session.
Today it was John Mason – a big name in the Mathematics Education world. His session was entitled “Teaching More by Teaching Less: Getting Learners to Make Use of their Natural Powers” and I had a great time at this thought provoking session and I was lucky to sit with Pete (@MrMattock), Mel (@Just_Maths), Em (@EJMaths), Andrew (@ApApaget), Mary (@PardoeMary) and Andrew Price (@ColonelPrice) where we had many great conversations. It was also good to see a strong contingent from The University of Nottingham’s CRME in attendance.
For this post I am going to share some of the tasks we looked at and my thoughts on them, but I’m going to start with a few nice quotes from John Mason himself.
- “Mathematics is working on problems.”
- “Learning to read graphs is much more important than learning to draw graphs.”
- “My job is not to choose questions kids find attractive, it’s to choose questions with the most potential for learning maths.”
Sadly I think these three highlighted thingd probably happen far too little in the classroom today with all of the current assessment and accountability pressures.
One thing from the sesssion that I liked straight away was the use of magic squares without numbers.I love using magic squares in lessons, but I admit I tend to use them as a way of practising procedues, I hadn’t thought of using them to “tease out” students’ reasoning. John pointed out that there was lots of research that students who have been deemed “low achievers” in mathematics can reason mathematically, it is their low level of numeracy that gets in the way of them demonstratng this in the classroom – so why not use tasks that don’t require numeracy. I firmly believe that improving numerarcy is important, but so is developing the mathematical reasoning skills and so I like the idea of using tasks that develop this without requiring a high level of nmeracy. Indeed, I suspect that developing reasoning will improve their numeracy anyway as the students will be able to reason more about the number system. Fo those of you who aren’t familiar with magic squares, they are arrays of numbers (commonly \(3 \times 3\) such that the column sums, row sums and leading diagonal sums are all the same. John suggested removing all the numbers from a magic square and using just mathematical reasoning to show certain properties. He started by asking us to reason out that the blue coloured squares in the magic square below add up to the same value as the red coloured squares.
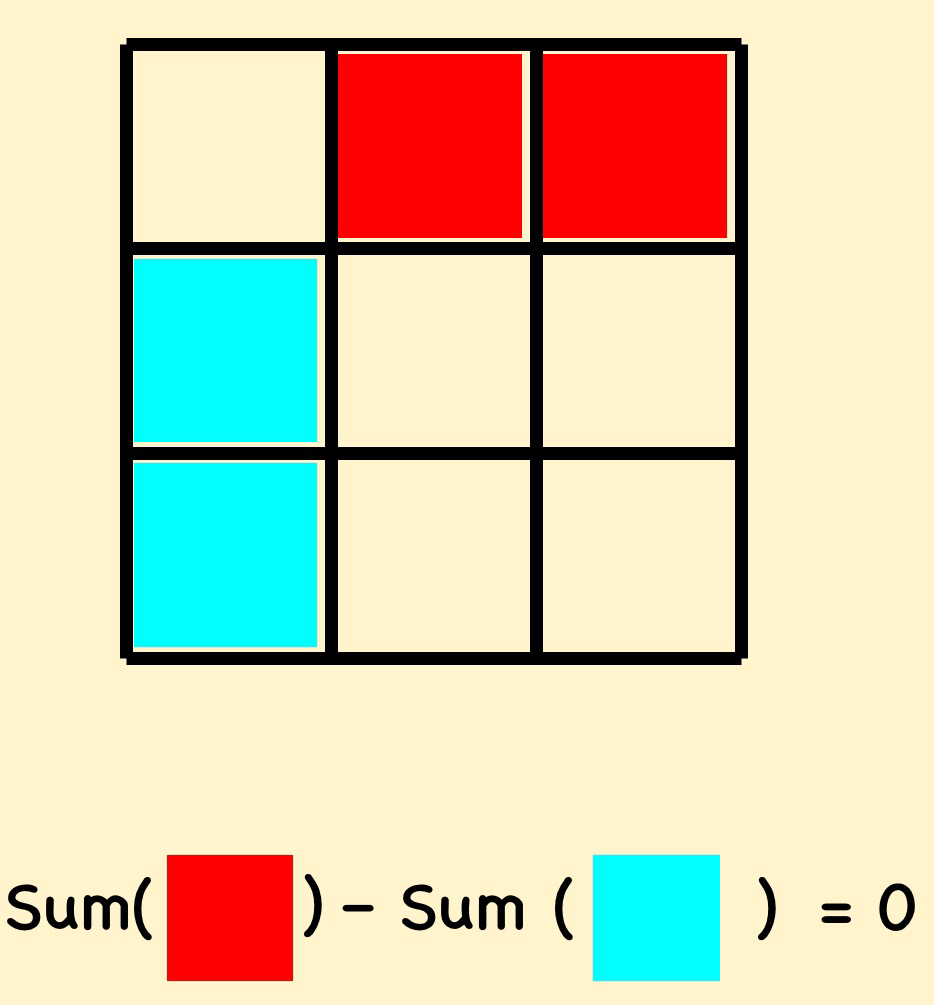 Of course this is relatively clear, but you can develop this idea into some harder examples
Of course this is relatively clear, but you can develop this idea into some harder examples
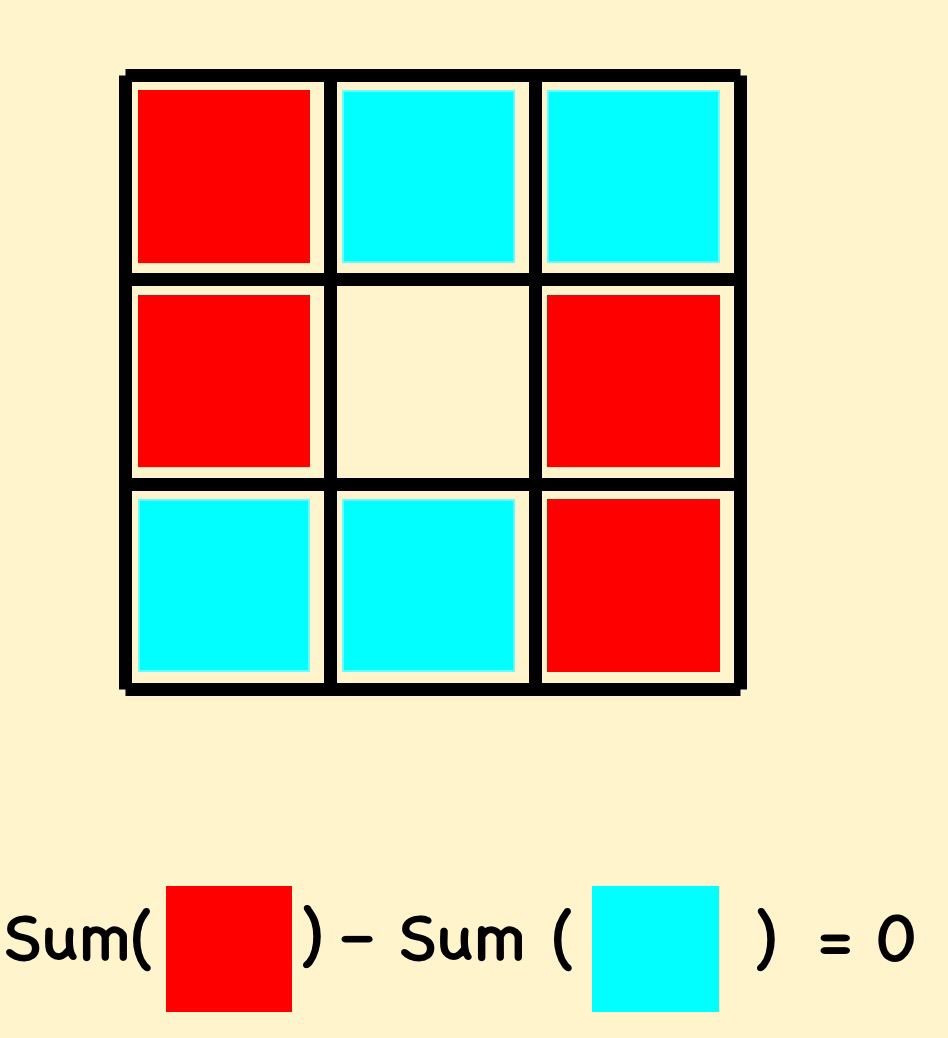 Or even extend the idea to larger magic squares
Or even extend the idea to larger magic squares
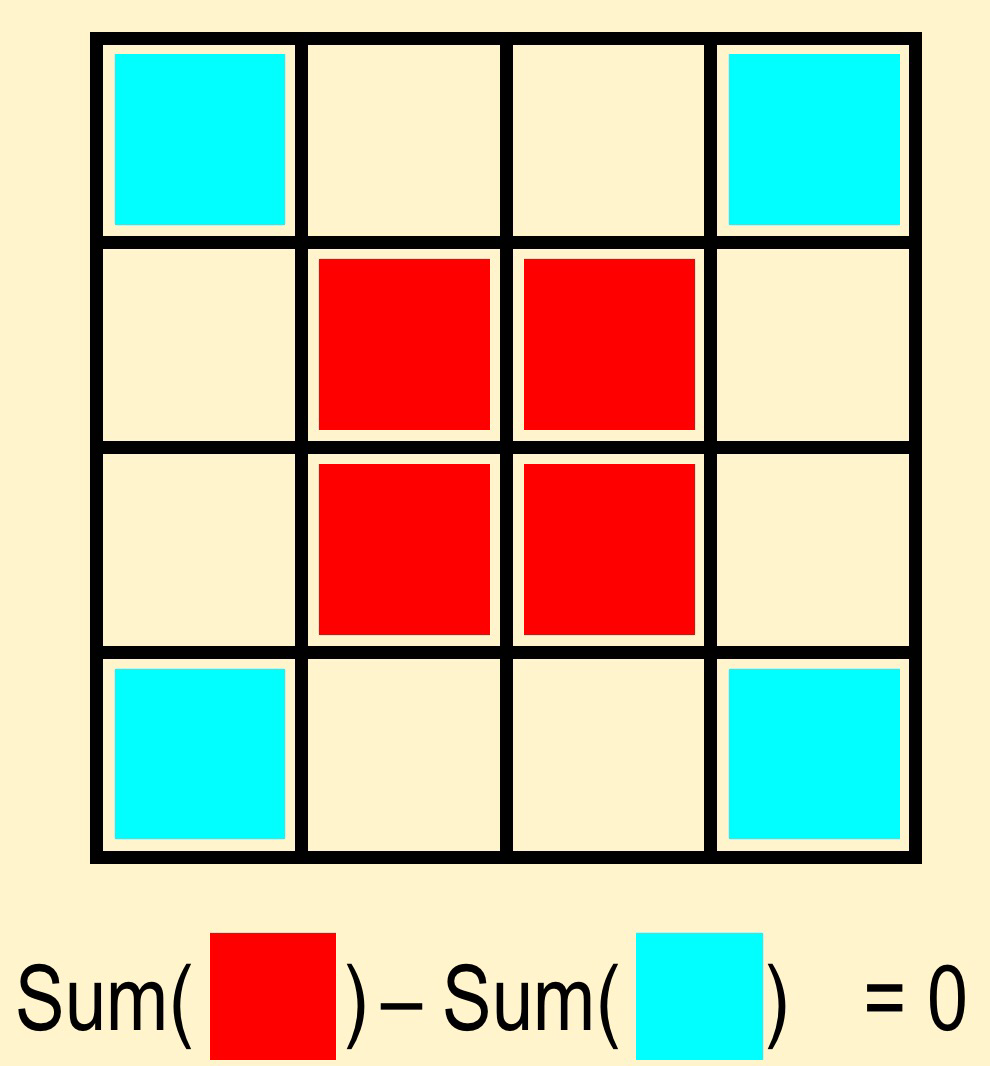
I am definitely going to try this in the classroom.
This session has also inspired me to use more prompt photos and as students to formulate their own mathematical questions. Of course it is important for students to develop fluency, but I also think that to become a mathematician they need to be able to pose interesting mathematical questions.
John showed a vey cool applet that he has written using Cinderella. It contained a straight line of fixed length divided into sa blue section and a red section. The blue line segment was the perimeter of a square and the red line segment was the perimeter of a triangle and as the joining point moved from left to right the square gre and the triangle shrunk as you would expect. One interesting question to pose is “At what point is the perimeter of the square equal to that of the triangle”. Of course this is true when the join of the red and blue line segments is in the middle, but originally I (along with many others) made the mistake of thinking that we had to work with he ratio of the side lengths. The app allows you to plot the area and perimeter of the two shapes as the joining point moves, as shown in the video below.
This is a fantastic visualisation of something that I actually found quite counter-intuitive until you think about it in terms of the underlying maths. There are many other questions that you could pose about this visualisation.
We then looked at some more tasks around the topic of area and perimeter from this excellent sheet that John provided us with
 I particularly like the “More or Less Perimeter and Area” and “Shape Signature” tasks and would quite like to work them into lessosn this year at some point. I really want to find the time to explore the questions posed by the “Shape Signature” task.
I particularly like the “More or Less Perimeter and Area” and “Shape Signature” tasks and would quite like to work them into lessosn this year at some point. I really want to find the time to explore the questions posed by the “Shape Signature” task.
Towards the end of the session John talked about “Multi-Level Initiating of Tasks”:
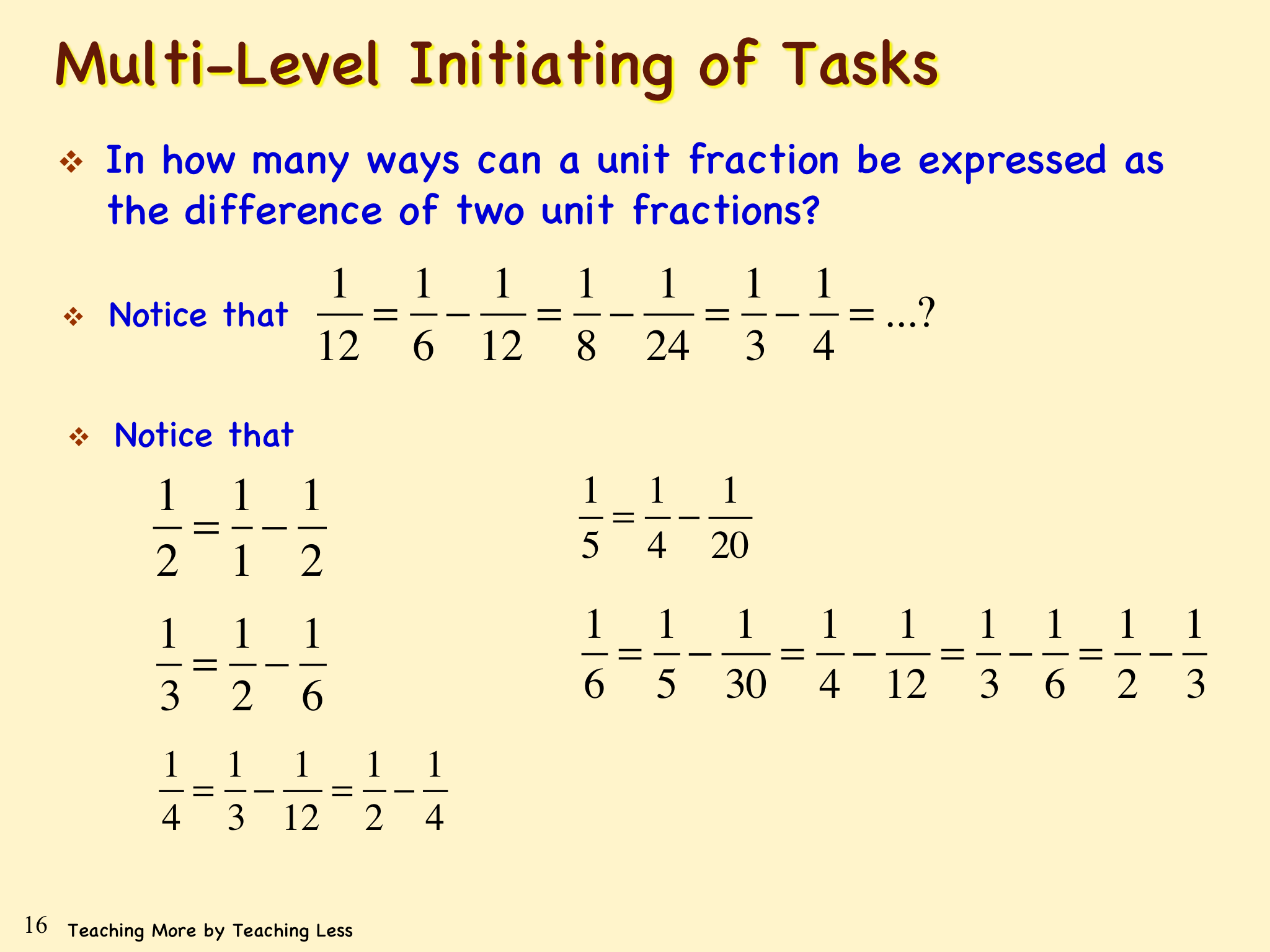 Between the three there is clearly an increase in the structure and scaffolding given to the student. At what point does this turn from beig a help to leading to a dependence on the part of the student and reduce their ability to reason mathematically?
Between the three there is clearly an increase in the structure and scaffolding given to the student. At what point does this turn from beig a help to leading to a dependence on the part of the student and reduce their ability to reason mathematically?
All in all it was a very thought provoking session and I have taken away lots of things to ponder. John has kindly made all the materials from his talk available online here; in particular his PowerPoint slides are available.
2 replies on “John Mason – Another ATM Session”
Thank you for this write-up of your experiences of JM’s session. I felt privileged to be there and to have the pedagogic part of my brain rattled on so many occasions. Regards Mike
I do miss ATM! Have been retired eighteen years now, but I heard and was inspired by John Mason at an Easter Conference.
(and yay for Leicester! My late parents hailed from there . . .)