In December last year I had a review of the MEI/Sigma Network’s game published in the IMA magazine Mathematics Today. I later published an expanded review on my blog in December. Check it out if you haven’t already.
Richard started by talking about himself and saying that his first experience with computers was when he was bought a ZX81 for Christmas in 1982. As an aside my first experience with computers was on a BBC Micro at primary school. Richard explained how programming increased his enjoyment of mathematics – an experience that certainly resonates with me.
Richard completed a PhD at Warwick and after lecturing for a while became involved with the Further Maths Support Programme, before in 2014 taking a job at MEI developing online resources for teaching and learning maths.
There are many great reasons why games are good medium for learning mathematics, Richard highlighted that when gaming you expect to make mistakes and it creates a non-threatening environment for students to try things out. He also highlighted the reasons shown below:
 What does a good maths game look like?! Richard’s criteria are these
What does a good maths game look like?! Richard’s criteria are these
- Encourage students to practise lots of examples
- Provide a representation of mathematical problems in a more accessible way.
- Have a mechanic which has a “physical” connection to the mathematical idea.
- Give players lots of choice about what they can do at any given moment.
If you look on the App Store the vast majority of maths games fall into the first category, promoting practise of key skills such as multiplication facts, basic numeracy etc.
I hadn’t seen Keith Devlin’s game Wuzzit Trouble before (even though I had heard about it) – I feel that I need to investigate this some more now. Richard also completed a secondment developing some games as a consultant to Manga High and he discussed some of the games he helped develop while there including Ice Ice Maybe and Algebra Meltdown – again Manga High is something I really should explore more..
It was fascinating to hear about the development of Sumaze and how it developed out of this initial idea which Richard felt didn’t have enough variety as a game:
 Following this he began to consider the idea of moving through squares to get to a target value as a way of teaching something, specifically he looked at developing some of the ideas that led to the logarithm levels in the online version of Sumaze.
Following this he began to consider the idea of moving through squares to get to a target value as a way of teaching something, specifically he looked at developing some of the ideas that led to the logarithm levels in the online version of Sumaze.
The Sigma network then funded the production of a web-based version covering more mathematical topics and for an App version. To develop the app a maths startup company MathsCraft was engaged to provide the graphics, sound and menu version.
I hadn’t thought too much about the game mechanics before so it was nice to be told a bit more about that. Specifically only nested expressions with only one variable are permitted and so the game can’t test things such as \(x^3+6x\) or \(log(xy) = log(x)+log(y)\). Richard explained that the decision was made to not include things like memory blocks or multiple blocks which would have allowed this kind of thing as it would detract from the gameplay. I think this was probably the right decision – the inclusion of these would have made the game seem a lot harder to play, and probably not add too much in terms of mathematics.
Richard then talked about the mathematics underlying a couple of the levels:
Negatives 13 -Gridlock Here, if you think mathematically you need to find the fixed point of the function \(f(x) = -3(x+12)\) to get the correct value once you have passed through all the modifier blocks. I certainly hadn’t thought of it like this when I played this level.

Powers 10 – Binary Finery Here the level is asking you to find the binary representation of 61.
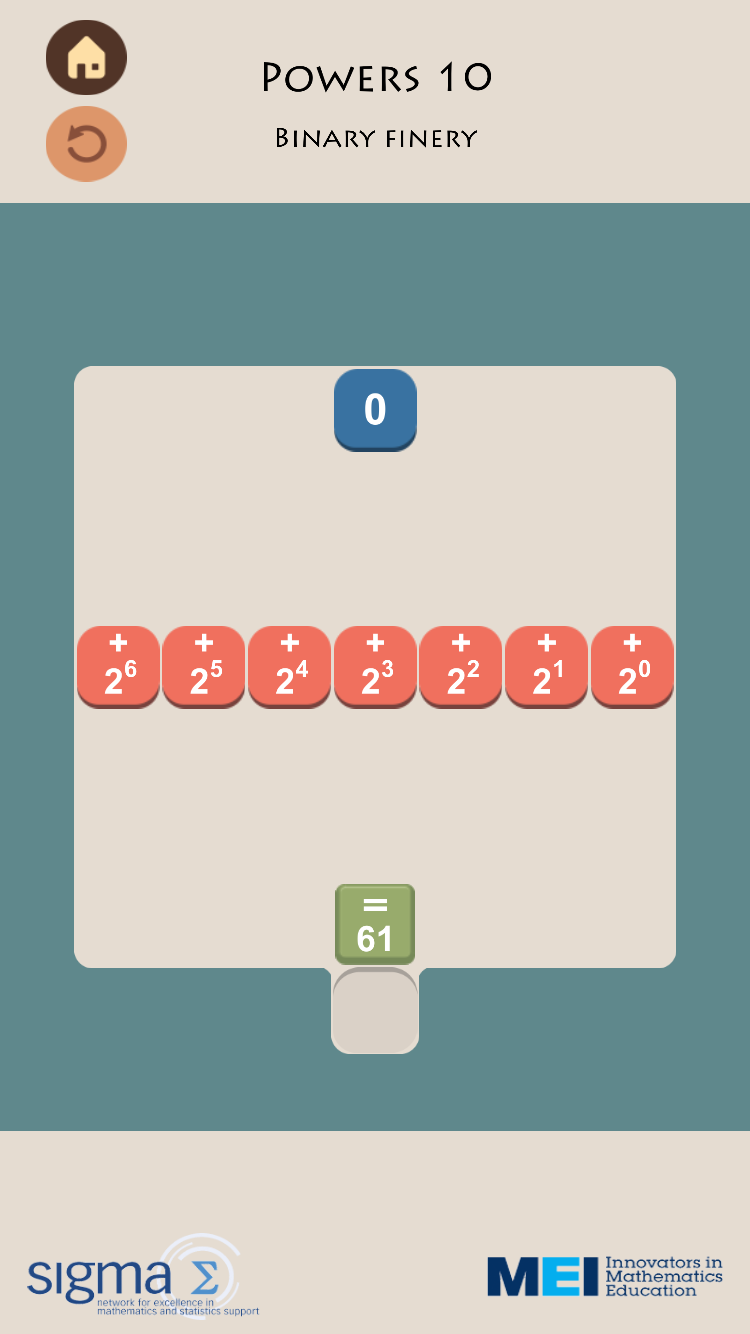
As of 8th February 2016 Sumaze has had over 17,000 downloads since the 20th October and another version dealing with lower level numeracy topics is planned.
There was a very good question about the game mechanic versus the conventional order of operations. For example the operations are applied consecutively and don’t follow the conventional rules, for example in Sumaze 3 + 2 multiplied by 3 would give 15 as opposed to 9. I, like Richard hadn’t considered this before as I had seen the blocks as functions that are applied to an input but I guess this could be an issue for students. What do you think?