Before I started teaching A-Level I hadn’t done an integral by hand for about 5 years – I would always use Mathematica when I had to evaluate an integral symbolically.
I’ve actually enjoyed re-familiarising myself with some of the techniques required for some of the more difficult integrands and fancied looking at some more challenging integrals and so I bought the book “Inside Interesting Integrals” by Paul J. Nahin. This is a great book packed full of clever tricks to evaluate integrals and I thought as it is the last day of the holidays (and so don’t want to write a long post) I would share one of them here.
It was nice to be reminded of the “flipping the integral’s variable’s direction” trick which works in a lot of places. For example consider the integral below.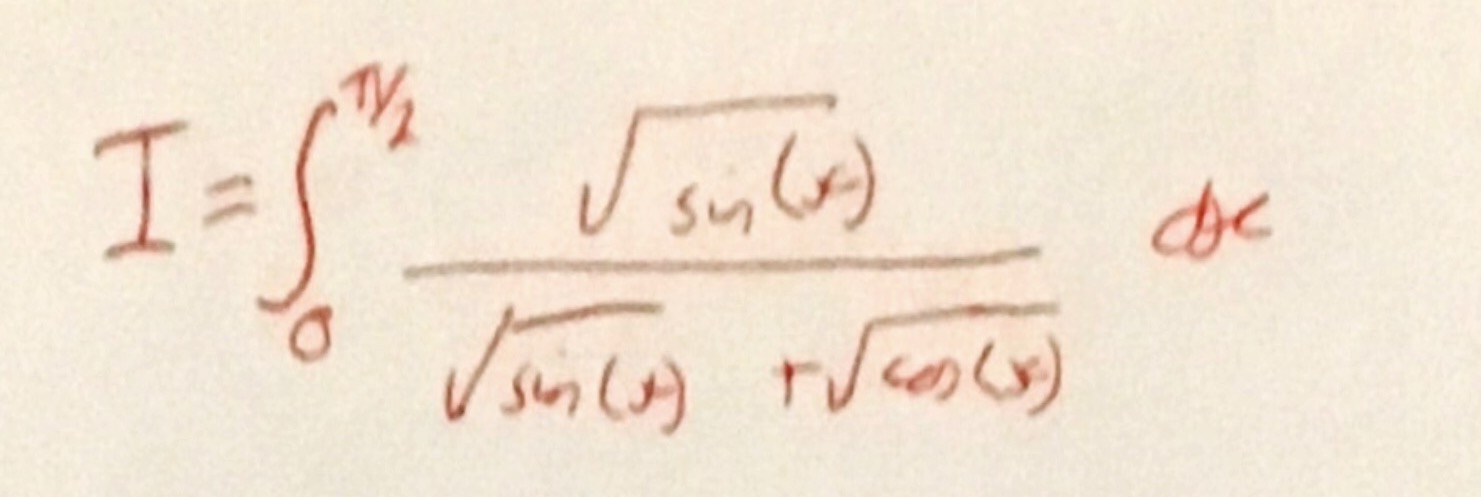
Make the substitution \(x = \frac{\pi}{2}-y \) and so \(dx = -dy\) which gives the following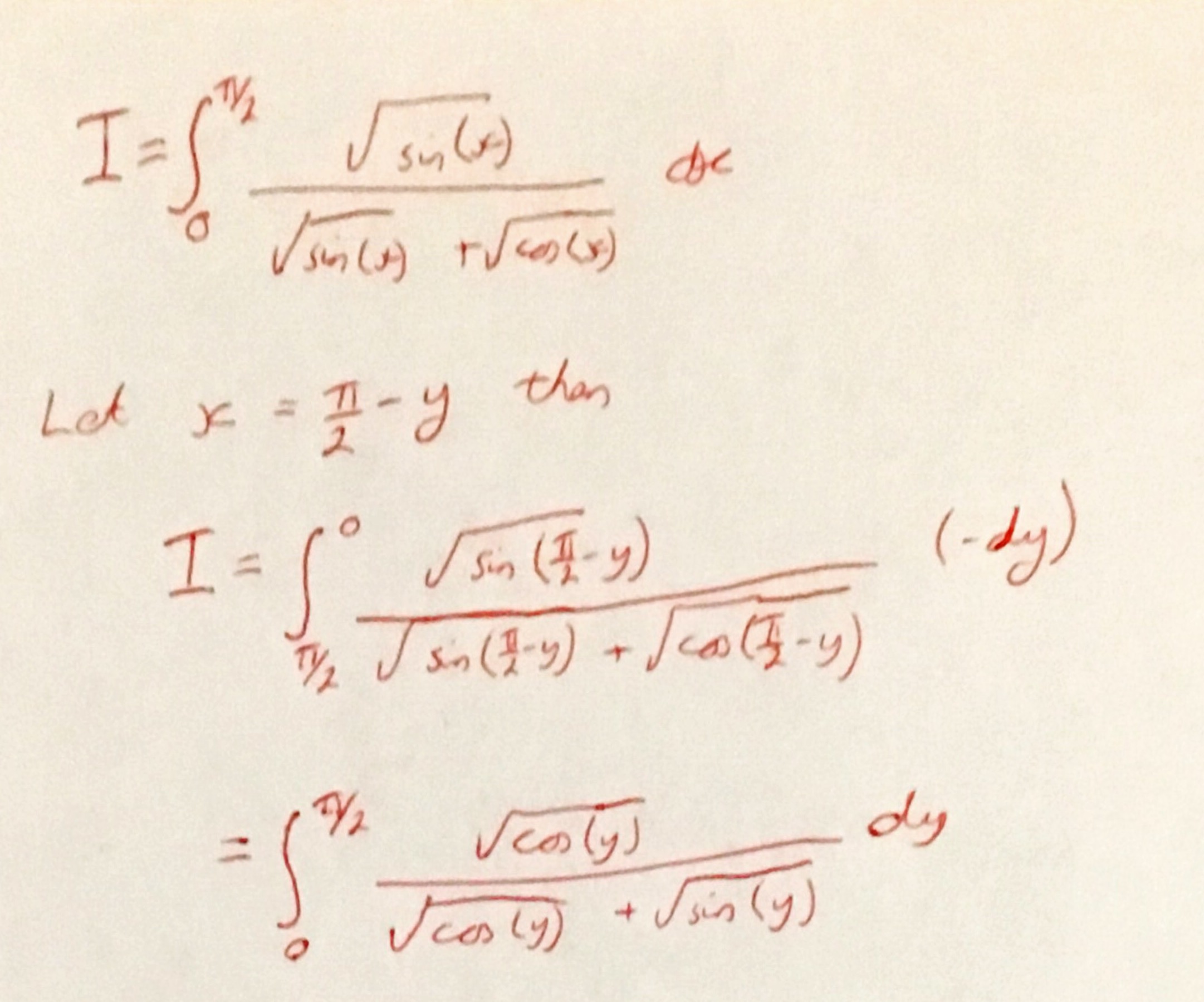
and so, by adding this expression to the original integral (and changing back the dummy variable of integration) you obtain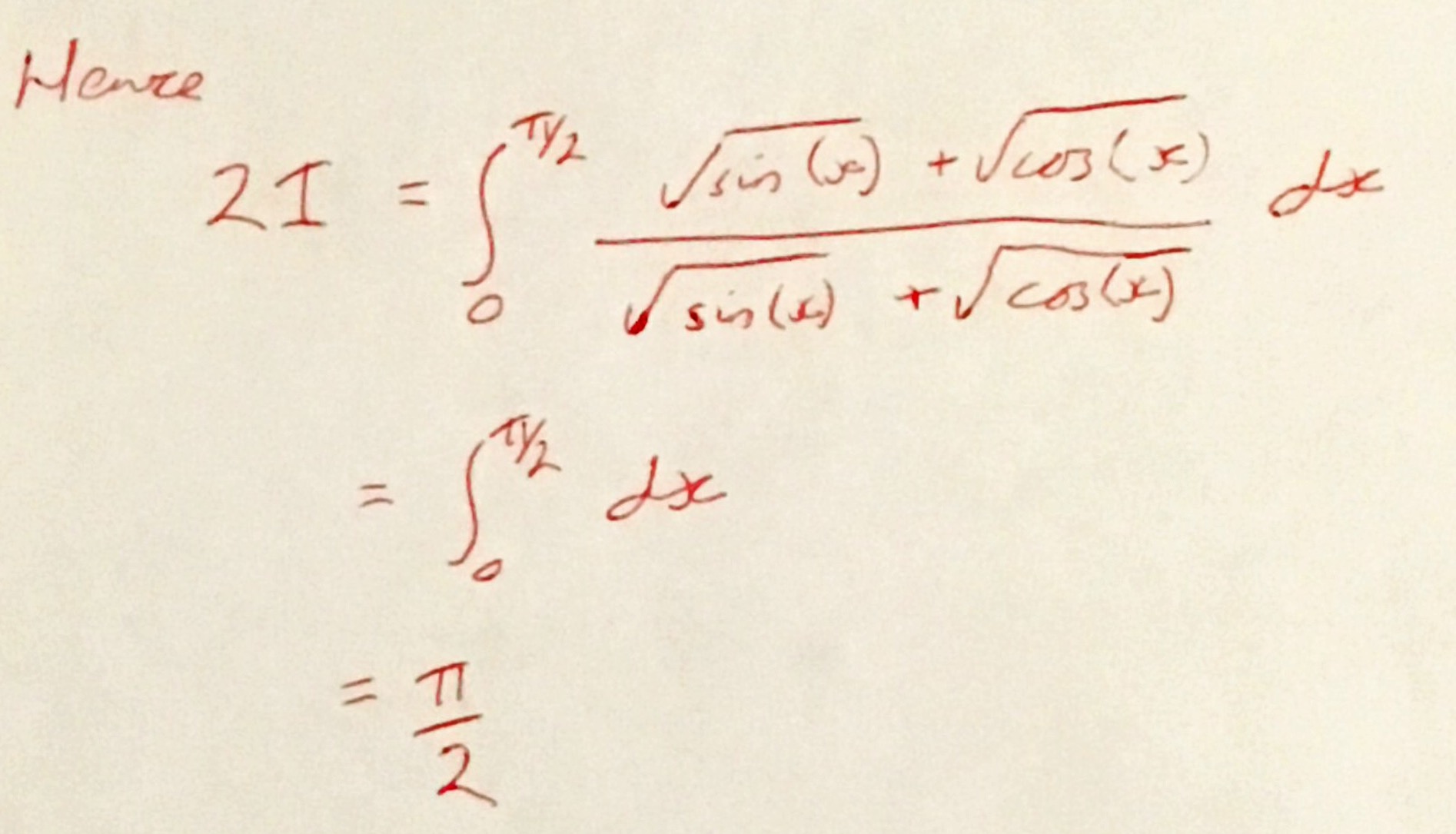
Hence, the original definite integral is equal to \(\pi / 4 \). I think this is pretty neat!
Here are some for you to try (you may need to pick a substitution as well as using the trick described above):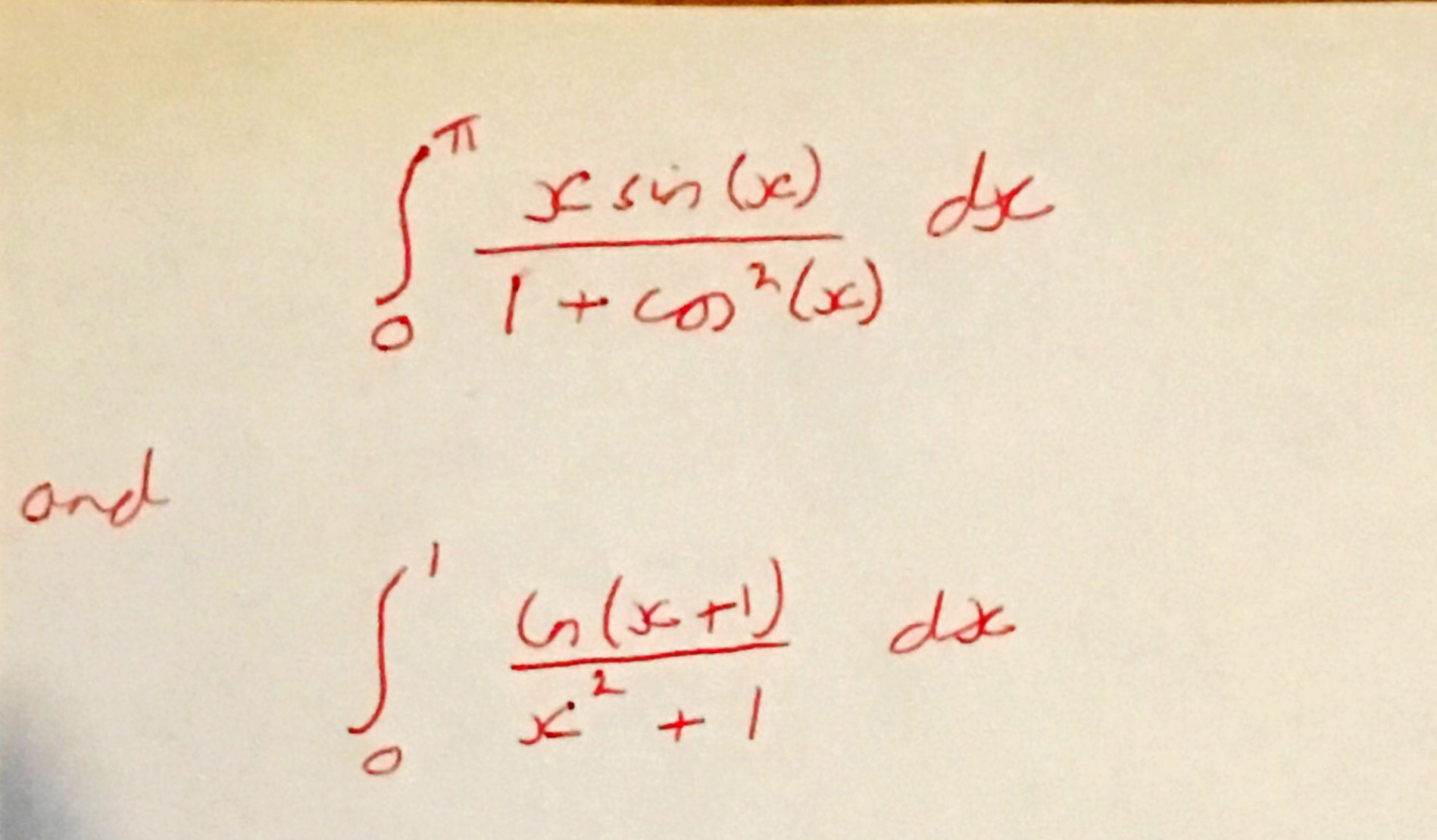
One reply on “An Integration Trick”
On the same theme, here’s a thing I did with a student a couple of years ago — enjoy! http://flyingcoloursmaths.co.uk/wp-content/uploads/2014/05/sneaky.pdf