On Tuesday 23rd of February I am hosting the NCETM’s #mathscpdchat on the topic of “Proving: how do pupils learn to do it?”. This post is a collection of some thoughts and opinions that I have had over the last week or so….
A month or so ago I watched this fantastic video from the Museum of Math in New York on the subject of “Proofs from the BOOK”, if you have an hour or so to spare it is well worth a watch:
To me the concept of proof is what sets mathematics apart from all the other sciences and gives me more faith in anything proved mathematically than a theory from another branch of science. As such I think it is crucial for students to be exposed to proof as early as possible (even if it is just by giving them exposure to the question “How can you be sure this will always work?”). To reduce mathematics to various procedures for performing calculations of one sort or another is a depressing idea.
Typically geometric proofs are see as a nice way to introduce proof, for example this proof of the expansion for \((a+b)^2 = a^2+2ab+b^2\) 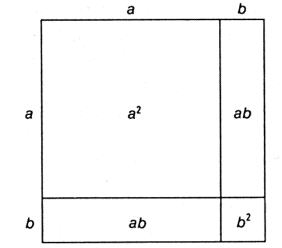
Personally I question whether geometric proofs are the best way to introduce proof to students as sometimes they struggle to see what the diagram is showing, don’t necessarily appreciate that some diagrams are only sketches etc.
I thought it would be interesting to see what some of my old colleagues (3 still in academia, one in teaching and one in industry) thought about teaching proof at secondary level – this is what they had to say.
Person 1:
“Yeah. I’m definitely for the idea but it’s about mathematical rigour and I’m not sure a lot of students would appreciate it at that age. At an advanced level, proofs are associated with theorems and methods. I think there’s very few topics you could apply it to, which make it accessible. Pythagoras’ theorem is one that comes to mind or other geometry related topics (angles, shape and area) are probably the most obvious and intuitive topics – but how do you make it interesting. I think it’s one of many advanced concepts that becomes harder to integrate into the early curriculum. Maybe with operations on fractions too?”
Person 2:
“I think it is a good idea to teach proof at secondary school level (although maybe KS3 is too early). The problem is at Uni level and higher proofs are important – if students haven’t learnt and understood them from an earlier age they do struggle. However, students who don’t go onto Maths (or other subjects where proofs are useful) probably won’t need/understand proofs – and you risk not engaging them. I’m not sure how to aim proofs at lower levels.”
Person 3:
“Good question, and in an ideal world, of course we should be teaching mathematical proof alongside everything else. Two problems: our “pure” idea of mathematics in terms of proof being the final word seems to conflict with others’ views of mathematics in terms of methods and formulae used to work out solutions to “real-world questions” – such as voltage in a circuit. So would people accept the idea that maths is actually all about proof, rather than bare calculations? The other is that proof does rely quite a bit on logic, and so you then have the question of how to introduce rigorous logic at KS2 or KS3. In particular, why proof by contradiction or counterexample works at all.”
Person 4:
“Regarding teaching proof to secondary school children, I think it’s important to introduce the idea to children at a much younger age than A Level. I’m not sure how much better the new A Level is, but it’s barely covered there, especially without Further Maths. I think this serves two purposes. It better prepares those students that go on to study maths at undergraduate level, which is the obvious benefit. The second advantage is that younger students will be exposed to another side of maths that is different and hopefully more interesting than just calculating things and doing sums. Other subjects, such as English, history, human geography start to get analytical from around Year 9 onwards and this typically engages students rather than putting them off, so why should maths be any different?
I think the way to do it is perhaps introduce the ideas first in the current way, such as Pythagoras’ Theorem, triangle inequality etc. and get them used to using the result so they are fairly convinced it works. Then motivate the question “how can we show that this works in ALL cases” to get them used to the idea of general ideas. Some may attempt to just do lots of examples, but will hopefully realise that no list is exhaustive enough and they need to try something else.”
Person 5:
“Proofs are fundamental throughout the whole of mathematics and they are what make mathematics so different to others sciences. Theories in other sciences are based on our best knowledge at a certain point in time, they can be backed up with evidence, but could be disproved in light of new experiences. Mathematical theorems, on the other hand, once proved, are fact. As an example, consider Newton’s laws of motion, for 200 years these were assumed to be fundamentally true, until Einstein (and others) showed that they did not hold at small scales and high speeds. In contrast, Pythagoras’ theorem is as valid today as it was 2,500 years ago in ancient Greece. For those wishing to study mathematics past A-Level, understanding how to prove things is essential; indeed, a large part of a professional mathematician’s work is taken up in the quest for new proofs. Exposure to as many proofs as possible will leave students with the building blocks to develop their own novel proofs. For those inquisitive students, who do not with to pursue mathematics further, attempting to prove a theorem can lead to better understanding of that theorem, as well as teaching the student the crucial skill of logical thought. Of course, for some students, proving theorems is not required, a firm grip on how to use the theorem is the most important thing, and this is OK too. By teaching students why we need proofs and how useful they can be, hopefully we can avoid situations similar to the one I faced when lecturing engineering students. I was told that ‘I did too many proofs’, when, in fact, I had done none. It has been a while since I was at school and I cannot recall exactly what exposure to proofs I had. I have this vague idea that I may have been proving things, but I didn’t know it. I am not convinced that developing proofs amongst KS3 students is required, except for those with a definite aptitude for the subject. For older students, I think it is vital they are told why proofs are so important in mathematics. If a theorem is given, and its proof is feasible, then I think it should be explored in class. Geometry and number theory seem to me the most accessible areas where theorems could be proved. Later, trigonometric theorems could be proved, as well as those fundamental to Calculus. Students should also be encouraged to come up with their own proofs, after all, there are often multiple ways to prove something.”
I think the quotes above throw up some very interesting ideas that could be discussed in our twitter chat, for example:
- Should all students of mathematics be exposed to proof?
- How should we develop the logical thinking required to prove something?
- Does not teaching proof disadvantage children?
- Do we need to reformulate the idea of “what maths is” for many people to understand the importance of proof?
- How do we make developing proofs engaging?
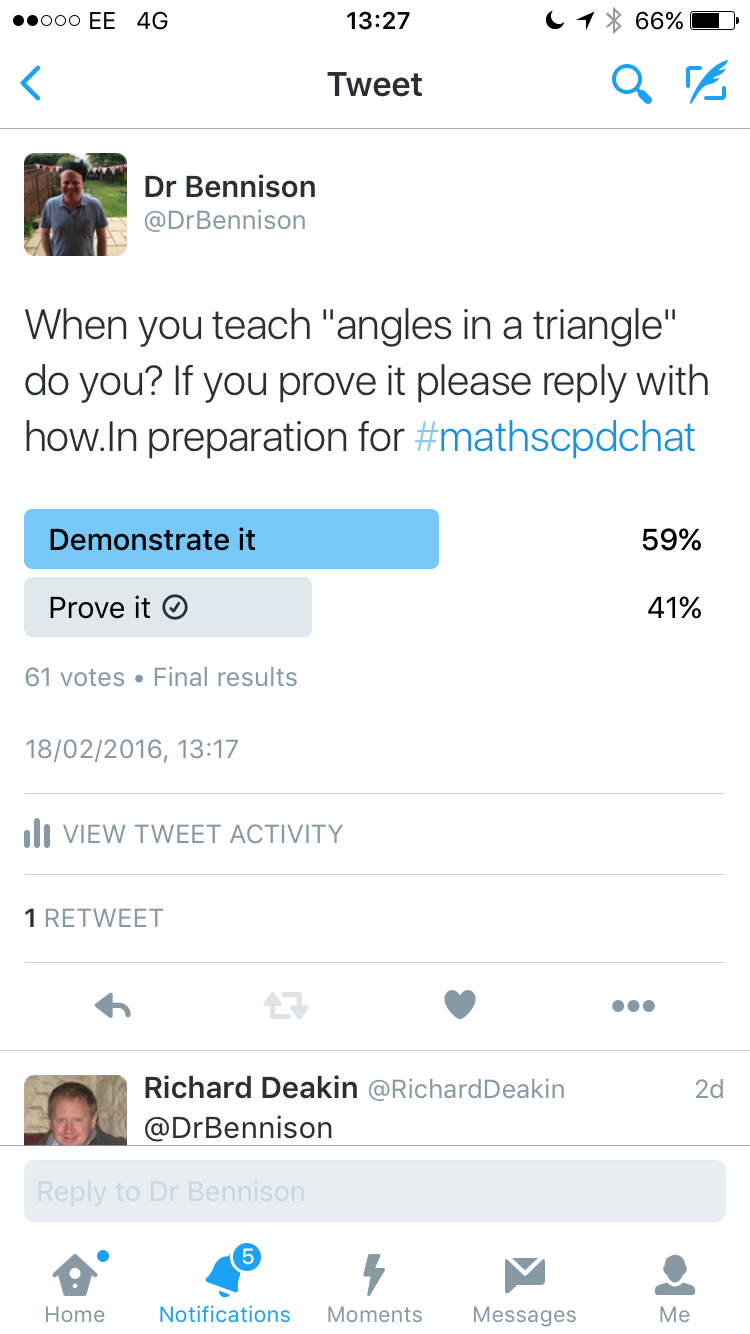
Last week I also ran a poll on twitter asking the question “When you teach ‘angles in a triangle’, do you demonstrate it or prove it? If you prove it please reply with how.” 61 people voted and the results are shown below.
To be honest I was a bit surprised by the outcome as I expected a significantly higher proportion of respondents to say that they proved it. Of course a demonstration of the result by either tearing the corners of a triangle and sticking them on a straight line or folding of the triangle is popular and a nice active way for students to visualise why the rule works. But one of the proofs is a classic application of the angle rules for parallel lines, as nicely demonstrated by Dawn (@mrsdenyer) on the back of an envelope, and so I expected a higher percentage of teachers to go through the formal proof with their students. 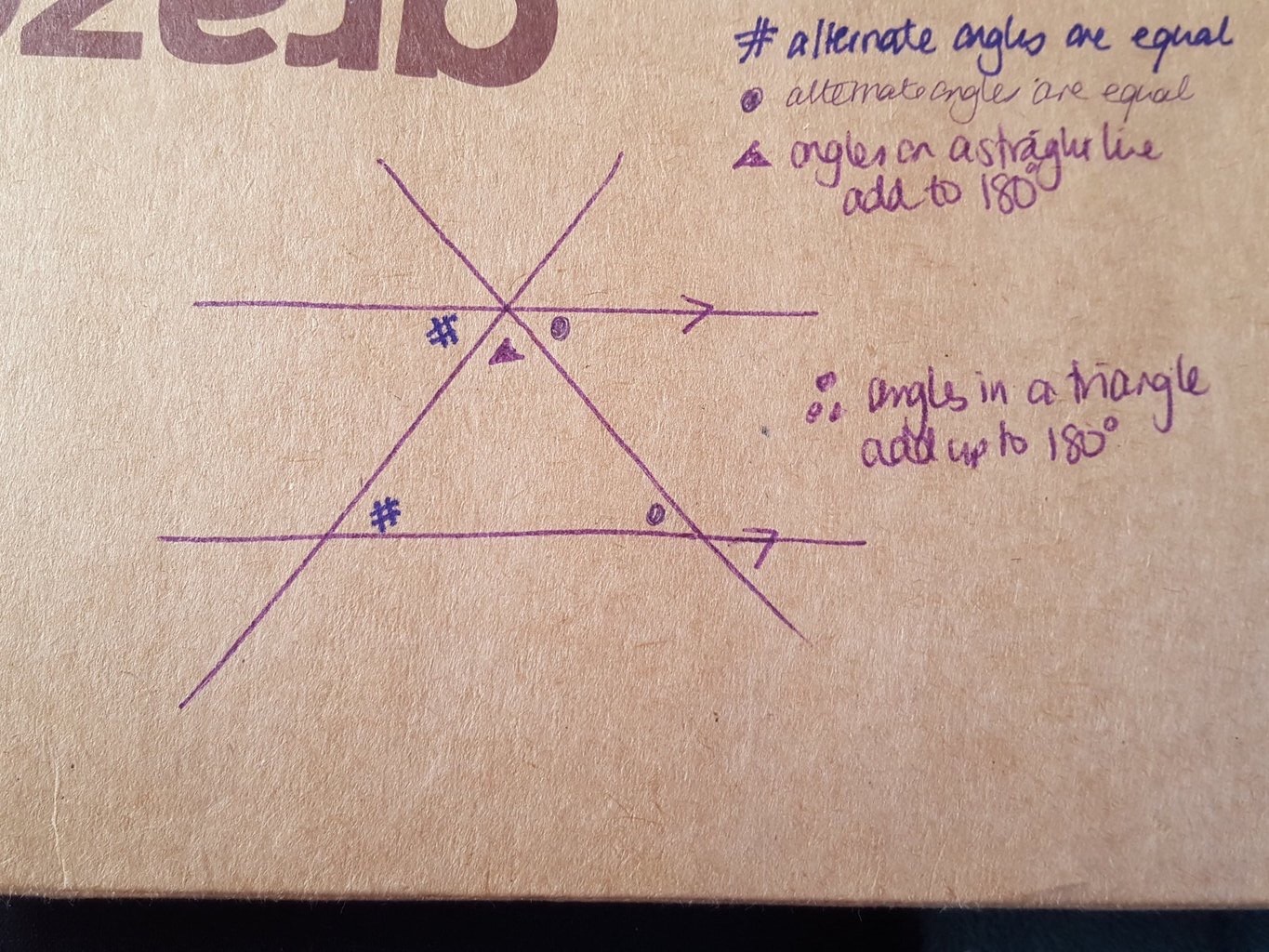
Some time ago Professor Smudge (@ProfSmudge) shared a file of proof questions that were used with year 10s in the “Longitudinal Proof Project” research study and I can remember being particularly struck by question 4:
This is a really nice collection of likely responses you would get in the classroom if you asked this question – Eric’s is particularly interesting as I can imagine many students being convinced by this because of its algebraic nature, despite being nonsense. I haven’t managed to find the time to read through all the reports from this research project and the subsequent “Proof Materials Project” which are all helpfully available online on the mathsmedicine website.
Finally, for tonight, Mark Greenaway (@suffolkmaths) shared with me a fantastic page on proof from his sufmolkmaths website which lists many activities designed to promote students thinking about proof, including this one from Mark Dawes about the prime numbers. Showing that all primes (greater than 3) must be of the form \(6n\pm1\) is a particularly nice thing to discuss with students as you can develop their thinking from an intuitive grasp of the result to a proof involving modulo arithmetic.
Anyway, enough of my rambling – I am looking forward to the discussion tomorrow.
One reply on “Proof at Secondary School”
Nice post, unfortunately I’m out tonight so.will miss the chat. I think some of the points your friends mention are good arguments for.splitting the maths GCSE into two – maths and numeracy