Merry Christmas to everyone reading this! I hope you have had a fantastic day whatever you have been doing.
In an effort to kick-start myself into blogging more I am aiming to post a blog post for each of the 12 days of Christmas. These posts will probably be quite short, some may be fairly random, some may contain teaching resources etc.
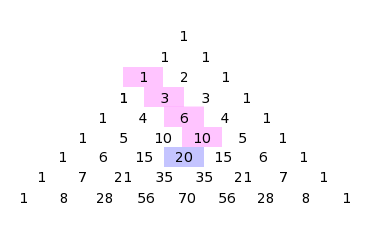
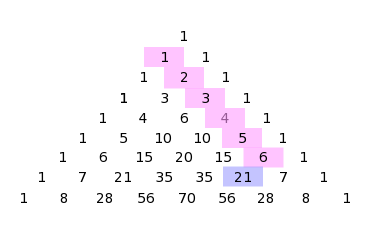
As it is Christmas day I thought I would write briefly about a Christmassy-themed theorem involving Pascal’s triangle. The so called, Christmas Stocking Theorem. I only came across this theorem a week ago when David Bedford (@DavidB52s) mentioned it…
This theorem states that a diagonal sum of \( k \) entires from Pascal’s triangle is equal to the entry below and to the left of the last diagonal entry in the sum
Mathematically this is equivalent to saying:
$$ \large \sum_{i=o}^{k-1} \begin{pmatrix} j+i \\ i \end{pmatrix} = \begin{pmatrix} j+k \\ k-1 \end{pmatrix} $$.
In the above, \(j\) tells you the row at which you begin, and \(k\) is how many entries you will sum. For example for the first picture above \(j = 2\) and \(k=4\), whereas for the second \(j=1\) and \(k=6\).
In future posts I may prove this in some fashion but I’ll leave you to experience the wonder for now….