Author: tombennison

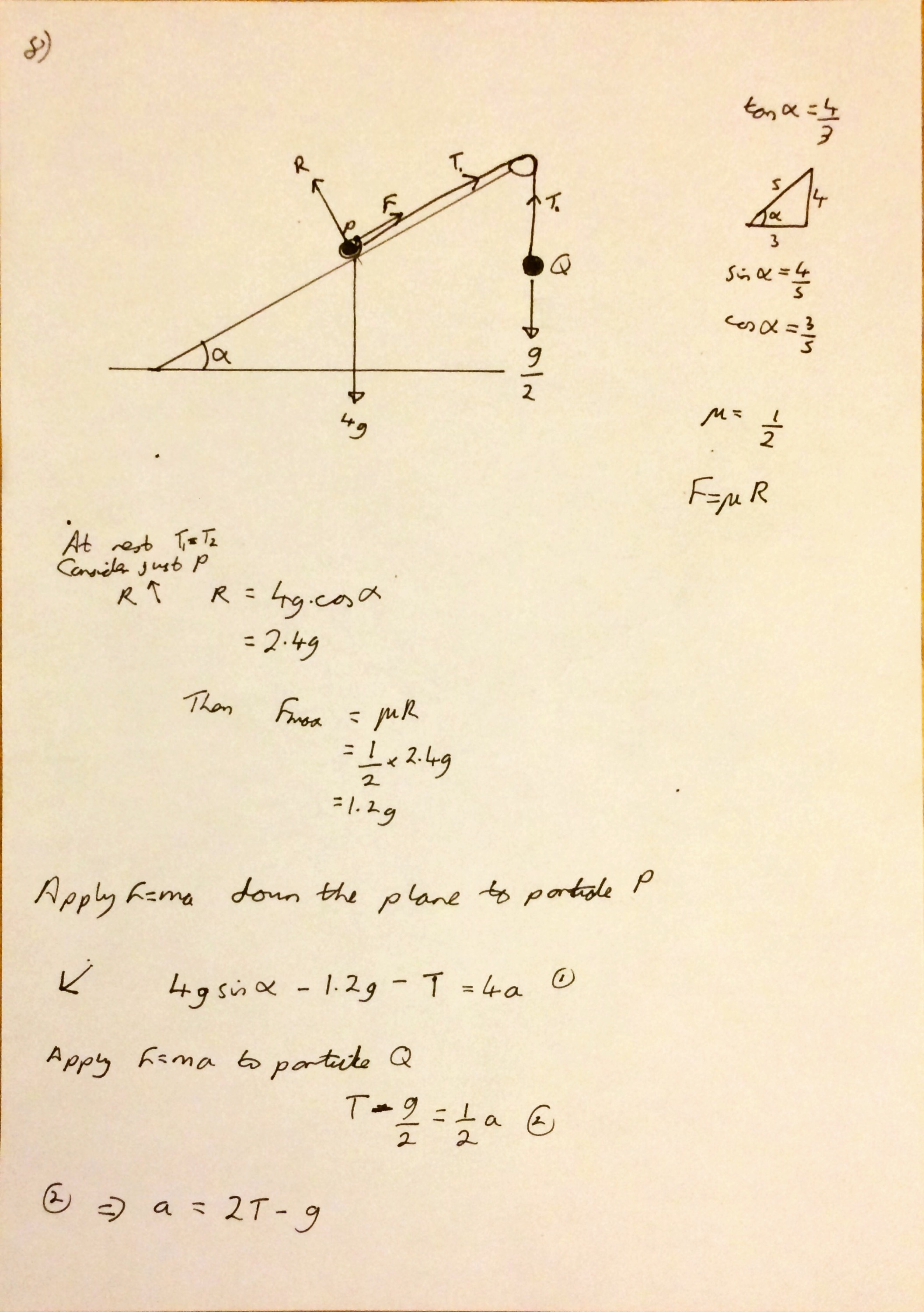
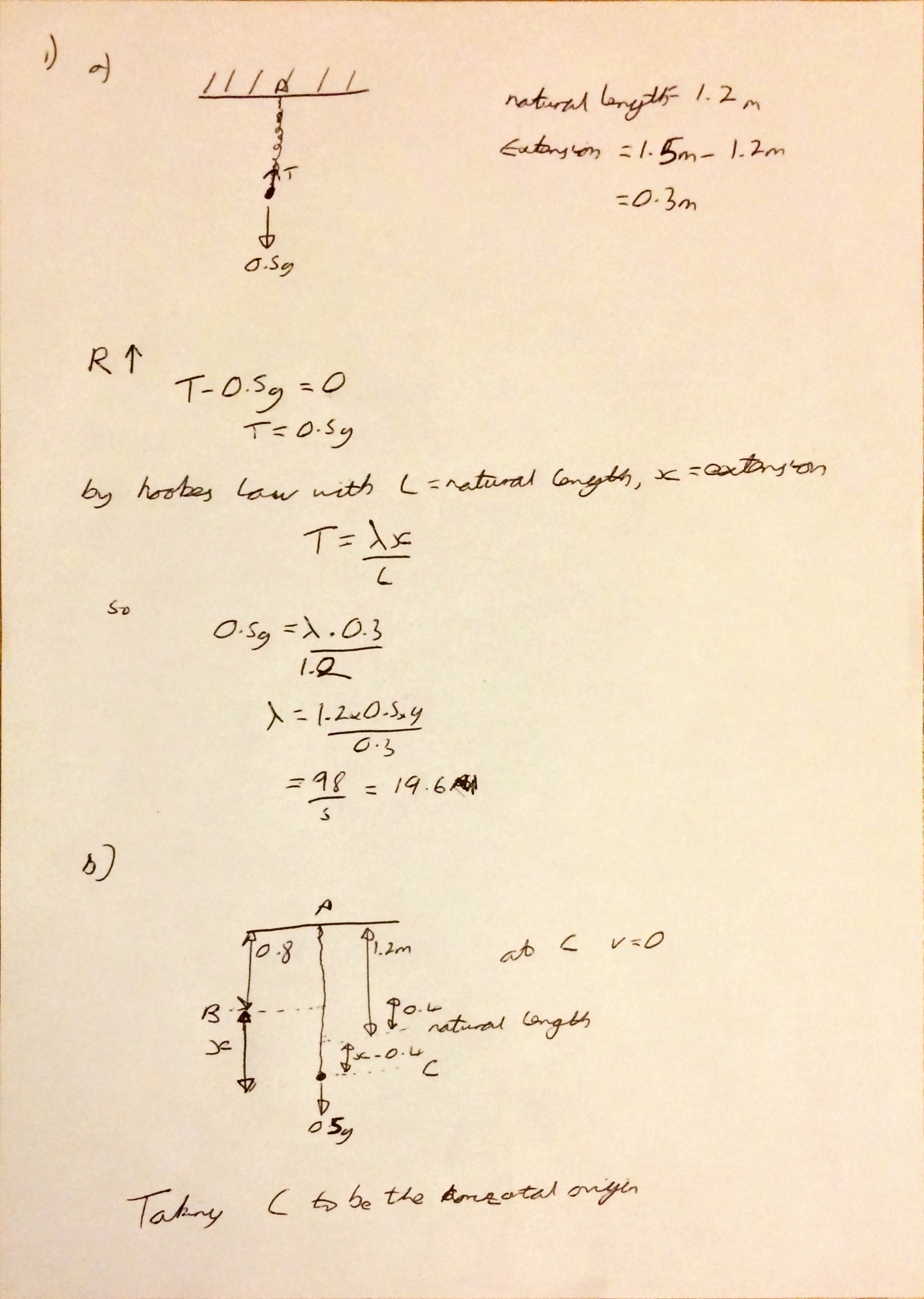
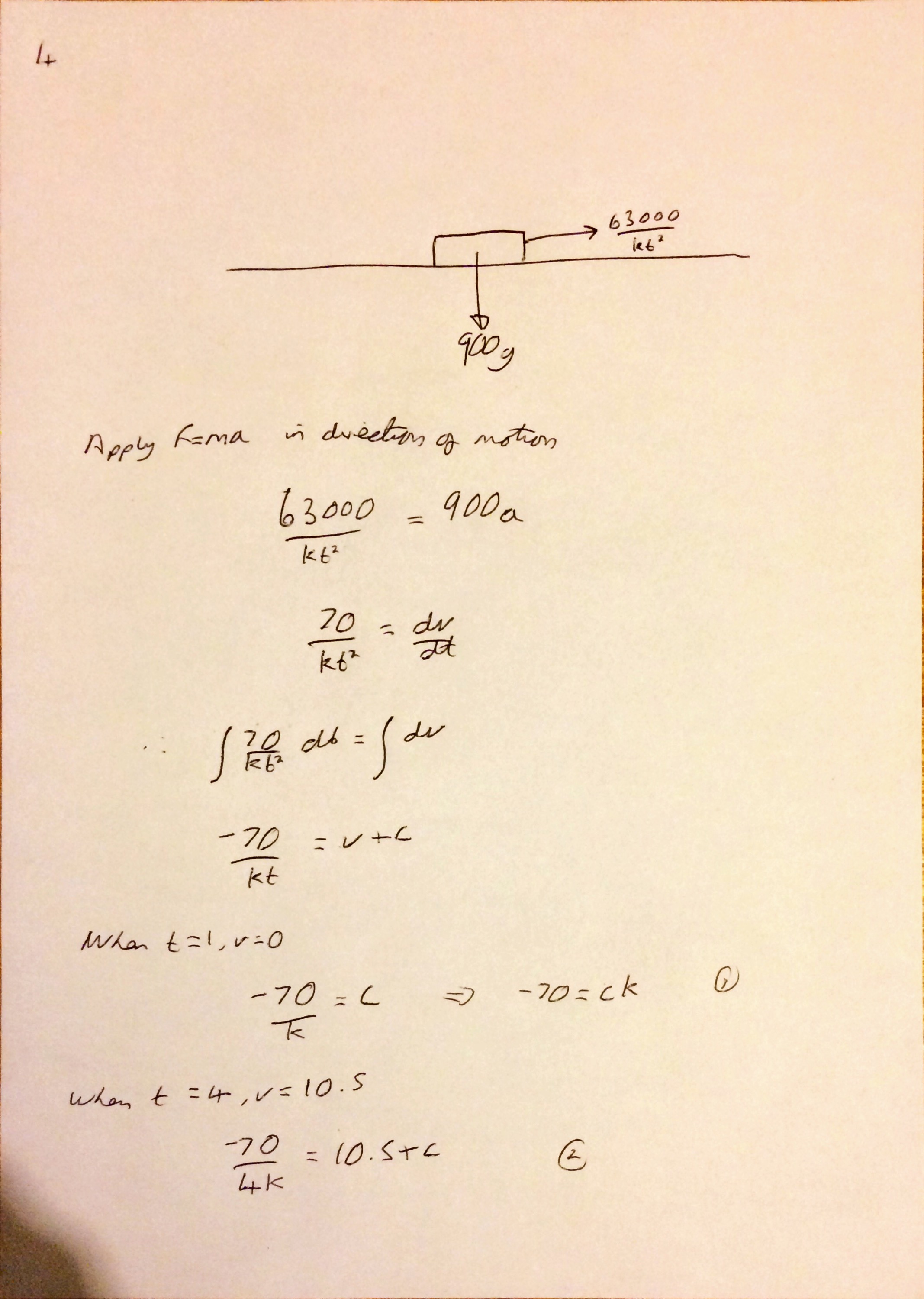
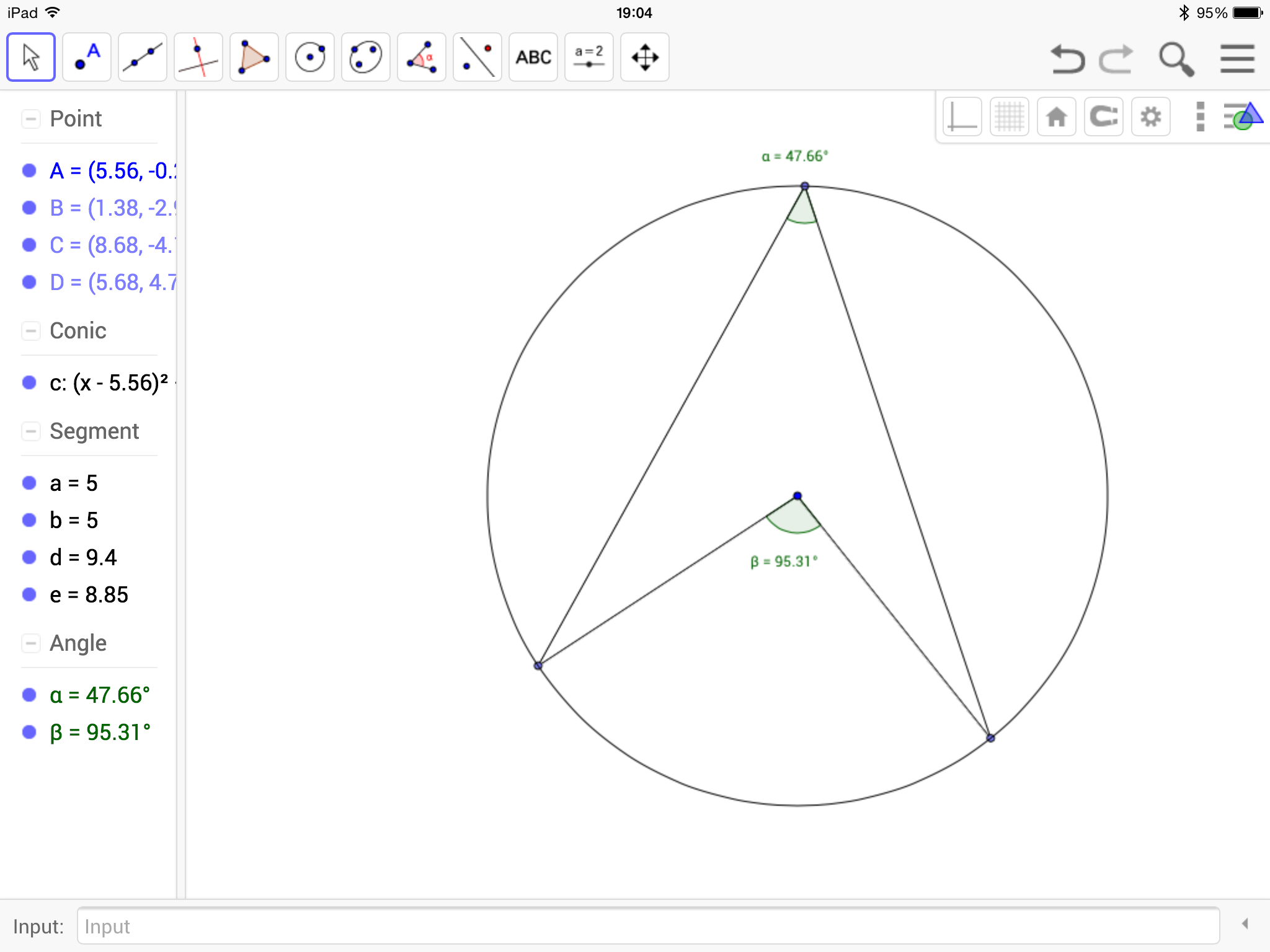
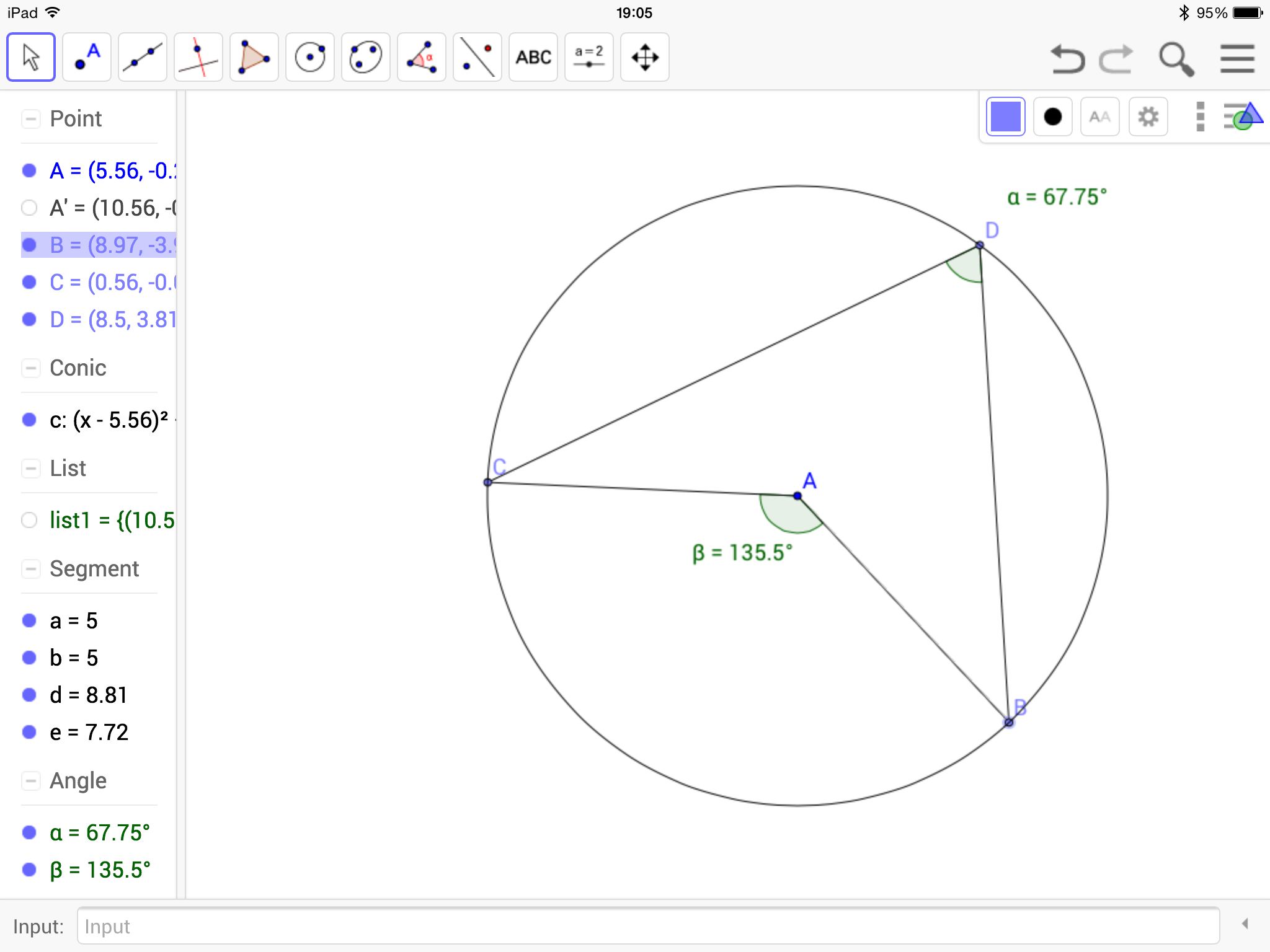
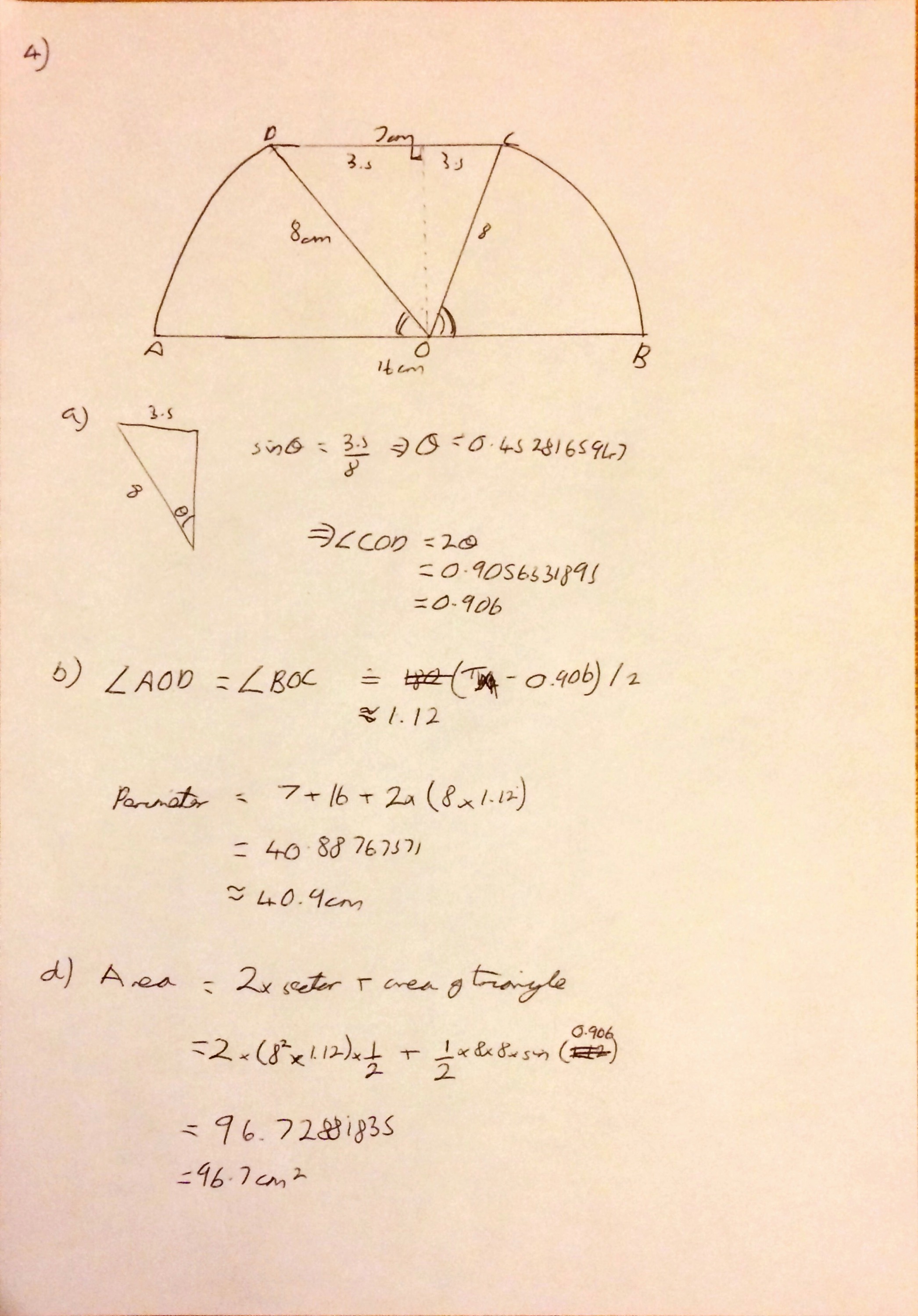
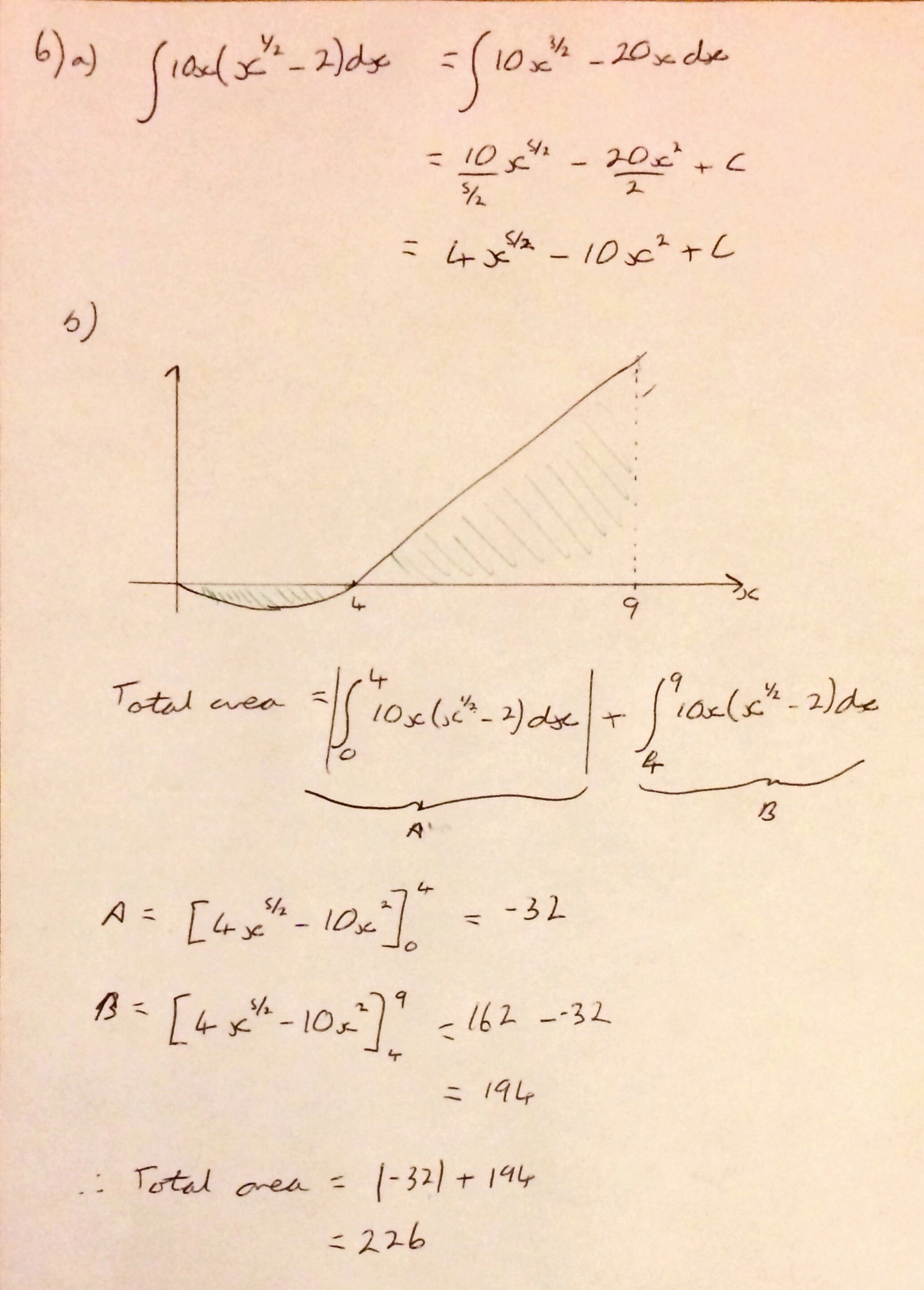
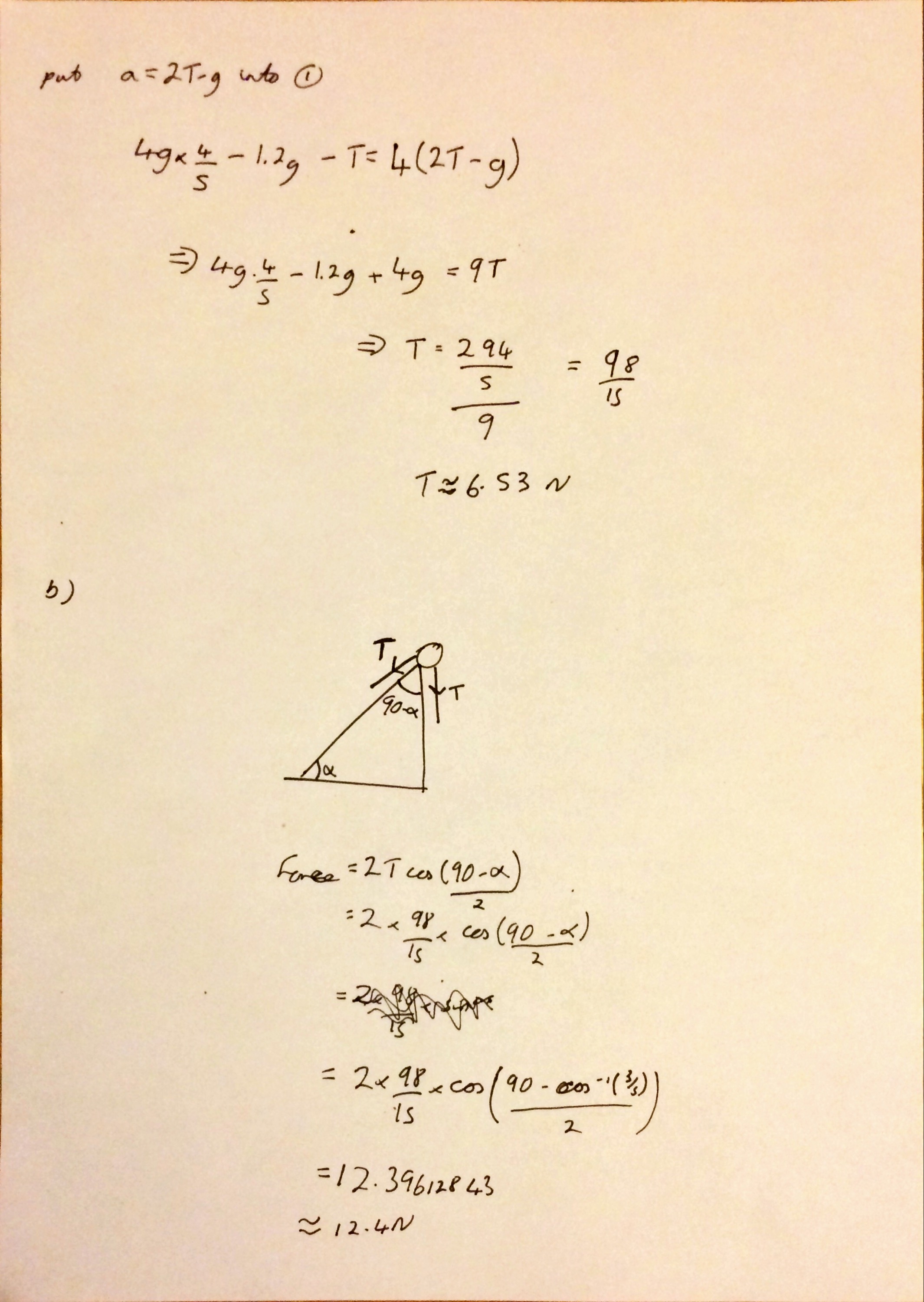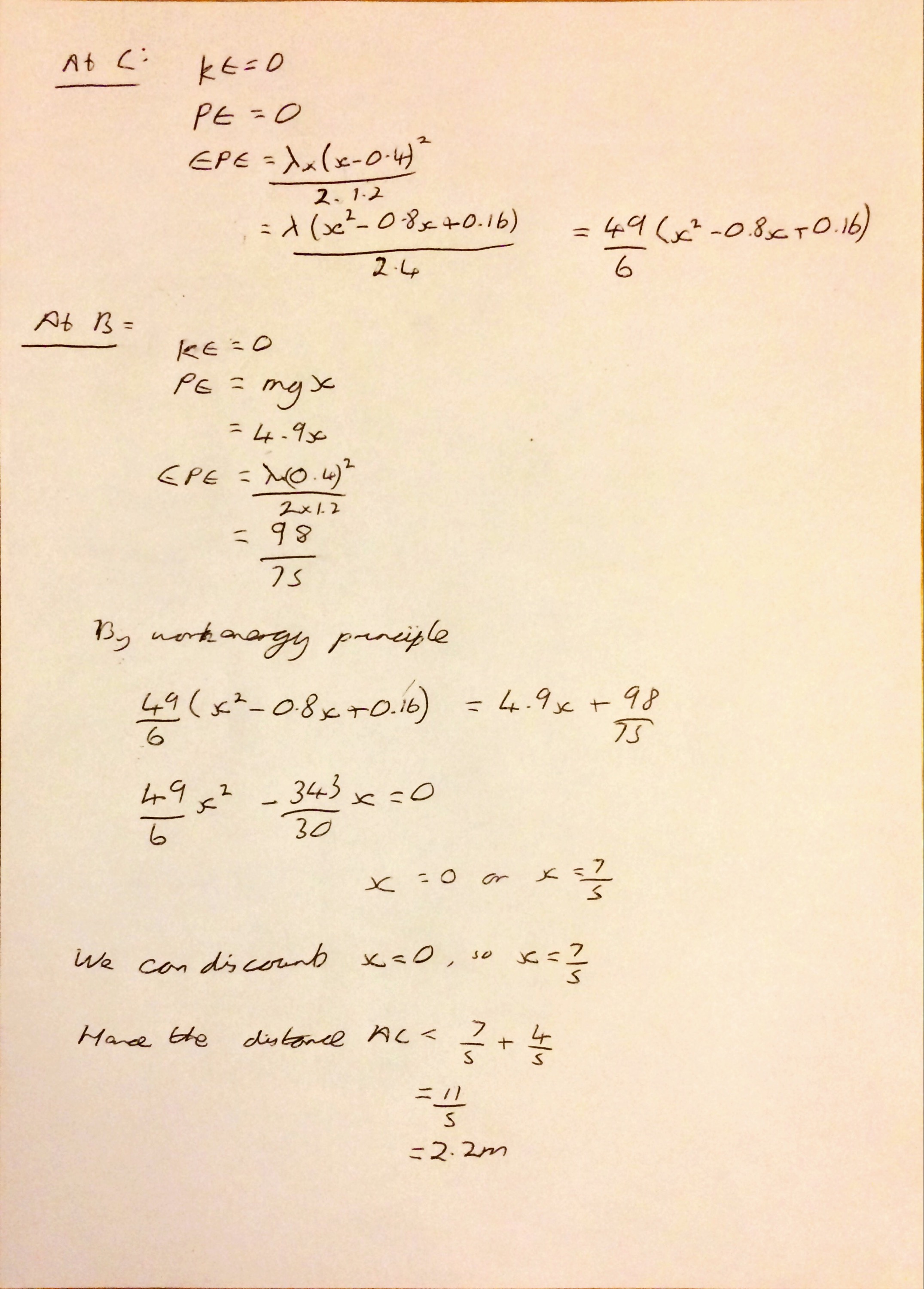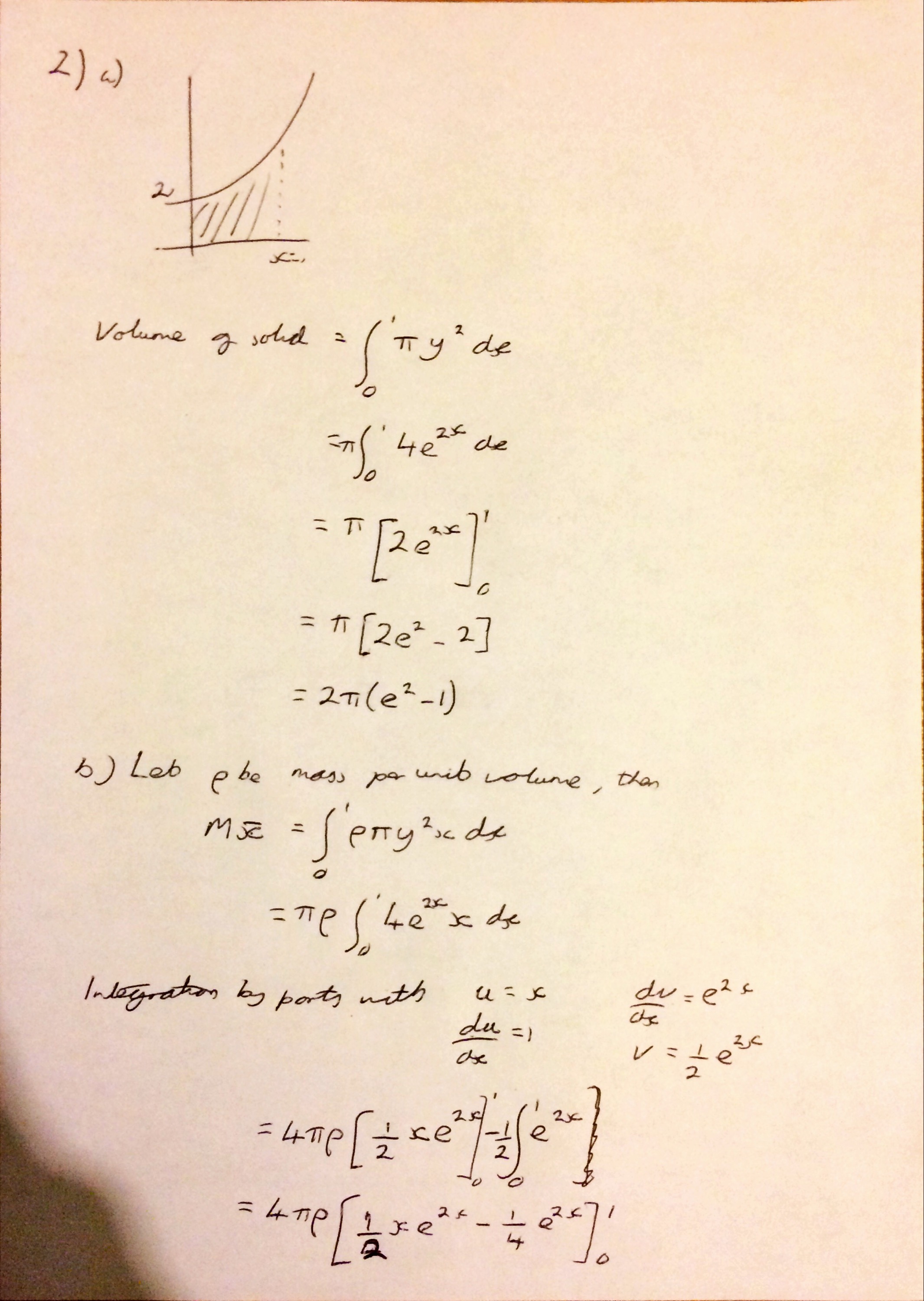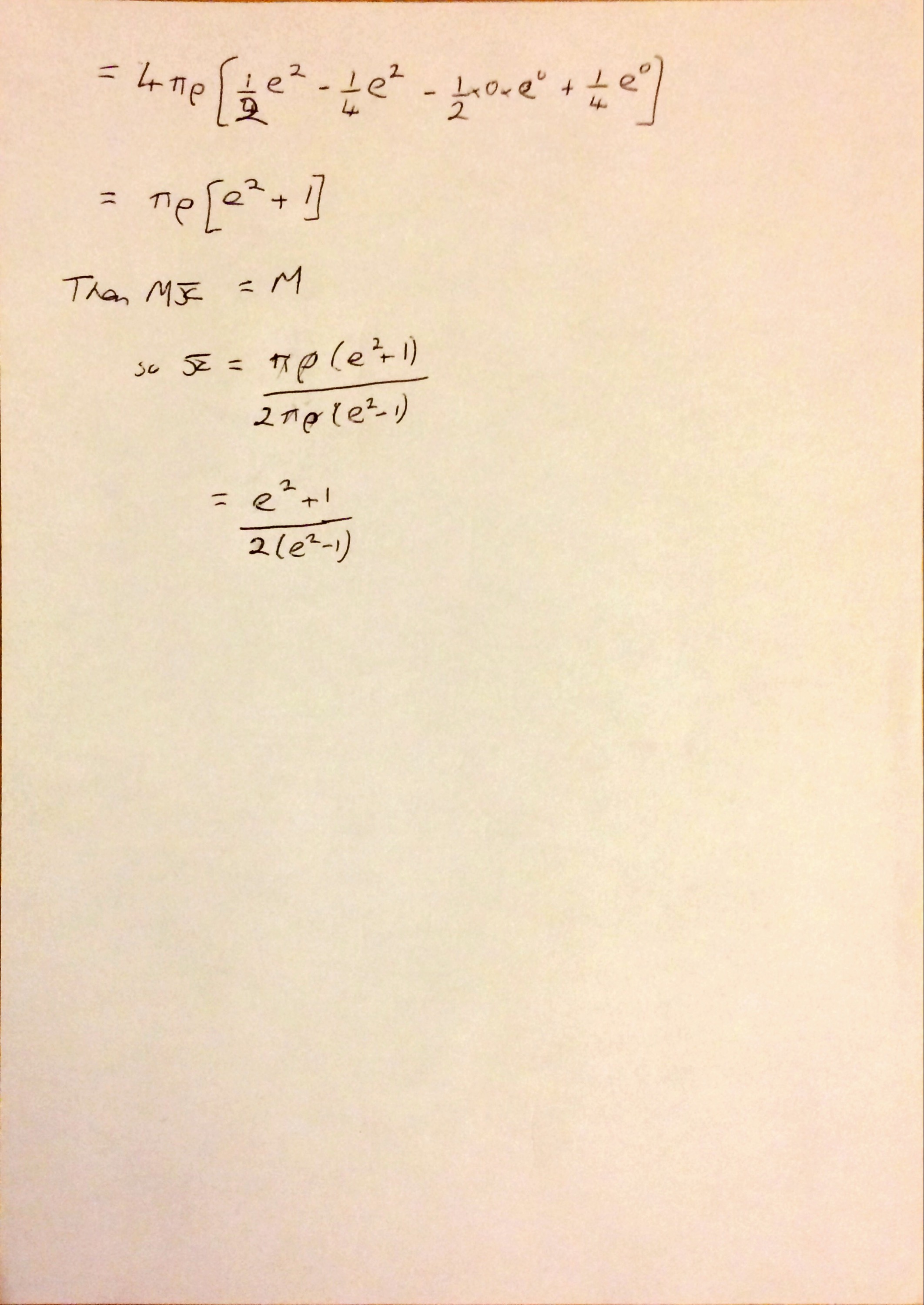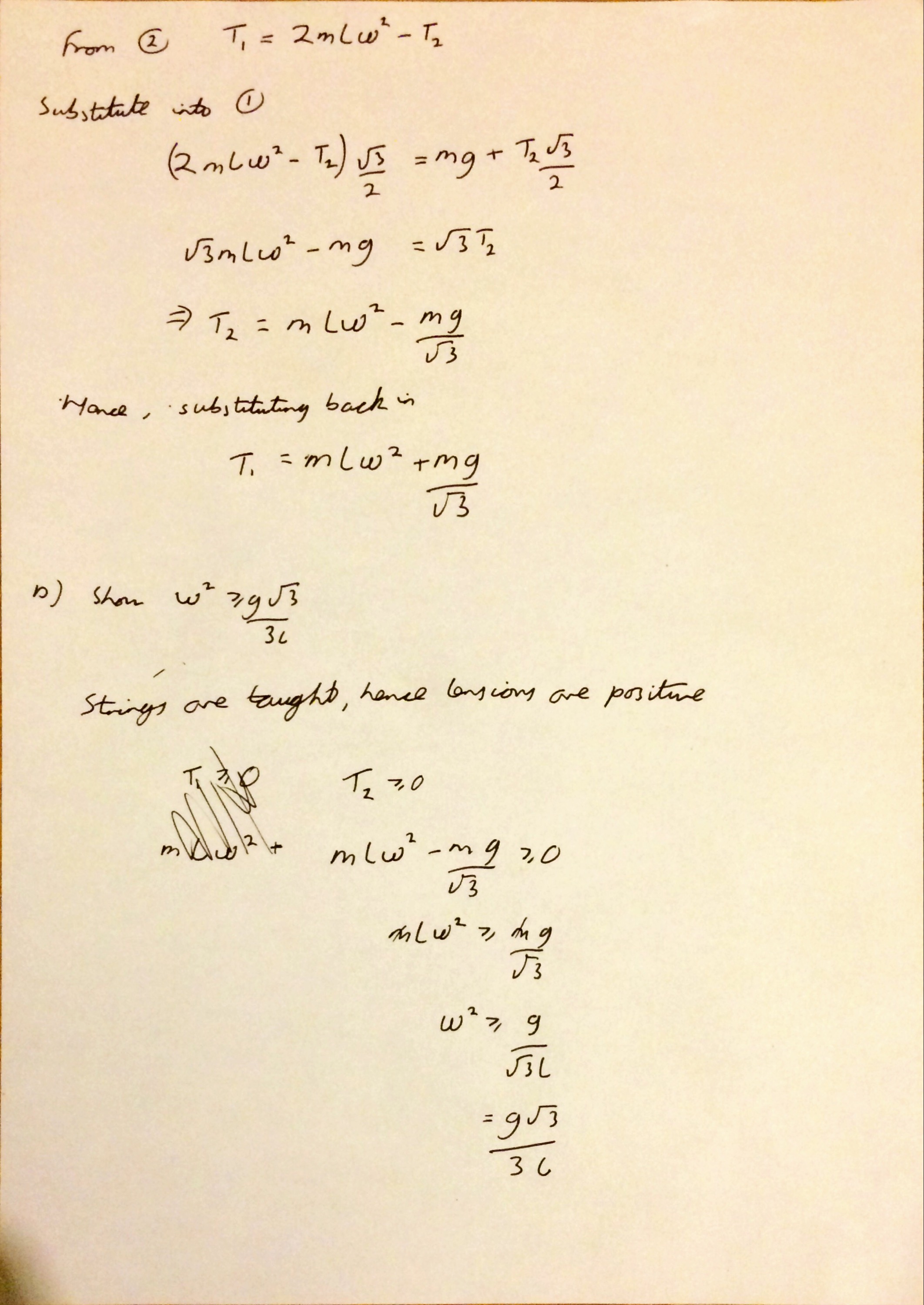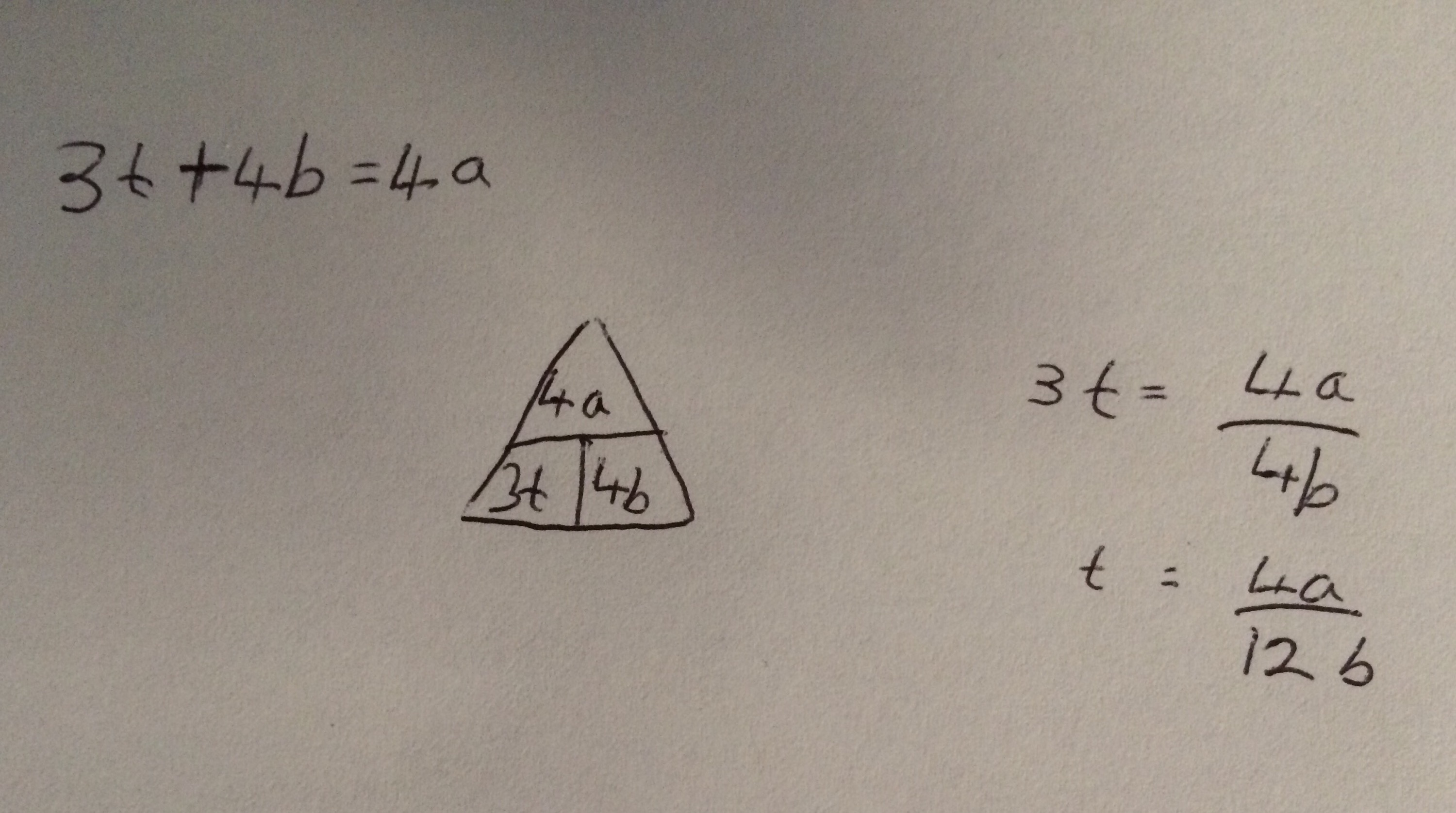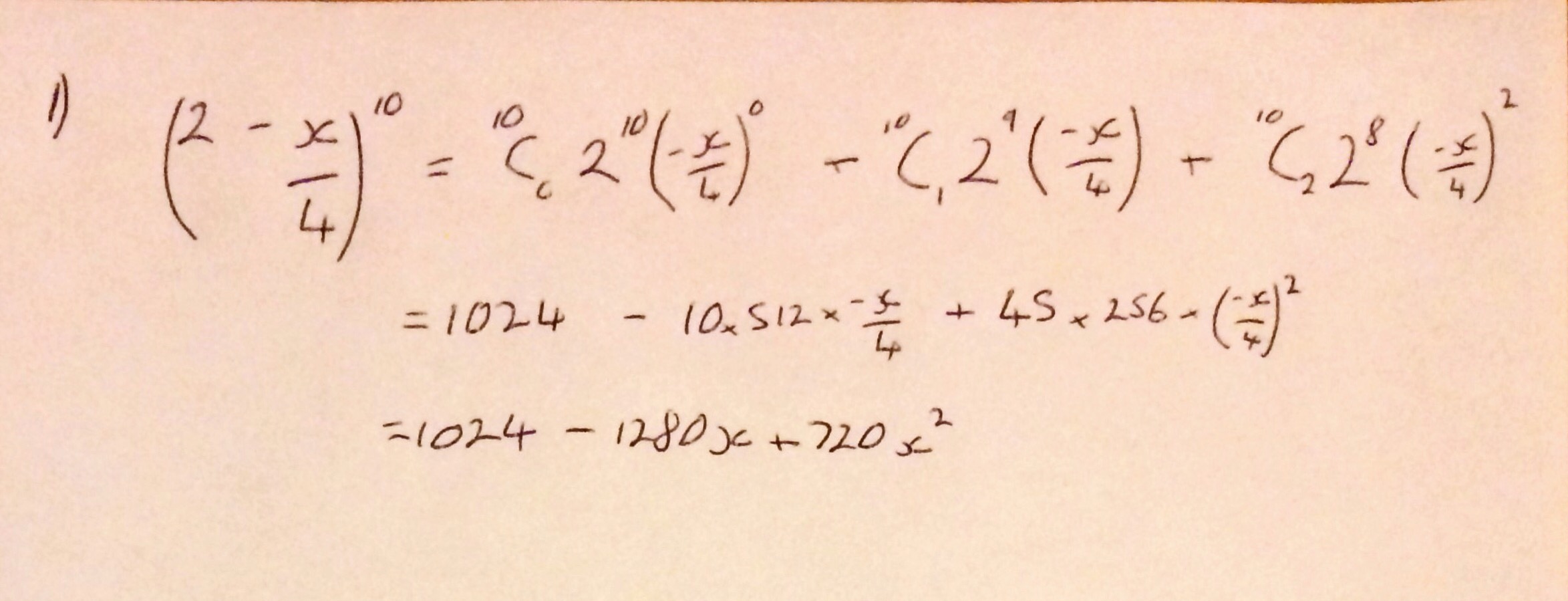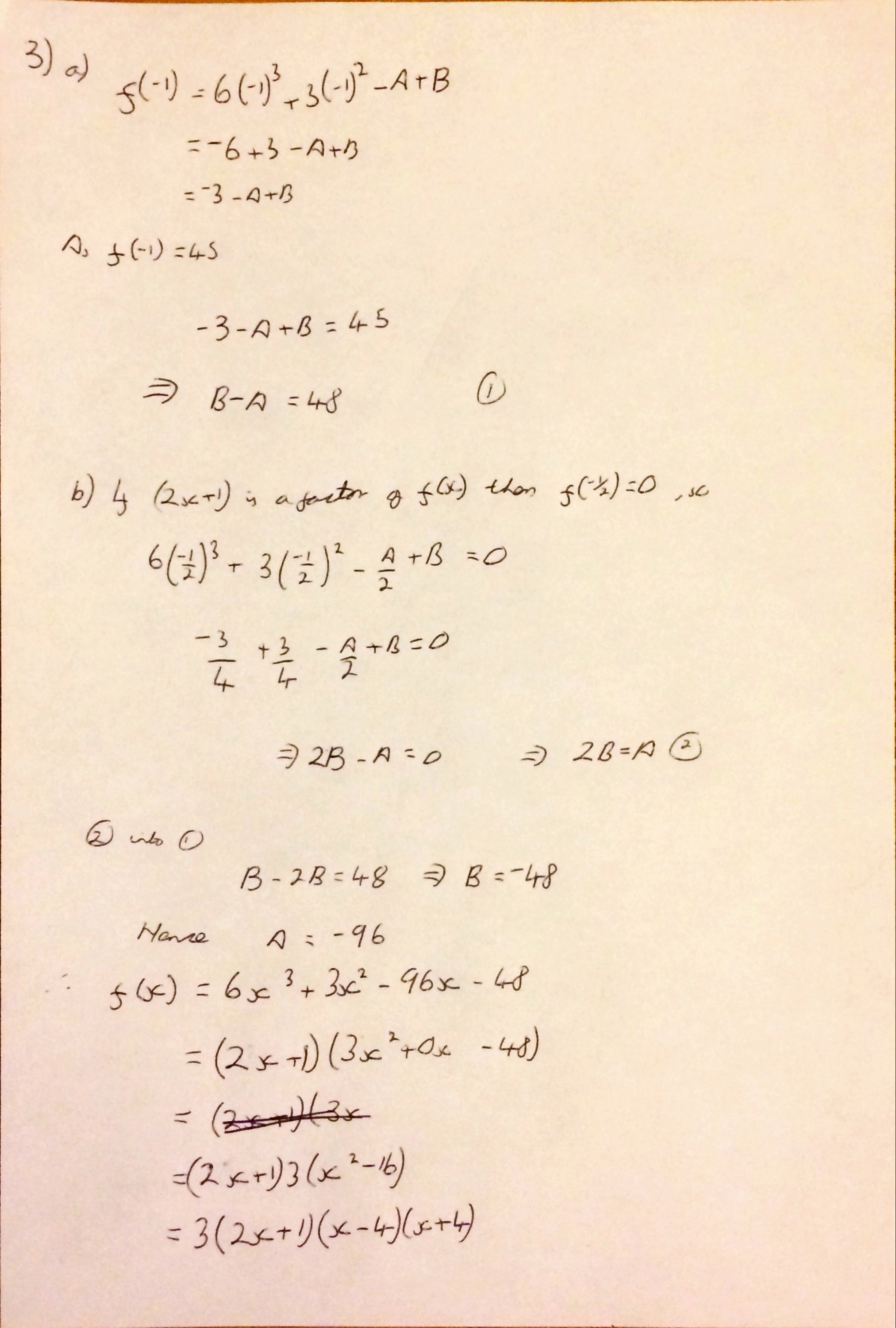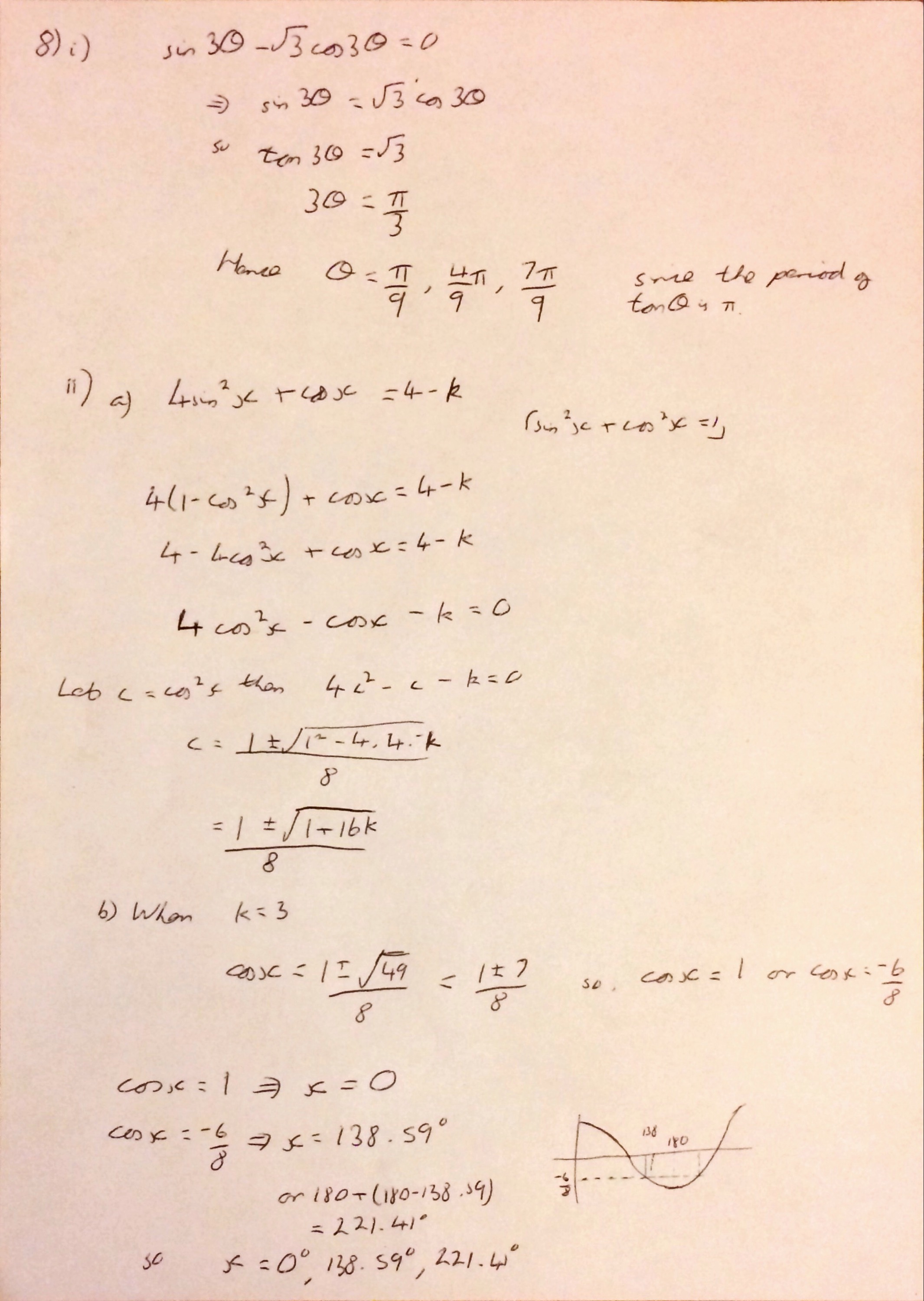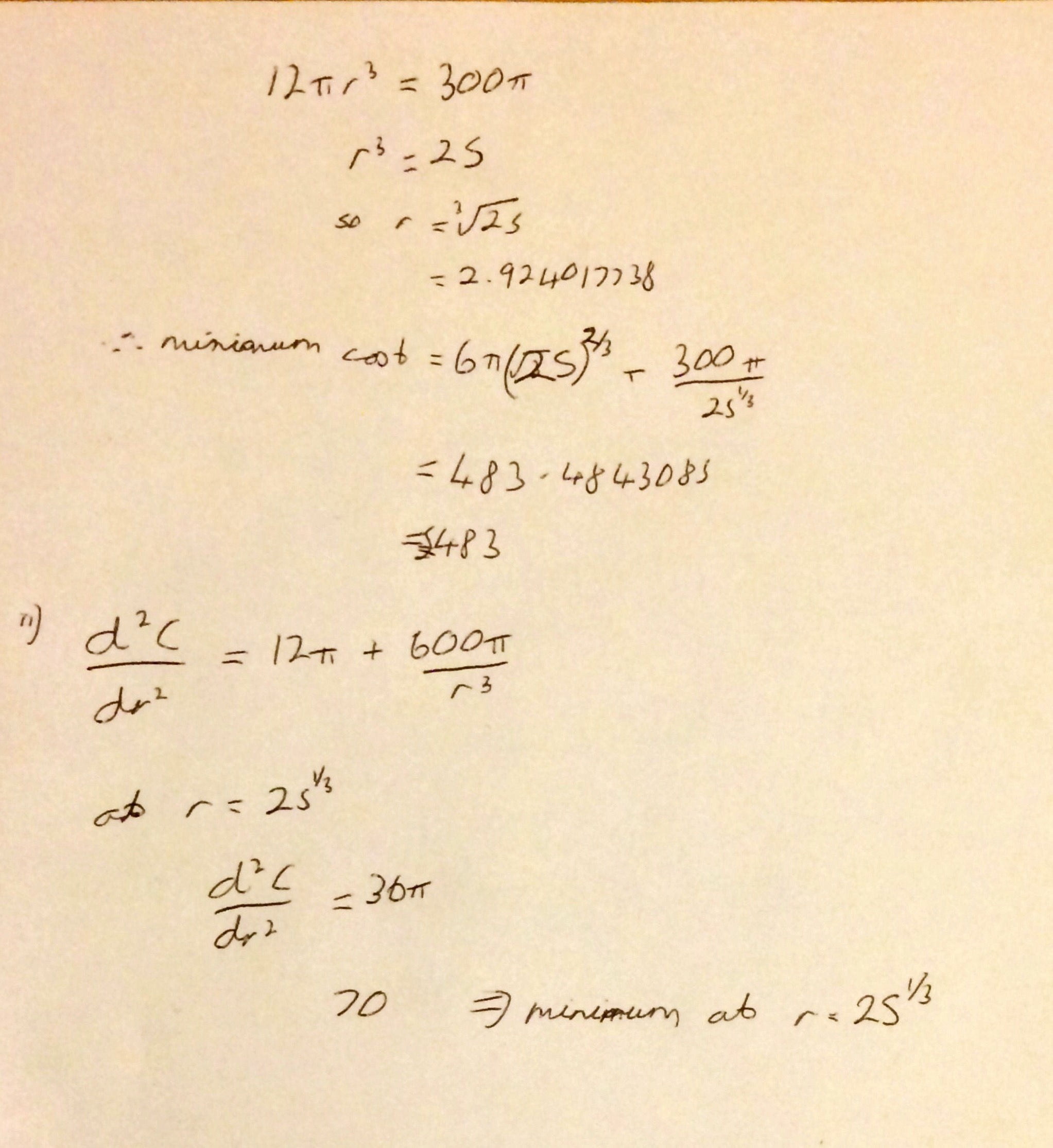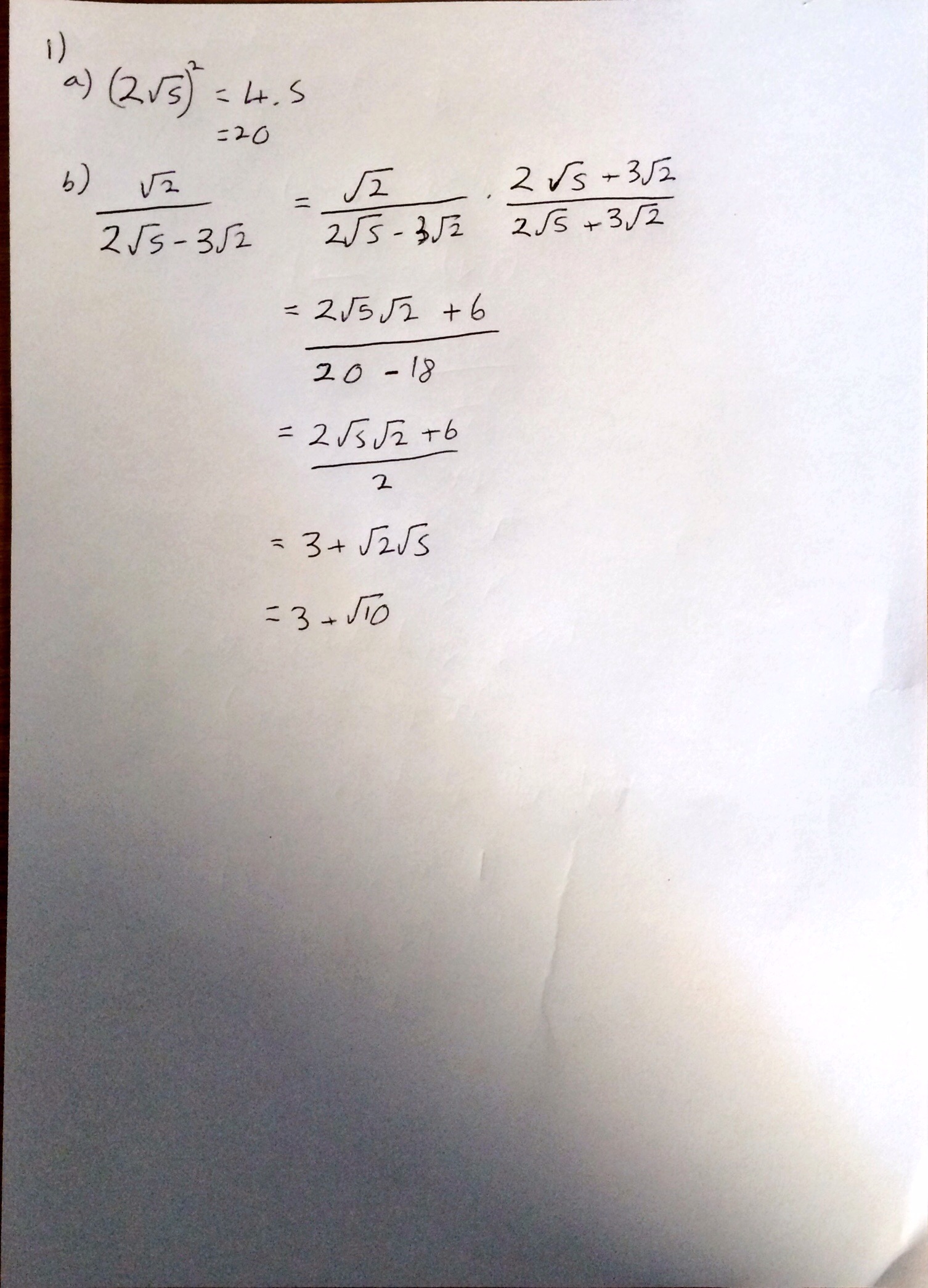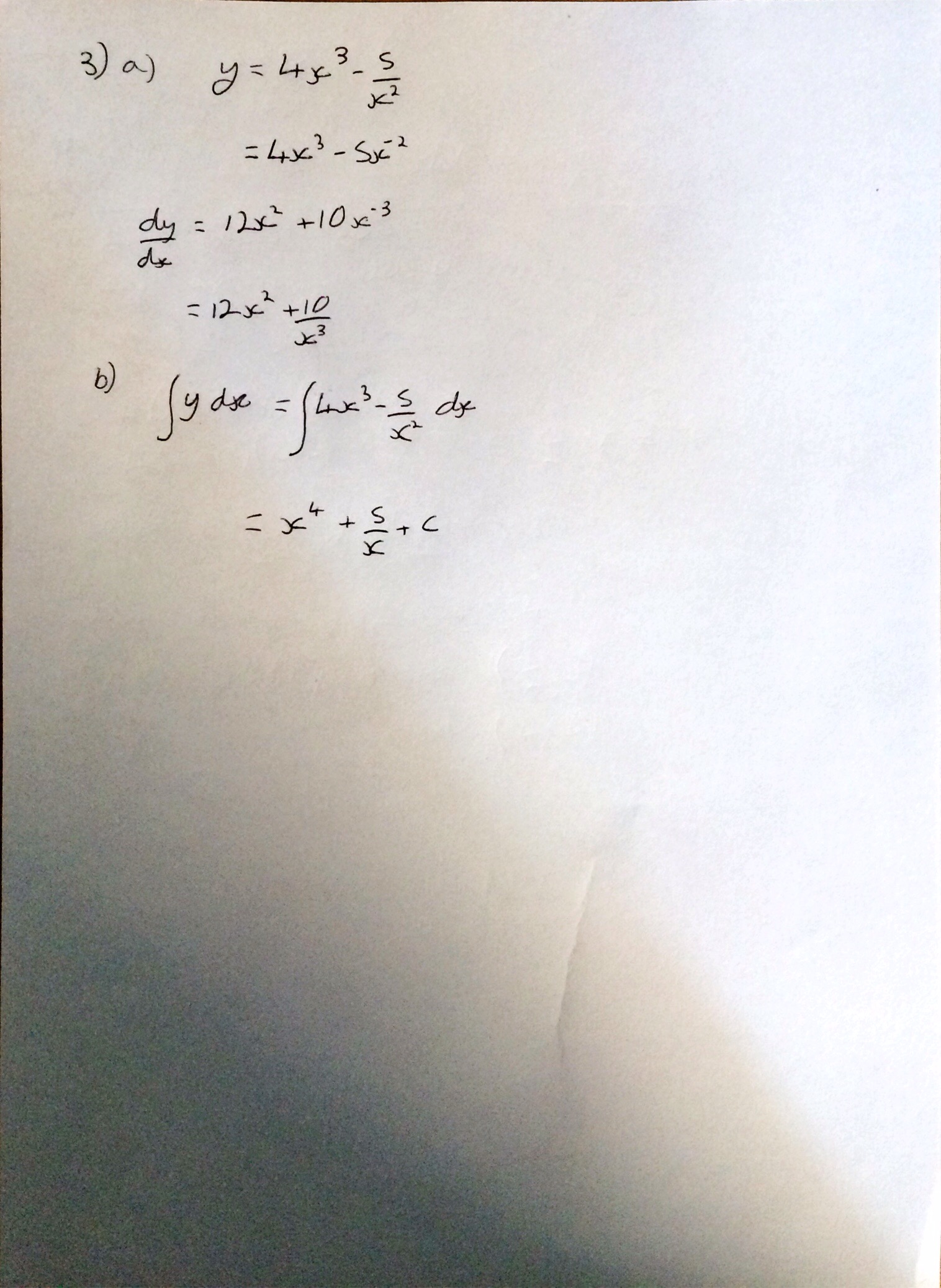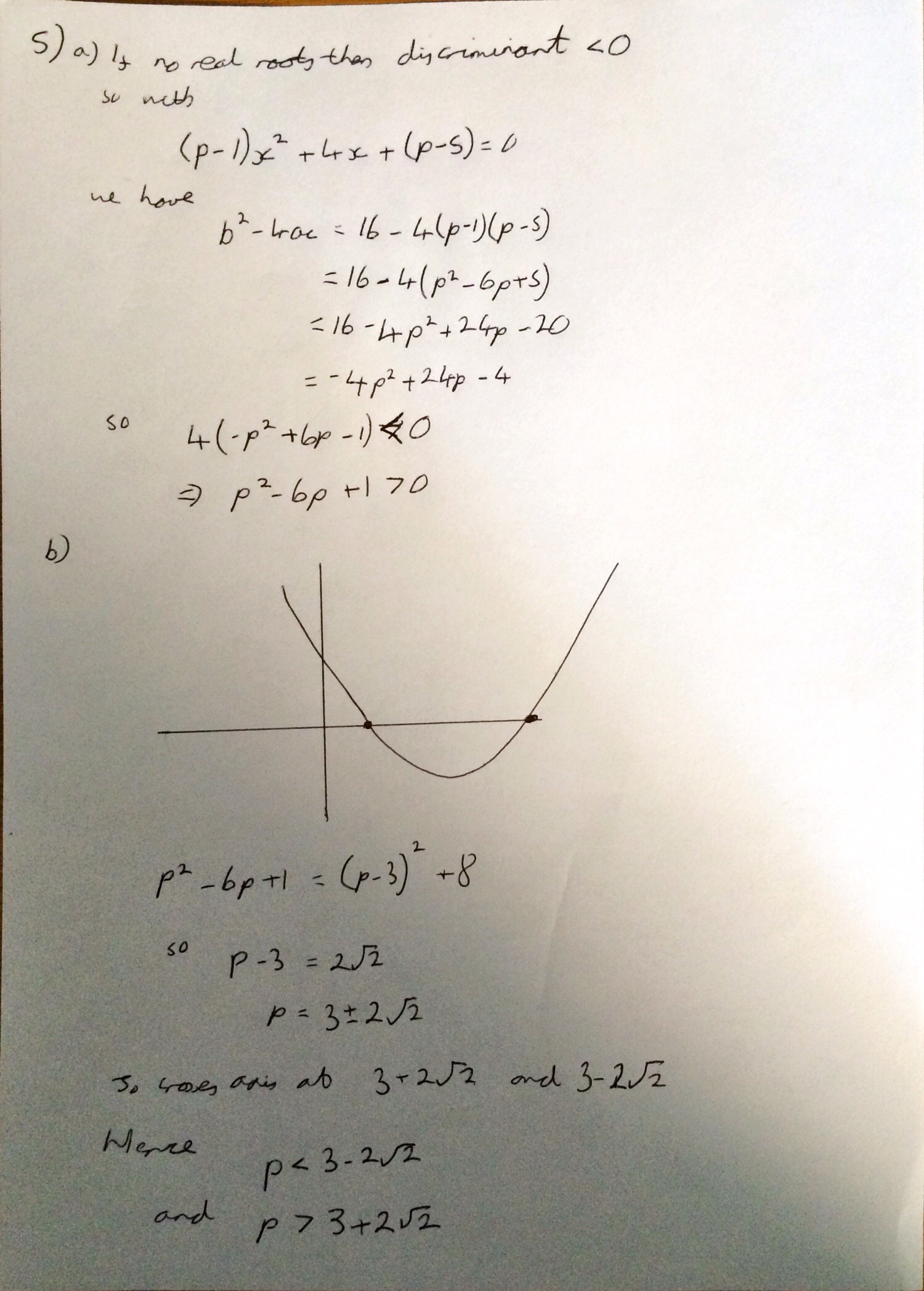I’m not sure why (someone probably asked me at school) but yesterday I started thinking about what I think leads to a good ethos in an A Level class and what I strive to achieve with my classes. 

My guiding principle with A Level groups is equality – I don’t want to be seen as a teacher who is above them. Real mathematics is a collaborative attack on problems where you are looking for an elegant, neat solution; this is hard to achieve amongst a group of people who don’t feel equal. I don’t want them to see me as a teacher above them who they can only ask questions of – I want them to suggest approaches and paths to the solution of problems too. I think one of the easiest ways to encourage this is to let them call me by my first name. I know some teachers wouldn’t like this, and it is of course important to keep a professional distance from your students, but, I really think little things like this encourage them to be comfortable to give me their thoughts and suggest ways to tackle a question that they are doing as a class. 

Another thing that I think is important for an A Level group to understand is the necessity to be stuck. In a Further Maths group especially some of the students have probably never struggled with maths before and it can be a shock when they begin to. For this reason I try to emphasise in the first few weeks that this is ok and a normal part of doing mathematics. Problems which either can’t be solved, or can be solved in multiple approaches, one of which takes significantly longer than another approach are valuable to reinforce that being stuck is ok! I also use exercises that I haven’t looked at until I get into the room as examples for this reason – I believe it’s good for them to see that I don’t always do the correct thing first time when solving a problem. 

Collaborative working is something that I try to foster with certain activities – certainly for me, maths at A Level was a very solitary activity. This isn’t really reflective of the world of mathematics and whilst it is important for students to have plenty of  practice at solving questions on their own, talking about and discussing mathematics is incredibly valuable. 

This post is a work in progress and I’m going to add to it as I think of other things….. 

I don’t think anyone in the UK can have missed the media frenzy over the first Edexcel maths GCSE paper of this year. For example see here and here.

Having done the paper I don’t think it was particularly unfair or hard. There were plenty of standard, well trodden questions aimed at the C/B range. The questions targeting students looking for an A or A* are designed to stretch the most able and should be hard. I think there was a clear change in how se of these questions were written and I suspect this is a reflection of questions to come with the new GCSE. 

One of the questions that has gone viral is the “Hannah’s Sweets” question  

 

Apart from the pseudo-context (I don’t see how you could know this probability without knowing how many sweets we’re in the bag to begin with) I quite like this question. It brings together probability and algebra, using algebra as it was designed – a tool for solving problems. In fact, as long as a student writes out what they know from the question it is in fact fairly easy. At A Level I emphasise writing out what you know from a question if you don’t know where to start, but in the past I haven’t really done this to the same extent with my GCSE classes. 

This question, however, is unlike any of the probability questions on recent year’s past papers and this is, I think, where the problem lies. I try not to teach to the test, but the fact that some of my students struggled with this question shows (depressingly) that to some extent I do. A lot of my revision lessons, probably like most teachers, have focussed on past paper questions as a way to prepare students – for this question this approach has failed. 

From what I remember in one of the new specimen assessment materials there is a tough looking probability question involving a spinner similar to this… To prepare our students for these new exams I think I am going to need to change how I do exam preparation at GCSE. I don’t think this is necessarily a bad thing, maths is a problem solving tool, students shouldn’t just be expecting to see the same style questions year in, year out. I suspect that past papers for the new GCSE won’t be able to be used to coach pupils into the question style, at least not for the high attaining questions. 

This is a good thing in my opinion, but my main concern though is the time necessary to build this deep understanding, especially for the first couple of cohorts for the new papers who won’t have had the required preparation at Key Stage 3. For The new Year 7 we are going down the mastery route and this should allow us the time to build this deep conceptual grasp of topics and how they inter-relate which will be good. 

Going back to this year’s Paper 1 another question that a lot of my students were talking about was the “conical grain store” question. I loved this question, nice numbers to work with and it essentially boils down to a pair of simultaneous equations to solve using substitution. Substitution is a method that in hindsight, I strangely down do enough of at GCSE, but would use almost exclusively with an A Level group. The question concerning the perimeter of a shape made up of 4 congruent triangles and 4 congruent rectangles was also nice – just Pythagoras in disguise. I’d wager a bet though that a large portion of students didn’t even attempt these questions due to the unfamiliar context. 

All in all I think it was a completely fair paper, and I’m looking forward to seeing tomorrow mornings paper. I wonder if there will be another Twitter frenzy…. 

Update: Ed at Solvenymaths (@solvemymaths) has written a fantastic post with some thoughts on how to address the gap between current student’s problem solving skills and what will be required for the new style GCSE questions. 

Yesterday morning students at my school sat M1, FP2 and the OCR FMSQ papers. This is the first of three posts looking at these papers and I’ll start with the Mechanics paper. 

I’ll admit I’m feeling pretty tired at the moment and so I made a few mistakes that I had to correct as I went through the paper – have fun spotting them. Overall I think it was a standard M1 paper which included the obligatory question using a 3-4-5 triangle. 

Question 1 was a very straight forward conservation of momentum question – as long as you don’t get confused with the direction the particles are moving in there are easy marks to get here.  

 

I thought that the projectiles question on this paper (Question 2) was really nice; no projection at an angle, just straightforward motion under gravity. Nice numbers too so that the arithmetic was relatively easy. The last part of this question was straightforward, though I can see some people working out the time to get from 14.7m to 19.6m and then the time back down instead of using symmetry.  

 

My students commented on how Question 3 was nice as you got 7 marks for just resolving in two directions. A very simple question really as long as you are confident with solving simultaneous equations. 

 

The first question that I made an elementary mistake on was Question 4. This year ion concerned a lift inside of which was a crate. If you recognise when to consider the motion of the system and the crate separately it is pretty easy. However, when I district did it and considered the motion of the lift-crate system I included the normal reaction of the crate in my force balance – very silly of me.  

 

Question 5 was a typical moments question with a bar suspended from the ceiling and with particles suspended from it.  Taking moments about two points allows you to easily find the tension in the ropes for the first part. The second part is marginally trickier as you need to have an understanding of how the rod would move if the particle was changed. 

     

Question 6 part a seems hardly worth asking as a distinct question, but I guess it is only worth one mark. I have also realised I did part c in a much more complicated way than necessary 🙁 

 

I found question 7 strange as I realised that I had worked out most of part b as I drew the graph. So maybe it is only the shape of the graph and the relative gradients of the acceleration and deceleration that they are looking for in the mark scheme of the first part        . Finding V for the final part of the question is straight forward given the stepping stones you are led through in part b. 

 

Overall I liked the final question. However, I remember that when I did my A Levels finding the resultant force exerted by a string on the pulley was something that I struggled with. Indeed this is the part of the paper that most of my students said they struggled with. They also all said they were surprised that the first part of this question was worth 11 marks.  I agree I think, it could easily have been worth less marks so it’s quite a nice question to end the paper on I think 

   

I’d be interested to know what you or your students thought of the paper….

Yesterday I was pleased to notice that the packaging for the new recipe flavoured milks includes some nice maths puzzles on three of the four varieties (only the chocolate fudge flavour doesn’t contain a number Puzzle)  

   
 

I think these are pretty nice for their target audience – which I guess is a lot younger than me!! 

Go on, spend a minute and give them a go 😉

Next year I am likely to be teaching Mechanics 3 to my further mathematicians and so I thought I should have a go at this years exam paper (1 person sat it at school so I had a copy of it). After seeing this video I was a little nervous as I hadn’t looked at this since I did my A Levels, however I didn’t find it too bad with a bit of help from my old A Level textbook:

   
Question 1 I thought was pretty straightforward – once I had refreshed my memory of how to calculate elastic potential energy it was just an energy conservation question. Please excuse that I have written Hooke without a capital letter.

Question 2 was nice, as long as you could remember how to find volumes of revolution, and then use this to find \(\bar{x}\)

  

  

For Question 3 I realised that sometimes I have no intuition with the mechanics questions. Even though it was asking you to find the tensions in each string I still expected them to come out equally – of course in hindsight this clearly wouldn’t have made much sense. The circular motion stuff came back to me quicker than I expected to be honest, and this question dropped out quite nicely. 

   

Question 4 was a nice power type question, I thought it was very like an M2 question, just with the complication of non constant acceleration. I really like how the question required you to use the Trapezium rule. As a numerics guy I think how the numerical methods are presented at A Level is incredibly sad. The trapezium rule is great, and it could be used so much in the applied modules – students wouldn’t like being asked to use something from Core 2 in other modules though. I think I may have to write about the Trapezium rule……   

 

Question 5 is a nice centres of mass of a 3D solid. It considers a spindle formed of two cones. In hindsight it would have made more sense for me to work out the Center of mass using moments from A instead of taking moments from B

   

I can remember loving questions like Question 6 when I did A level, and I still quite enjoy showing that a particle connected to two springs exhibits simple harmonic motion. Like many questions as long as you are comfortable with applying F=ma and solving simultaneous equations it is fairly straight forward. 

     

The final question considers a particle moving on the surface of a sphere and uses conservation of energy and F=ma. I wouldn’t be surprised if some students forgot to add the horizontal distance moved whilst on the sphere in the final part.   

     

Formula triangles are quite prevalent in the UK (I’m not about elsewhere to be honest) – especially in science lessons and when right angled triangle trigonometry is taught. A typical example is the following for the relationship between speed, distance and time:

  
I’ve expressed my dislike (hatred is perhaps too strong a word) of formula triangles on Twitter before and others have written about them including Stephen Cavadino. Like Stephen my main reason for not being a fan of them is that they are usually introduced as a “trick” for use in particular situations with no reference to the underlying mathematics. 

One of my students when looking at rearranging formulae was asked to make t the subject of an equation and drew a formula triangle as shown below (I’ve re-written it!)  

When I asked why they had drawn a formula triangle they responded “well there are 3 terms so it’s a formula triangle question”. I’ve never seen this misconception before, I guess it is maybe down to formula triangles being used only for 3 term formulae and then this link becoming solidified in the student. 

When I probed a bit further and asked things like “why have you picked 4a to be on the top” after a while they realised their mistake. I can’t help thinking that this wouldn’t have come about if they had never seen a formula triangle and instead had just had plenty of opportunity to practice rearranging formulae. 

Yesterday I went to an Intermediate Geogebra course at the Geogebra Institute of Sheffield run by Mark Dabbs. It  was really good, and I have picked up lots of things I hadn’t realised (but probably should have done). For example, the fact that the input bar can be moved to the top of the screen so that students can more easily see it when projected onto a screen. Or that it is possible to adjust properties of many objects by just highlighting them.

I have lots of ideas of Geogebra things to do, which I’m sure I will post on here as I do them, but I thought I’d quickly share a trick (I’m sure some of you already do this) that gets rid of a little niggle of mine.

When teaching circle theorems I think it is nice to let them have a bit of time to discover them for themselves. With Geogebra you can easily create dynamic worksheets for them to explore. I’ve had a few sheets like the one below for demonstrating the “angle subtended at the centre” theorem

The angle at the centre is obviously meant to be twice the angle at the circumference but \( 2 \times 47.66 = 95.32 \) which is not \(95.31 \). Of course this is just an artefact of the rounding done to represent the angle to two decimal places, but it does distract from what I am hoping the students will spot. This could prompt a nice discussion about rounding errors and limits of accuracy, and of course could be mitigated somewhat by disiplaying more decimal places. But, I had always thought it would be nice if I could restrict the angle at the centre to prevent this from happening – which it turns out is easy to do. Using GeoGebra’s Sequence command (which behaves much like a for loop in a conventional programming language), we can generate a set of points around the circle such that the angle at the centre is either a whole number or a multiple of a half. This means that the angle at the edge will always be exactly represented in the two decimal places restriction.

Once the circle with centre A has been created (by default it is given the name c), I placed one point on the circumference, call it A’ say with the command
[code] A + (Radius[ c],0] [/code]. I then rotated this single point around the circle in increments of  0.5 degrees using the command [code] Sequence[Rotate[A’,kº,A],k,1,360,0.5] [/code]. This rotates the point A’ about the centre of the circle by k degrees in increments of 0.5 degrees, creating a list of points, which by default is named list1. Then  you need to hide the points around the circle from the graphics view, before creating three points B,C and D on the circumference. Once you have added in the appropriate line segments the angle can be added in using the angl tool. The final step is to redefine the definition of the points B, C and D from [code] Point[ c] [/code] to [code] Point[list1] [/code] as shown below in the screen shot from the iPad app – it is much easier to do this in the desktop version.

I have hosted both versions of these basic applets on my website here.

I really would recommnd that anyone who likes using GeoGebra to attend one of Mrk’s courses, it was a great way to spend a few hours and I am hoping to go to the advanced course in July.

Many people came out of this exam saying it was hard, even some of my FM class said they didn’t particularly enjoy it. Compared to the 2014  paper i do think it was a bit harder; the lack of a question concerning the trapezium rule was a noticeable omission of some easy marks. 

Starting on a question by question basis, Question 1 was a straightforward application of the binomial expansion, only requiring 3 terms to be given. This is esppecially easy as you are given the binomial expansion in the formula book! I think this was a very nice start ot the paper and hopefully would have boosted the confidence of the students sitting the paper.

  
Moving on to question 2 we had, what I think, is quite a nice circle geometry question. Finding the equation of the circle is straightforward, given that you are told the centre and a point on the circle  – conceptually I think this is easier the starting part of the equivalent question last year. We then go on to find the equation of a tangent to the circle requiring a bit of memory of circle theorems from GCSE and the properties of perpendicular lines.

Some students that I have spoken to have said that they found Question 3 hard, it is definitely more challenging than the equivalent 2014 question, however it is almost identical to the corresponding question in the 2013 paper. Just use the remainder theorem and factor theorem to form two equations in terms of \(a\) and \(b\) and then solve. It factorises nicely, into the factor given and a differenc of two squares (as long as you recognise that a factor of 3 can be pulled out).

  
The area and perimeter of sectors question (Question 4) seems fairly typical to me, I think some may have found the first part of the question a bit tricky, and won’t have thought to break the triangle into two right angled triangles and then double it. Once the angles have been calculated, completing the rest of the calculation is fairly simple. I guess some may have forgotten to add the base length in when calculating the perimeter. Please marvel at my awful diagram for this question, and note I used the incorrect angle for the last part at first!

  
Question 5 concerned geometric series and to me feels harder than the equivalent question last year. However, as the formulae are all given in the formula book, forming the equations (simultaneous equations again!) required for the first part shouldn’t be too difficult, and solving them drops out nicely.  The second part of this qquestion requires a bit more thought and the use of logarithms to efficiently solve  – I also think a few people will have forgotten to round up to the nearest integer.

   
  
Question 6 moved on to integration and finding the area under a curve. They even gave you the points where the curve crossed the axis and a very helpful picture  of the shaded region to find the area. The tricky part I imagine would be remembering to take the absolute value of the area of the first region when working out the total area.

  
Question 7 was the main logarithm question and I think this was slightly easier than the last two years as it was obviously a logarithm question and no curve sketching was required. As long as students are systematic in their application of the logarithm rules part b should be ok, though there are plenty of places for arithmetic errors to creep in.

 
I think the trigonometry question will have thrown a few people: you don’t often see \(3\theta\) in a question, but apart from that part a is ok as long as they remember the period of \(\tan (3\theta) \)  is a third of that of the period of \(\tan ( \theta) \). The phrasing of part b seems to have confused a few people, but once you have got to a quadratic in \( \cos x \) the solutions drop out nicely. 

The final question was very similar to the last question on the 2014 paper – in that it concerned minimising a function of the surface area of a 3D shape. Minimising it and checking the nature of the stationary point is straightforward and these marks could be picked up even if the candidate hadn’t managed to derive the expression for the cost of polishing themselves.

   
 
 

Overall a nice paper, a bit more challenging than some recent ones in places but generally it seemed pretty fair. They are liking simultaneous equations at the moment.

A scan of the questions is here and a pdf of my solutions (complete with my incorrect attempt of Q5b) available here.

I don’t actually teach Core 1, but as I’m trying to do every A level maths paper sat by students at my school I thought I’d post a few reflections after I had done it. A pdf of my solutions are here respectively.

Overall it seems to have been found pretty easy by the stronger candidates doing Further Mathematics but weaker candidates seem to have found it a bit more difficult. After having done the paper I think that it is fairly straightforward if your algebra skills are good, most questions are clear applications of clearly specified bits of knowledge.

Question 1 was just a bit of manipulation of surds, with the first part used in the second  with quite a nice rationalising the deonominator question. Question 2 was essentially a GCSE qustion – a 7 mark gift to people sitting this exam.  
 

Question 3 was a straightforward test of basic integration and differentiation skills. I think question 4 may have thrown a few people – when I first looked at it I thought I couldn’t do it – but as soon as you do the first part and find a few terms, finding the sum is straightforward. 

 

  Question 5 tests knowledge of the discriminant; I think the fact that the inequality you have to show is a greater than may confuse a few people, and when it comes to finding the set of possible values of p a lot of people will probably apply the quadratic formula instead of completing the square which is (as always) easier.

 
Question 6 is straightforward, nothing challenging there, they just have to do it. Question 7 I like  and is  straight forward when you consider the laws of indices – yet another easy quadratic to factorise. I think the final step may confuse people if they haven’t done something similar before. 

   
 

For Question 8  we have yet another quadratic that factorises (I’m getting a bit bored of these now…), and then a graph to sketch.  I still find it strange that identifying stationary points isn’t in Core 1.

 

Question 9 was a nice application of the formulae for arithmetic progressions. The last part did at least expect some thought on how to calculate the total which made it a bit more interesting.

  
Question 10 was probably the trickiest question, in my opinion, on the paper – the last part is certain to have thrown some people and required more thought than a simple “find the normal” paper. 

  
Overall I thought this was a very fair and accessible paper.