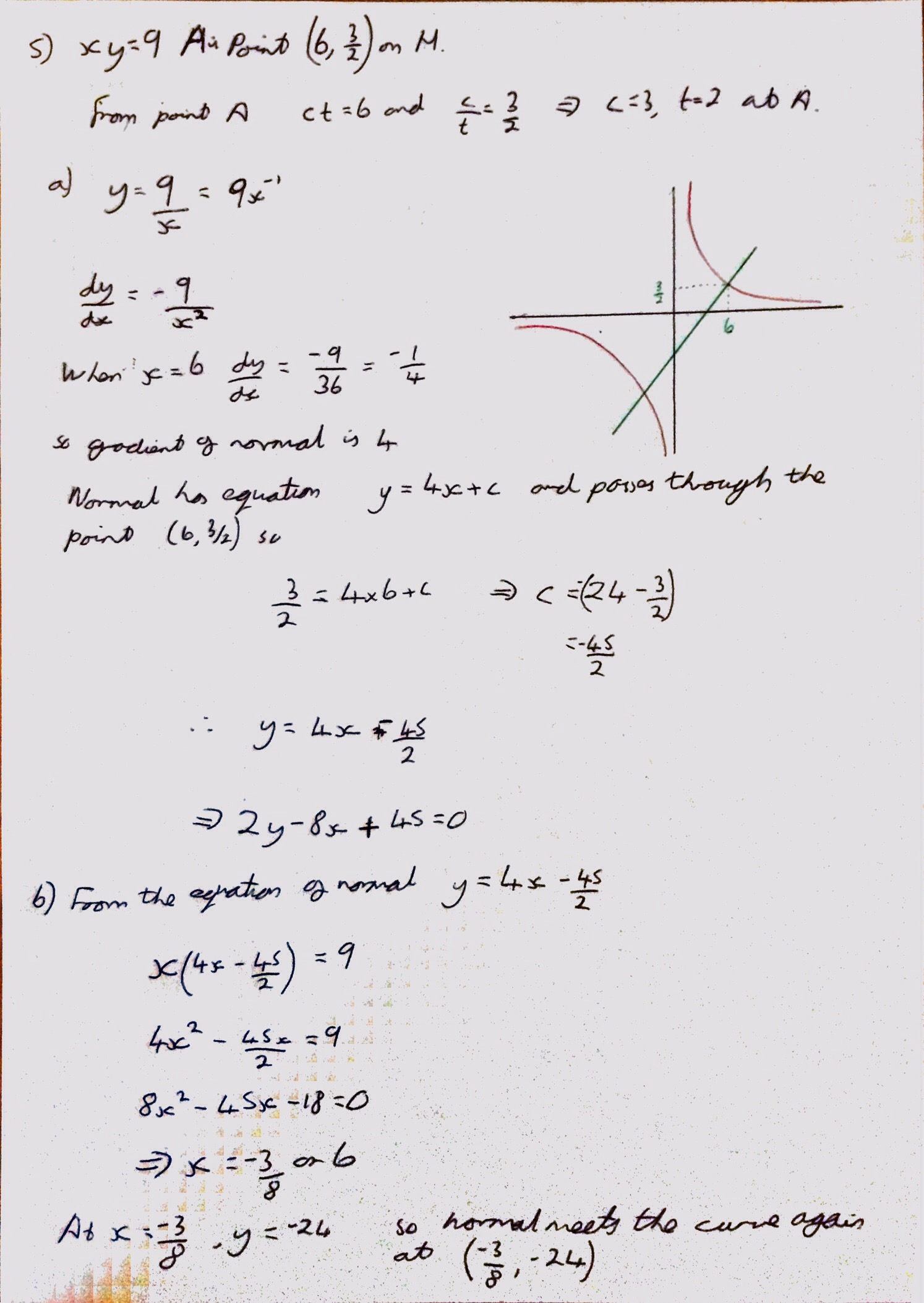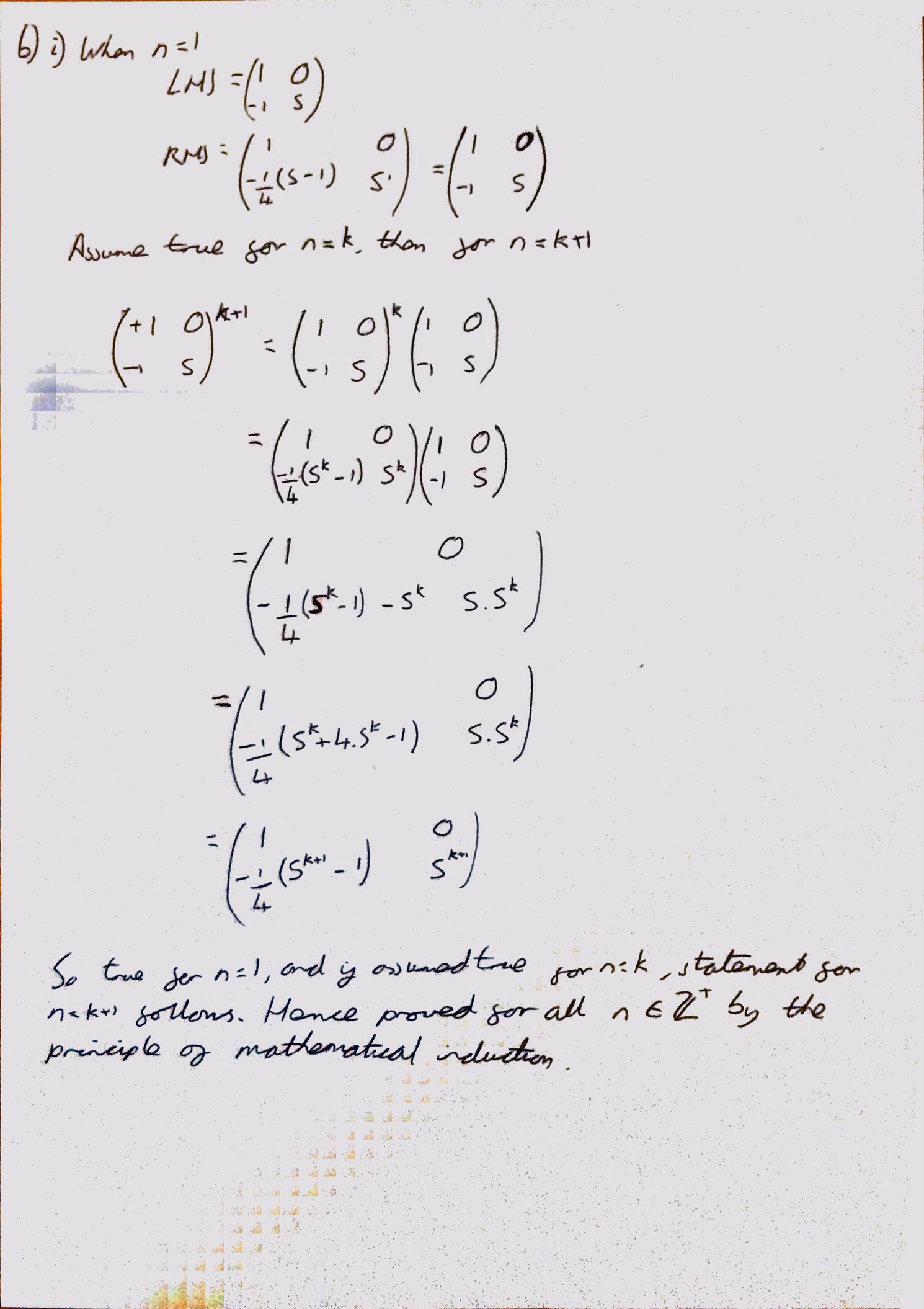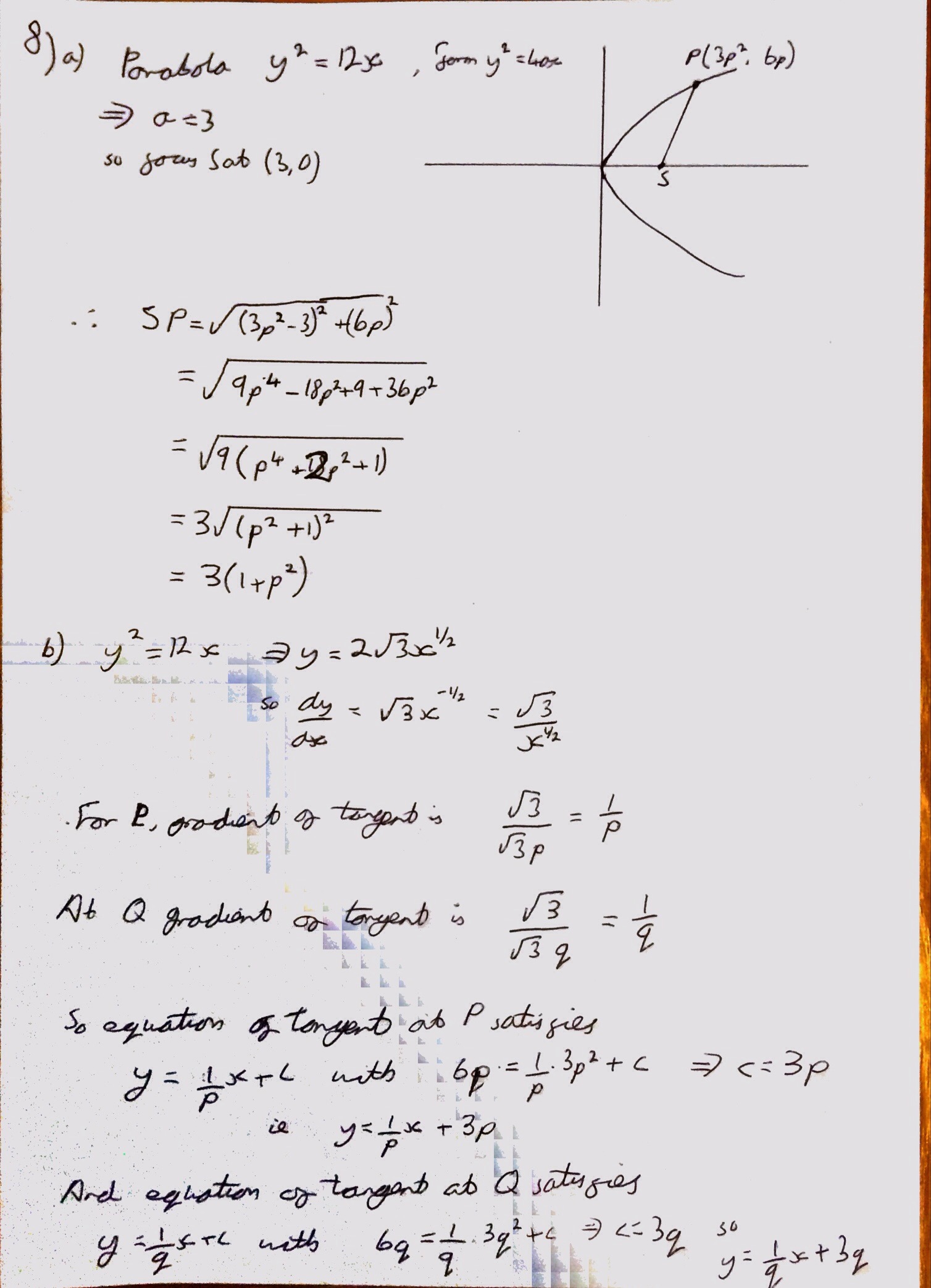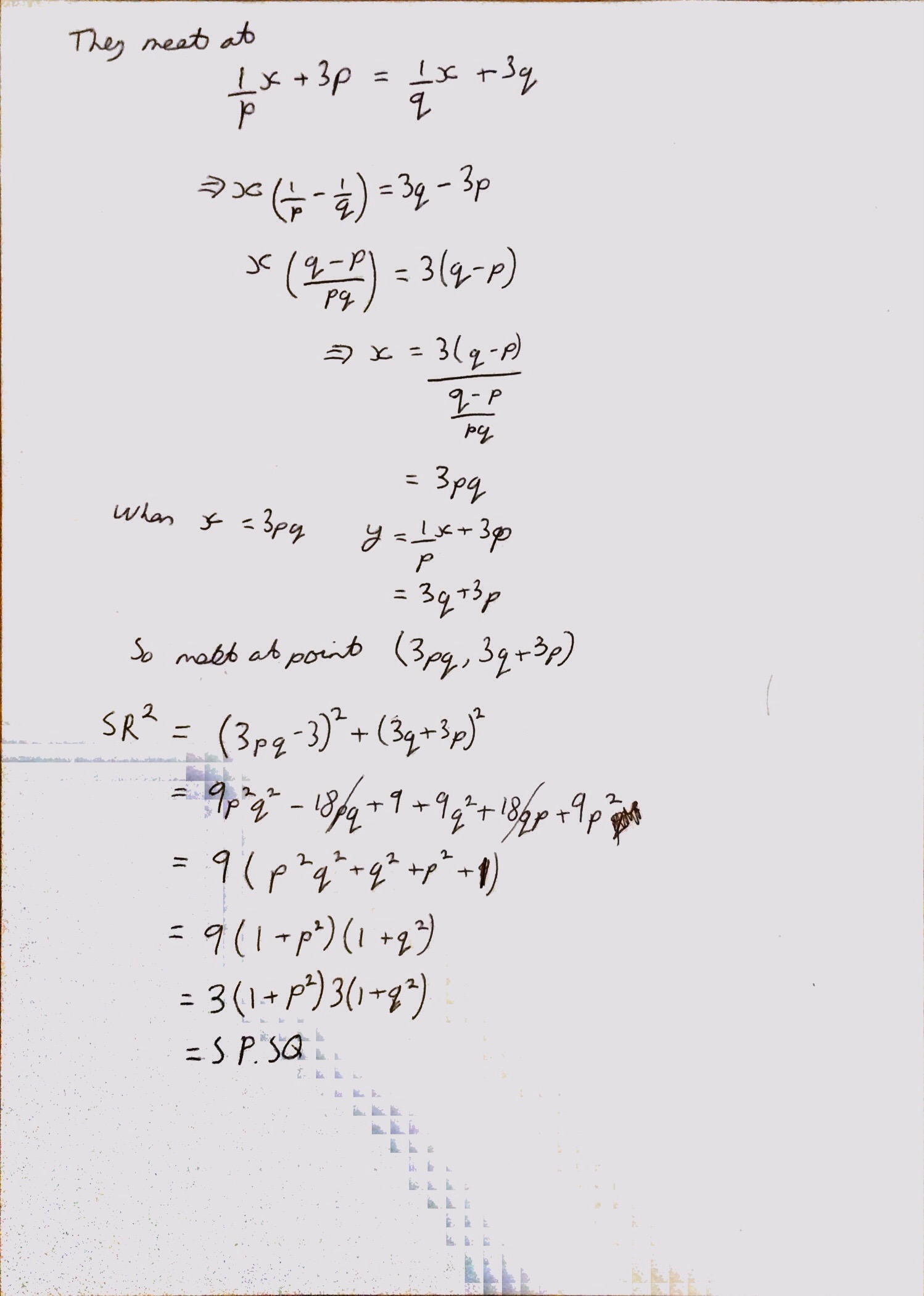Author: tombennison

My students weren’t very happy with this years FP1 exam and found it harder than past papers. After doing the paper, I agree it seems harder than recent past papers but I think it was a fair paper.

Questions 1 and 2 I thought were incredibly straight froward (5 marks for factorising a cubic and solving a quadratic seems generous), though I was surprised and saddened that there was no Newton-Raphson in the numberical-methods section.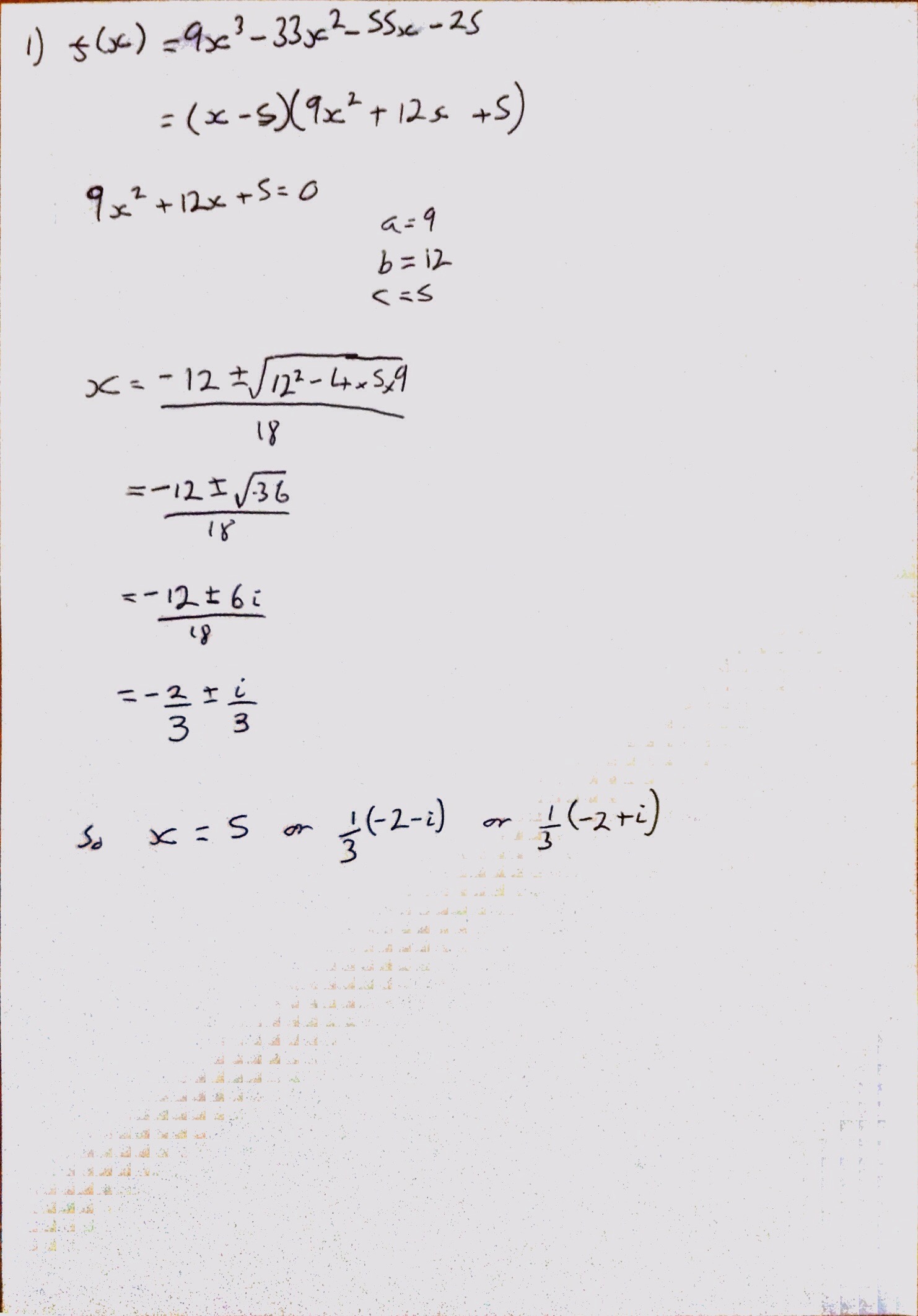  

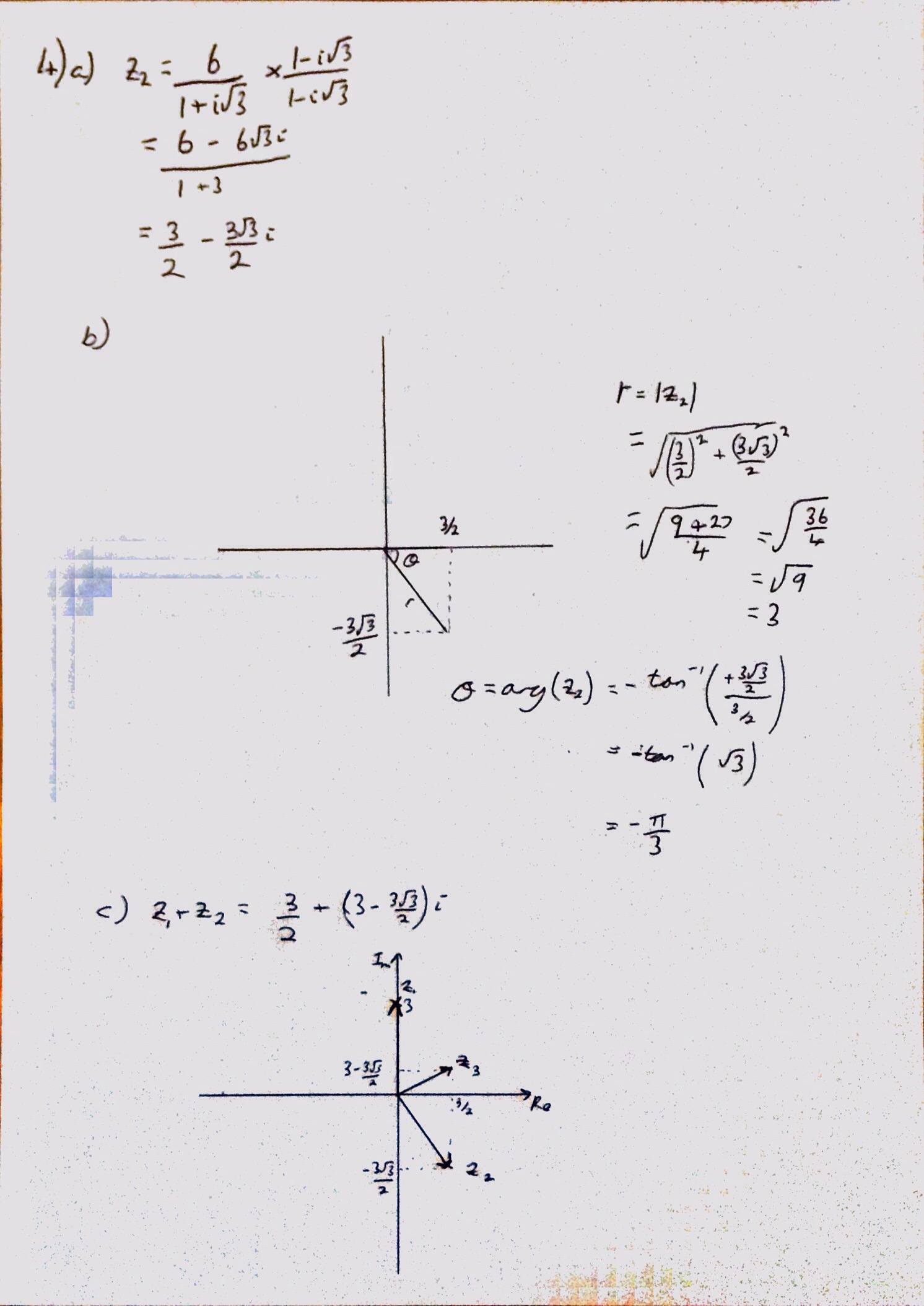
Questions 3 and 4 were nice too, the summations in 3 dropped out quite nicely, and 4 was a straight forward test of basic definitions for complex numbers.

Question 5 concerned the hyperbola, and wasa nice test of the basics of finding normals and points of intersection – not much to trip people up here I didn’t think.

There were two induction proofs for question 6 (no divisibility question though, which everyone I have spoken too seemed pleased about. I feel that these were a bit trickier than similar induction questions in previous years, with the algebraic manipulation to complete step 3 being not as straightforward (in that you couldn’t immediately factorise out some of the terms for the summation proof, for example) as sometimes.

I would describe Question 7 as a gift of a question. I can’t really believe they explicitly asked youto find the inverse of the matrix B, before it needed to be used to work out the coordinates of the triangle T. I think this should eliminate the possibility of candidates using the wrong matrix in this question.

  
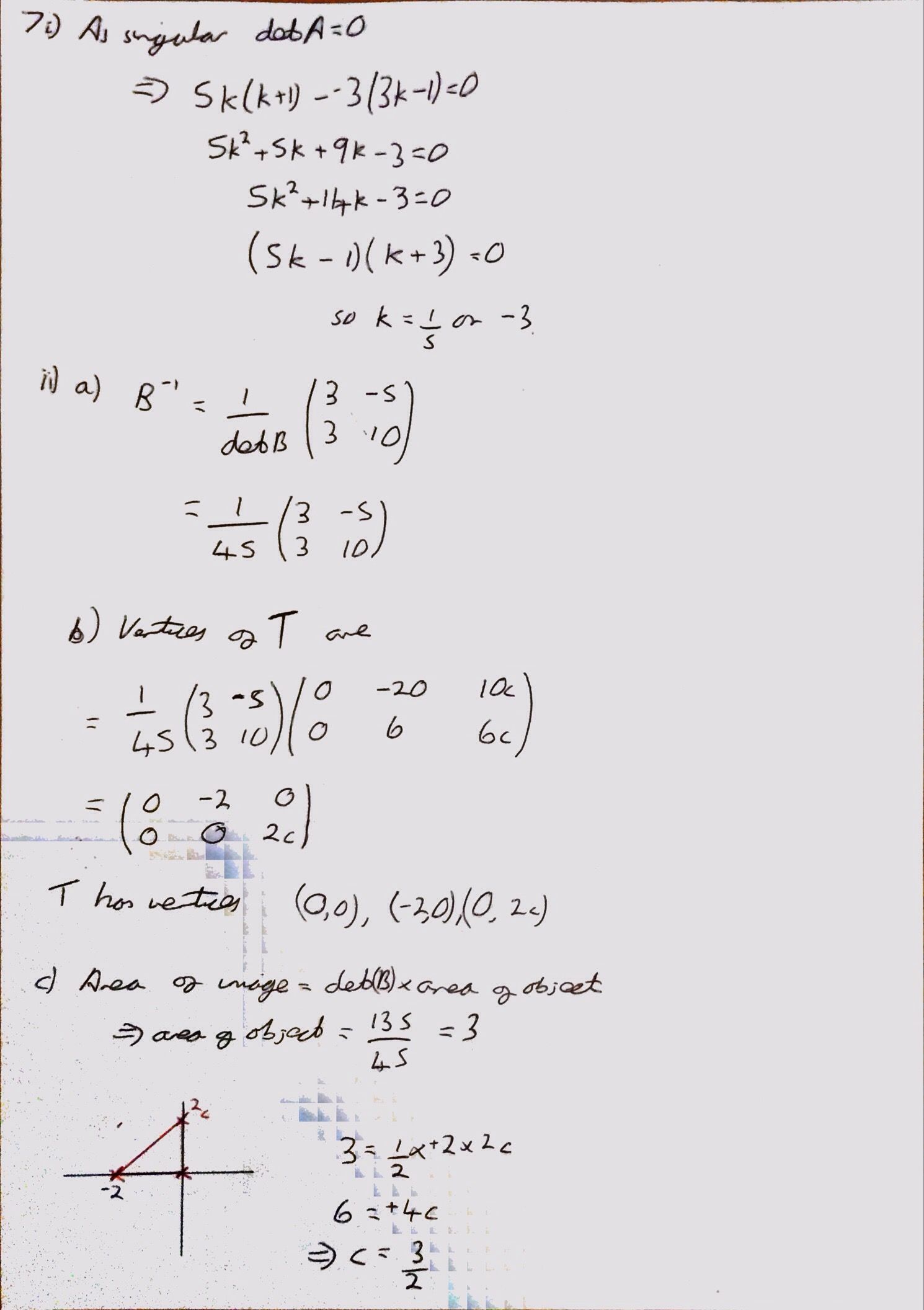
Oddly this paper had only 8 questions, I have got used to the FP1 exam having 9.  The final question was however worth 14 marks and was trickier than a lot of conics questions. I guess the main reason that it seemed trickier was due to the wording of the question and the fact that the last part of the question wasn’t splt into multiple sections. Once you got past the wroding and the similarity of the letters p and q I thought this was quite a satisfying question, and I liked the result you were asked to show in the last part.

Please excuse the strange coloured triangles across the photos, it seems to be an odd artefact of the Office Lens app. 

Update: Click here to download a pdf of my solutions and here for a scan of the questions. 

This post was going to be more involved…. 

Last week a few of us were sharing photos of our collections of maths books and for some reason I couldn’t post more than one photo on a tweet! So, I said I’d write a blog post – I was originally going to write about about some of my favourites, but being short of time tonight I think I will leave that and some of them may make it into my “Classic Maths Books” series. 

My books are seemingly spread all over various book shelves, and some just haven’t made it on to shelves (or I have let people borrow them and when they have come back their shelf space has been taken by something new) so below are photos showing all (I think) of them:

I think I may catalogue them over half term as there are quite a few here I had forgotten that I had…

Are there any that people would recommend I get etc?

I do think it would be good to have a central review of books and some of the nice things they contain or a lending system to spread our collective libraries around. 

This Saturday I went to a great session organised by the East Midland’s branch of the Association of Teachers of Mathematics. It was led by Colin Foster of The University of Nottingham who was talking about “Rich Mahematics from Closed Questions”.

Writing about the session in a no-linear fashion I liked how he used Fermat’s Last Theorem as an example of a yes-no question (often seen as a closed question) leading to rich mathematics.

  
A closed question is often defined as a question with one correct answer and no scope for discussion. The open vs closed question idea is something that is discussed often, with closed questions being seen as inferior to openquestions and not readily leading to rich mathematics.  The aim of this session was to show that rich mathematics can come out of closed questions.

I liked the initial question of \( 15 \times 823 \). This works out to be 12345. I think this could be a nice launch point for a lesson, looking at other similar sums, divisibility rules etc.

Colin then made the point that two closed questions together or a sequence of closed questions can be a good prompt to some interesting maths. He first gave two quadratics \(x^2+7x+6\) and \(2x^2+7x+6\); both of these quadratics can factorise. Then the prompt questions could be things like “Is this a fluke?”, “What can we say about how to make these?”. I confess I haven’t figured this out yet, so will probably write about it when I do.

As an example of a sequence of questions consider the following:

• How many factors does 10 have?
• How many factors does 100 have?
• How many factors does 1000 have?
• How many factors does 10000 have?

I started by manually listing factors, and soon noticed a pattern of the square numbers appearing. It becomes much clearer when you realise that \(10 = 2 \times 5 \), \(100 = (2 \times 5)^2 = 2^2 \times 5^2 \), \( 1000 = 2^3 \times 5^3 \) and so the factors can be computed using a two-way table

  
There are many opportunities for students with this task including practise at finding factors, spotting number patterns, predicting future terms of the sequence, generating nth term rules and investigating how the factors of other sequences grow (for example 6,60,160,1600 and 2,4,8,16,32). Of course not everyone in the class will reach the same point, but this isn’t a problem. I really liked Colin’s justification for doing these kind of activities:

“The emphasis is on the thinking going on in the classroom, not on the kids getting to the final answer” 

This is a nice “low floor, high ceiling” task and I’m going to use it for an observed lesson later this week, and I will blog about the lesson in full towards the end of the week.

I also realised (something that in hindsight I should have known before as it is obvious) that any prime number to the the power of \( n \) has \( n+1 \) factors.
After looking at factors, Colin presented some inequalities to shade (see his paper here for more information – it’s a nice short article!) and a few problems about fitting rectangles into squares.

All in all it was a great session (it was also good to catch up briefly with Rob who is the secretary of the East Midlands Branch) and the £5 cost is a bargain.

It also reinforced the fact that I have always been irritated by the open/closed questioning distinction. An open question can just as much lead to narrow mathematics as a closed question – it’s the questioner (is that a word?!) that is important. 

Today I led the East Midlands West Mathshub Curriculum Development meeting. I had been asked to feedback about the fantastic presentation Jo Morgan (@mathsjem) gave at the last National Mathematics Teachers Conference (mathsconf). Her original presentation is discussed , and her subsequent posts are definitely worth a read.

My presentation is (hopefully) embedded below, and can also be viewed at this link.

[prezi id=”http://prezi.com/zcqk8rt-s0j8/?utm_campaign=share&utm_medium=copy&rc=ex0share” align=center width=600 lock_to_path=1]

It seemed to go well – I was pretty nervous with it being my first presentation to colleagues, all of whom had been teaching for longer than me – and I hope everyone there got something out of it.

I started the presentation with the following analogy that I had recently seen in the book “The Number Sense” by Stanislas Dehaene.

You are given two lists to remember, a personal address book

1. Charlie David lives on George Avenue.
2. Charlie George lives on Albert Zoe Avenue.
3. George Ernie lives on Albert Bruno Avenue.

and a professional address book

1. Charlie David works on Albert Bruno Avenue.
2. Charlie George works on Bruno Albert Avenue.
3. George Ernie works on Charlie Ernie Avenue.

I certainly struggle to remember this list, all the names just get far too confused. However, Stanislas has constructed this in such a way that if you replace the names with numbers then the home and professional addresses represent addition and multiplication facts. I think this is a really nice way of giving a bit of an insight as to why children with numerosity weaknesses confuse multiplication and addition facts.

Jo was kind enough to give me permission to hand out a copy of work book (which received some very positive comments) which I used in conjunction with some slight modifications to a few of her slides.

However, I decided to split the hour and a half (ended up being a bit less due to an Ofsted meeting happening at the University) into two, first of all looking at some software I have used in lessons or for resources, and some techniques I use to stretch the great group of Sixth Formers that I teach. I have been meaning to write blog posts about all of these things if I haven’t already, so hopefully this is the impetus I need to actually do this over the next few weeks – look out for them! I also briefly talked about how I believe that when teaching the numerical methods topics it is important to convey some sort of appreciation for how they would be coded, and pointed people to the post by Manan Shah (@shahlock) where he discussed how to teach programming without a computer.

Following this we looked at a few of the topics that Jo discussed in her talk, and I particularly promoted James Tanton’s website and videos. A while back – last year originally I think – I saw a method for factorising quadratics with leading order coefficients not equal to zero on a blog post by Jo (I really do pick up a lot of interesting things from her posts) and had always been a bit dubious of it. It is called the diamond method (explained in this video) and seemed a bit tricksy to me, but I used it last night during a revision session with some Year 11s who were really struggling with these and they all seemed to pick it up very quickly, and I am told one of them could demonstrate it’s use to another teacher this morning. I’m not sure I would initially teach it in this way, but it certainly seems to have its uses. Many people seemed to like the Indian method for finding out the hcf and lcm.

Please look at the presentation for further details and see the question sheet here. Also check out Jo’s posts on her presentation and topics (factorising, quadratics, highest common factor, sequences, linear graphs and surds) as we covered less than half of them tonight.

Thank you to every one who too the time out during the busy exam season to come tonight. I really enjoyed the conversations I had throughout the session, and it was interesting to see other peoples methods and view points on everything we discussed.

Earlier this week one of my classes said something that I had heard can happen, but hadn’t happened to me yet: 

We were discussing angles in a triangle and I drew a triangle like the one below

  
One of my students then said the fabled “but that isn’t a triangle Sir”. I questioned why they didn’t think it was a triangle and I was told that it “just doesn’t look like a triangle”. We then had a good discussion about what makes defines a triangle, before settling on it being a three sided shape, at which point they accepted the shape I had put on the board was a triangle.

I think this statement highlights the over-use of similar questions. I don’t understand why so many questions in text books have triangles with at least a horizontal base, if not right angled too!

The lesson after I taught matrix multiplication to my FP1 guys I gave them this question as a starter

At first I gave no information of where this came from or how I expected them to solve it. After about 15 minutes had passed, and we had got past the initial “no idea” phase, many of them were solving it by just working out percentage changes of the inter-related statements. I then gave them a hint and said that I would like to see it solved using a matrix. Despite this hint, it was still hard for them to spot that it was a simple matrix multiplication problem. The majority of rose that did spotted it by calculating the final percentage market share for each company in the GCSE sense and then spotting a pattern to their calculations. 

I really like this problem, the students enjoyed it too and said that it made them appreciate the power of matrix multiplication. 

I originally found it on this Discrete Mathematics Project website. It’s worth a look, but this is the only matrix question that seems suitable for A Level. 

Most people I have spoken to aren’t terribly keen on the current A Level textbooks. I think that the current Pearson Edexcel books are particularly poor, worse than the Edexcel books that I had when I was at A Level and definitely not as good as the Bostock and Chandler textbooks that I love. 

I think the questions in the Edexcel books are quite samey, not necessarily challenging enough to stretch the most able and could also highlight links between topics better. The order that they tackle topics is also a bit weird, I can’t work out why the chapter on vectors is at the end of the M1 book for instance. 

I was thinknig that the 100% prescribed A Level course (and 50% prescribed further maths) that is coming in provides a good opportunity to write an exam-board neutral text book / express what we want in a textbook. 

Here is my list of things I would like to see in an A Level textbook:

• A book written in a logical order that highlights the links between topics.
• Rigorous derivations that highlight where methods come from.
• Sections that discuss the use of the mathematics in the real world.
• Plenty of exercises for pupils to practise (with worked solutions available for teachers).
• Scaffolded exercises to develop understanding and pupil’s confidence. 
• Off syllabus sections to help prepare students for university level maths. For example, the Fundamental Theorem of Calculus is something that could be properly discussed at A Level and not just alluded to.
• Access to plenty of virtual manipulatives to demonstrate ideas. These should be accessible to any students that want to use them.
• Links to (free) mathematical software pacakages, especially for investigating data in the statistics sections.
• Explicit emphasis for multiple approaches to solving problems.
• Longer, more free-form questions to challenge students.
• Suggestions for self-study research projects (maybe ones that would be suitable for the EPQ).

I’m really interested to hear what other people would like to see in a text book.? What kind of things do they particularly like/dislike? 

Please comment below or comment on twitter.