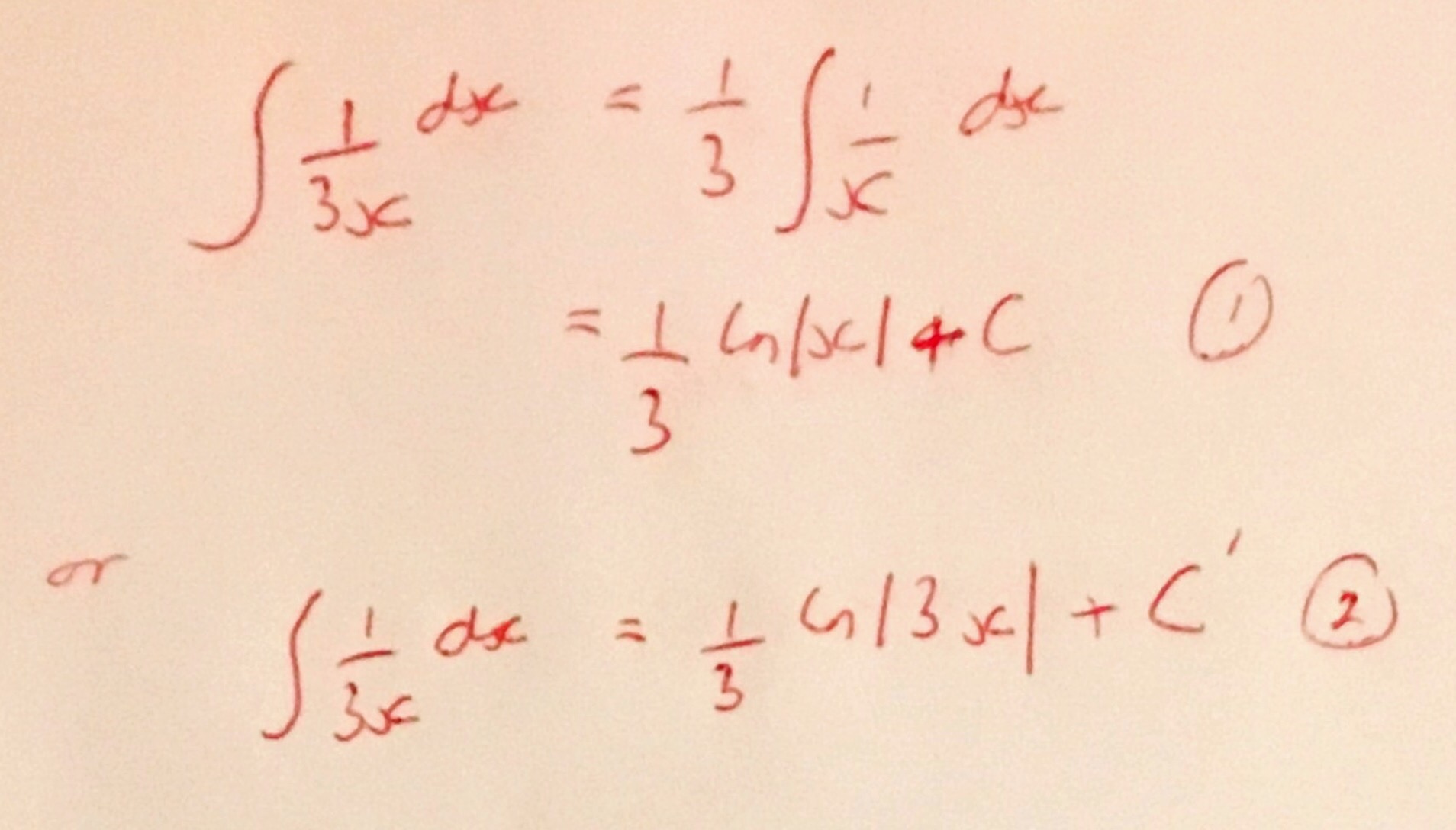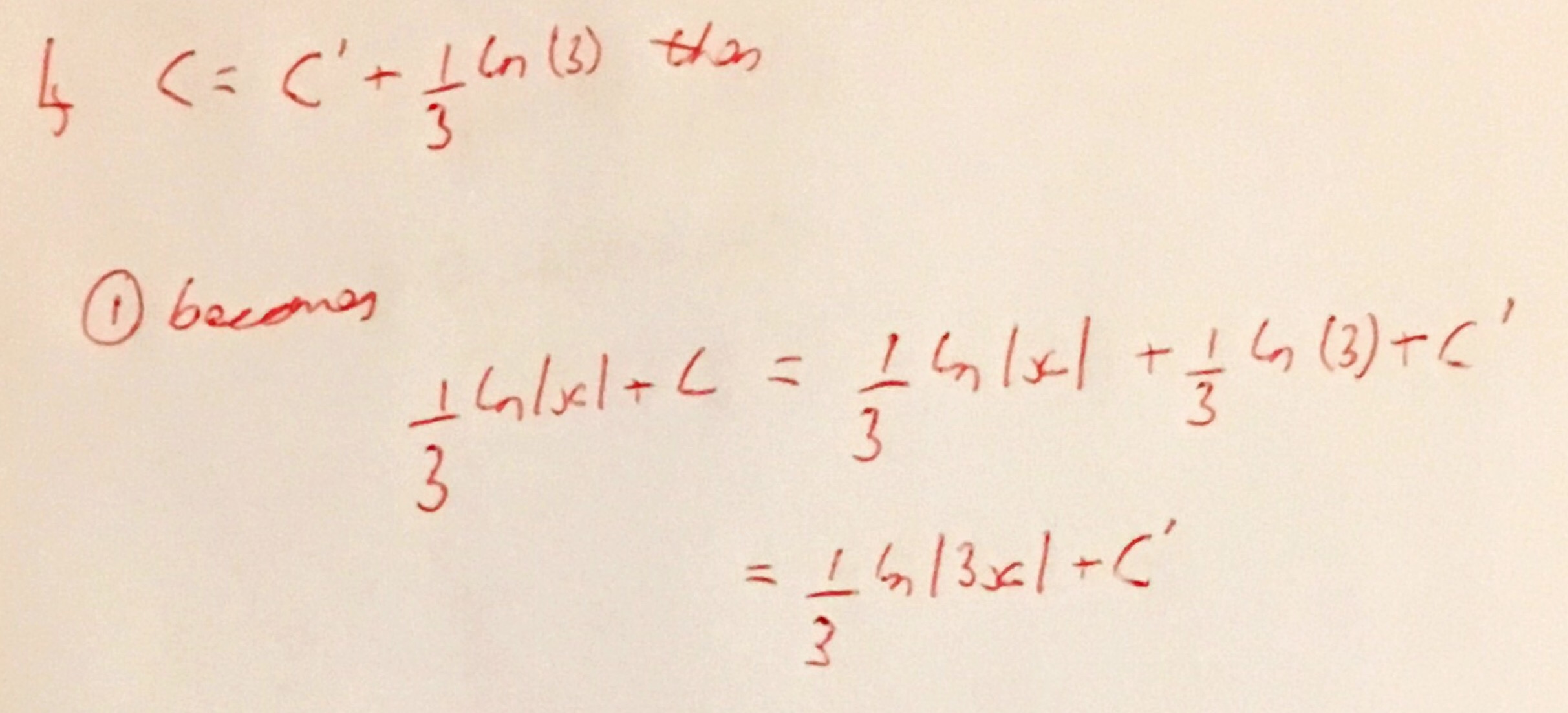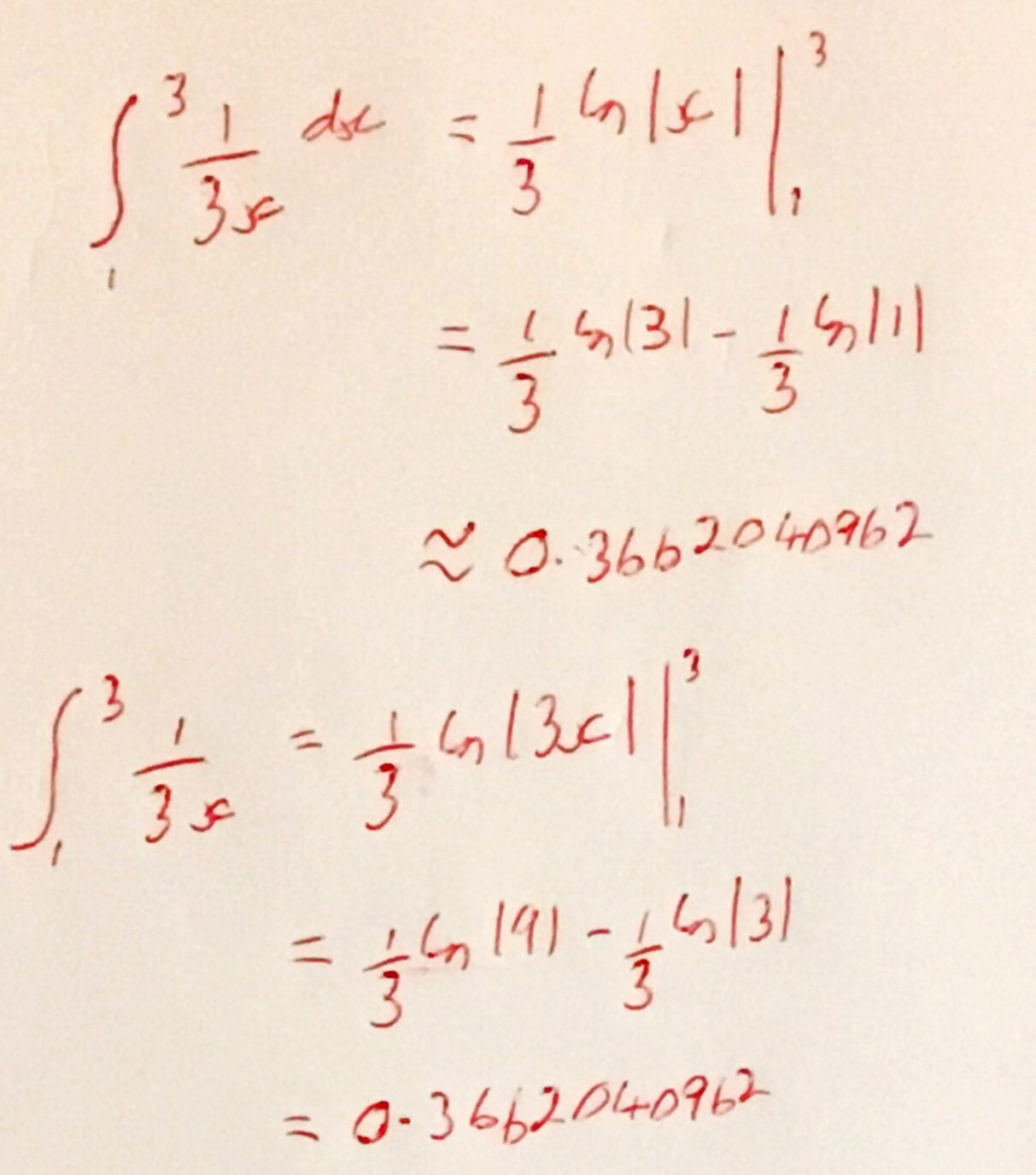Sometimes I find it interesting to think about what kind of maths I could develop out of a given picture. I’m curious to see the kinds of things other people come up with.
What kind of mathematical questions could you pose using the following four pictures as stimuli:
I was recently asked about the integration of \( \frac{1}{3x} \), this had come up in the solution of a differential equation. More specifically the fact that there are multiple ways to integrate this:
At first glance these do not appear to be the same, however plotting them suggests that they are part of the same family of solution curves.
Indeed a simple manipulation of the constant of integration shows them to be the same functions apart from the addition of a constant.
Of course these constants would be fixed by an initial condition, and so both versions of the integration would lead to the same solution of the differential equation.
I have a vague memory of having this confusion myself when I was an A-Level student, but since then I haven’t really thought about this as I always “pull any constants outside of the integral” before integrating.
Thinking about this a bit more, I think that a great question for students would be to ask them to explain why \( [(1/3)\ln (x)]_1^3 = [(1/3)\ln (3x)]_1^3 \). I’m sure many would just evaluate the integrals as shown below, but asking for an explanation could lead to a deep discussion about the nature of the logarithm function.
My Year 11 students have recently sat the Edexcel November 2015 papers as mocks and it was (as ever) interesting to mark these papers and see where they succeeded and where they fell down.
For feedback I have written some questions that are similar to a few questions from these papers, such as the one shown below:
Incase they are useful to anyone the questions corresponding to Paper 1 are here, along with corresponding solutions. The solutions are very rough and ready – please forgive me.
I am a bit late to the party here and despite having fairly recently updated to MATLAB R2016a I have only just noticed that graphics have changed in MATLAB (apparently this happened in release R2014b)!
Among other things the default colour order when plotting multiple functions has changed as has the colormap used in surf. But more excitingly it is now easier to modify things such as axis properties.
For example to produce the graph shown below (and featured in my previous post)
You only need the following few lines of code
Of course it always has been relatively easy to produce plots in MATLAB, the big change is that once I have access to the graphics object i can now use ‘dot’ notation to set properties, much like you would with a structure, or in a general object-oriented programming language. This looks so much cleaner than using the old style set syntax
You can also now easily rotate the tick labels, for example you can modify the above plot to 
using the following simple command
I like these modifications and this has reminded me that I really should stay more up to date with the improvements that each new MATLAB release brings.
While at a meeting yesterday the following question came up due to a student “Why isn’t \(\mathrm{sin}(a+b) = \mathrm{sin}(a) + \mathrm{sin}(b) \sin\)“. My immediate response would be to say “because \(\sin(x)\) isn’t a linear function”, but this isn’t a terribly satisfactory response since the likelihood is that the student doesn’t have a deep understanding of the difference between linear and non-linear functions.
On reflection I think the best explanation is to ask the student to sketch the graph of \(\sin(x)\) and ask them to consider \(\sin(a+b)\) using the graph.Â
It should become clear from the graph that \(\mathrm{sin}(a+b) \) can only be equal to \(\mathrm{sin}(a) + \mathrm{sin}(b)\) when either one of \(a\) or \(b\) is \(360^\circ\) (in fact any multiplicity of the periodicity of \(\sin(x)\).
Another approach could be to ask them to consider a sequence of non-linear functions such as \(f(x)=x^2, f(x) = x^3+3, Â f(x) = 2^x+6\) and ask them to compute \(f(a),f(b),f(a+b)\). This I hope would get rid of the expectation that f(a+b) = f(a)+f(b). The geometric proofs of the true formulae for \(\sin(a+b)\) could be a nice way to close the discussion.
I wonder if this is a consequence of an over-reliance on linear functions for examples of substitution etc in lower school.
As usual Jo Morgan (@mathsjem) has beaten me to it with a great post setting out some of her thoughts concerning the A-Level reforms for Mathematics.
Here are some of my thoughts in a less ordered structure than Jo’s.
I will add to my above thoughts if an when I think of other things to say.
I am looking forward to discussing the A-Level reforms with the other attendees of Stuart’s (@sxpmaths) “Maths in the Sticks” event next month. Preparing for the reforms will also be key content at the “East Midlands KS5 Mathematics Conference 2016” that I am co-organising. Thank you for mentioning this Jo, I hope many people can spare the day to attend during the summer break!
As part of the Edexcel S2 course students study the Poisson distribution (which I have written about in two posts here and here before) and also it’s application as an approximation to the Binomial distribution.
I find that people, most definitely including myself, don’t have an intuitive understanding of how good this approximation is and so I have made a small GeoGebra applet that allows you to explore this for varying values of \(n\) and \(p\). I have embedded it in a webpage on my website and there is a screen shot below.
I’ve found this applet also useful for just exploring the shape of the distributions as you can get a real “feel” for the effect of the probability parameter \(p\).
If you would like to, you can also download the original GeoGebra file.
On Wednesday last week there was an IMA East Midlands Branch talk at Derby University. This talk was organised in conjunction with the British Society for the History of Mathematics (BSHM) and was delivered by Fenny Smith. Fenny has delivered lectures for Gresham College and is an expert in Italian Renaissance algebra. This talk was full of little bits of fascinating information and in this post I hope to share some of them.
It was fascinating to see the accounts from a florentine company’s French branch.
To us – used to Arabic numerals – it was hard to see where the numbers in the accounts were as they were written in Roman numerals. I wasn’t aware of the use of the numeral J to mean the same as I but to also denote the end of a number. Fenny explained that one advantage of our modern number system is the fact that you can check your work, or indeed the work of someone else. If you were using an abacus, the only way you could check your work is to re-do the calculation. This in part explains the adoption of our modern number system.
What we now know as Arabic numerals were developed India, and by the 7th Century were being used by astronomers and mathematicians. They arrived in Baghdad in the late 8th century when Hindu scholars brought their astronomical tables with them.In Baghdad Caliph al-Mansur had a centre of learning, and he didn’t really care where you came from if you had something to contribute you were welcome. We owe a lot of our knowledge of Greek Maths, Philosophy and astronomy to al-Mansur who translated and preserved many Greek works.
Following this the Hindu-Arabic Numerals travelled westwards through the Arabic world towards North Africa and Spain.
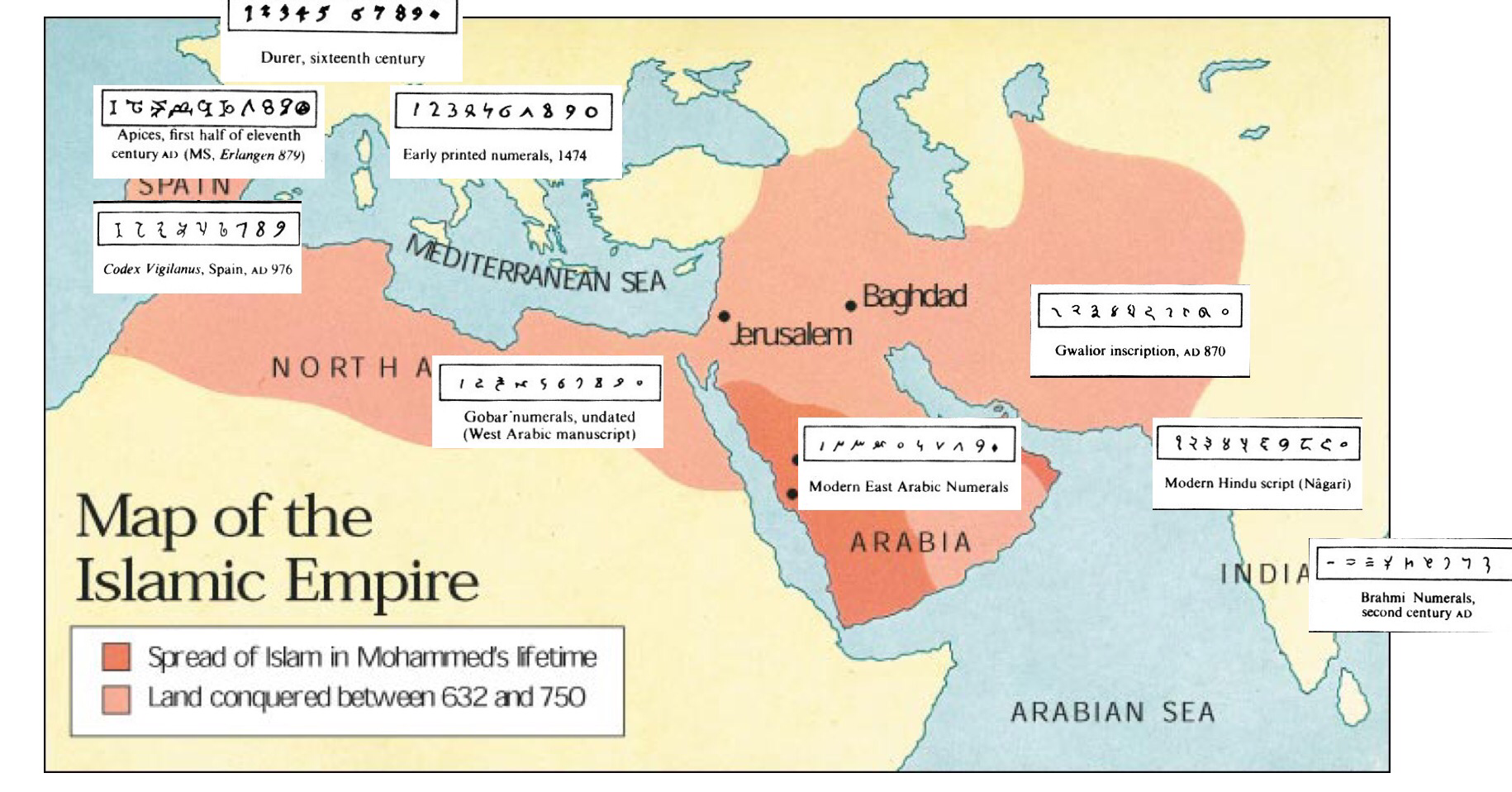In 976 two monks wrote a large manuscript called the Codex Vigilanus and in this they wrote about the new 9 Indo-Arabic numbers. At this point they were seen as curiosities as opposed to something of practical use.
In around 1200 Carmen de Algorismo by Alexander de Villedieu, a popular copy of Dixit Algorizmi (one of the books by Muhammad bin MĆ«sÄ al-KhwÄrizmÄ«, who is often credited with the introduction of Algebra), was published introducing the Arabic numbers to the French. This book was written written in Latin, in rhyming couplets!! This seems pretty impressive to me.
At first there was much resistance and suspicion concerning the new numerals. Fenny explained the suspicion that people had of the concept of zero is to do with our Christian faith where God was said to have created everything, so how could he have created nothing? Conversely in Hinduism nothing is seen as a kind of “nirvana” and so there was no issue with the idea of zero as a placeholder.
The famous engraving Melencolia I by Albrecht DĂŒrer made an appearance during the talk as a demonstration of the development of the numerals too which was interesting.
Another interesting piece of information from this talk is that Gelosia multiplication was so named because he grid structure resembled Venetian window shutters.
It was also interesting to be reminded of Egyptian fractions, which were all unit fractions. An advantage of this representation of fractions that had passed me by, is that it is very easy to compare fractions and decide which is bigger. For example, \(\frac{4}{5} = \frac{1}{2} + \frac{1}{4} + \frac{1}{20}\) and \(\frac{3}{4} = \frac{1}{2} + \frac{1}{4}\) and so it is immediately obvious that \(\frac{4}{5}\) is the larger fraction.
I found learning about the Commercial Revolution was very interesting – a lot of the banking concepts we take for granted now had their origins during this period of time. If you even get a chance to go to a similar talk by Fenny I would encourage you to do so.
I have a recording of the talk, but I have been asked to not share it widely so you will need a password to view the video.
I am really enjoying having a great PGCE student (@MrPullenMaths) in some of my Year 12 Further Maths lessons. (He isn’t massively active on Twitter at the moment so please follow him and welcome him!) He has recently been teaching the Poisson distribution and on Monday this week discussed using the Poisson distribution as an approximation to the binomial distribution. He knows that I like to delve a bit further (and maybe more rigorously) into the maths with my classes and so he looked at the proof of the validity of this approximation. I would probably have avoided this as it is quite technical, however it went really well and I was particularly impressed as this wasn’t in his lesson plan and he ad-libbed the proof. He asked for assistance a couple of times, but I actually think this improved the presentation as it became more of a discussion with everyone in the room than just a “work through of the proof”. A shot of the board is shown below:
In future I think there are a couple of aspects that can be improved, just by tweaking the layout to emphasise a few points:
This lesson made me realise that even though I have very high expectations of my students I am sometimes guilty of limiting the mathematics I expose them too.
Finally, give @MrPullenMaths a follow on Twitter and encourage him to be more active.
Recently I have been covering hypothesis tests with both my Year 12 and Year 13 further maths groups and I noticed differing wordings in exam mark schemes (Edexcel S2).
I’ve always taught that you cannot say “we accept \(H_0\)” as you can’t prove that \(H_0\) is correct, and that you should say something like “There is insufficient evidence to reject \(H_0\)“. However, as the example below from January 2013 shows they seem to be happy with you saying “accept \(H_0\)“:
January 2013
But strangely they don’t always use this language:
May 2011
I’m interested – how do you teach it?